1.2　函数及其表示

30

CHAPTER 1

1.2 函数及其表示

1.2.1 函数的概念

在初中我们已经学习过函数的概念，并且知道可以用函数描述变量之间的依赖关系。现在我们将进一步学习函数及其构成要素，下面先看几个实例。

(1) 一枚炮弹发射后，经过 26 s 落到地面击中目标，炮弹的射高为 845 m，且炮弹距地面的高度 h (单位：m) 随时间 t (单位：s) 变化的规律是

h = 130t - 5t² (*)

这里，炮弹飞行时间的变化范围是数集 A = {t | 0 ≤ t ≤26}，炮弹距地面的高度的变化范围是数集 B = {h | 0 ≤ h ≤ 845}。从问题的实际意义可知，对于数集 A 中的任意一个时间 t，按照对应关系 (*)，在数集 B 中都有唯一确定的高度 h 和它对应。

(2) 近几十年来，大气层中的臭氧迅速减少，因而出现了臭氧层空洞问题。图 1.2-1 中的曲线显示了南极上空臭氧图1.2-1的面积。

17

31

CHAPTER

普通高中课程标准实验教科书 数学 1

层空洞的面积从1979~2001年的变化情况。

根据图1.2-1中的曲线可知，时间的变化范围是数集
A={t | 1979<t≤2001}，臭氧层空洞面积S的变化范围是数集
B={S | 0<S≤26}，并且，对于数集A中的每一个时刻，按照图中曲线，在数集B中都有唯一确定的臭氧层空洞面积S和它对应。

(3)国际上常用恩格尔系数反映一个国家人民生活质量的高低，恩格尔系数越低，生活质量越高。表1-1中恩格尔系数随时间(年)变化的情况表明，“八五”计划以来，我国城镇居民的生活质量发生了显著变化。

表1-1 “八五”计划以来我国城镇居民恩格尔系数变化情况

时间(年)	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000	2001
城镇居民家庭恩格尔系数(%)	53.8	52.9	50.1	49.9	49.9	48.6	46.4	44.5	41.9	39.2	37.9

请你仿照(1)(2)描述表1-1中恩格尔系数和时间(年)的关系。

分析、归纳以上三个实例，它们有什么共同点？

归纳以上三个实例，我们看到，三个实例中变量之间的关系都可以描述为：对于数集A中的每一个x，按照某种对应关系f，在数集B中都有唯一确定的y和它对应，记作
f: A→B.

一般地，我们有：

设A、B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数 f(x) 和它对应，那么就称f: A→B为从集合A到集合B的一个函数(function)，记作
y=f(x), x∈A.

18

32

第一章 集合与函数概念

第一章

其中，x叫做自变量，x的取值范围A叫做函数的定义域(domain)；与x的值相对应的y值叫做函数值，函数值的集合{f(x)|x∈A}叫做函数的值域(range).

我们所熟悉的一次函数y=ax+b(a≠0)的定义域是R，值域也是R.对于R中的任意一个数x，在R中都有唯一的数y=ax+b(a≠0)和它对应。

二次函数y=ax²+bx+c(a≠0)的定义域是R，值域是B.当a>0时，B = {$y|y\ge \frac{4ac-b^2}{4a}$};当a<0时，B = {$y|y\le \frac{4ac-b^2}{4a}$}.对于R中的任意一个数x，在B中都有唯一的数y=ax²+bx+c(a≠0)和它对应。

反比例函数y=$\frac{k}{x}$(k≠0)的定义域、对应关系和值域各是什么？请用上面面的函数定义描述这个函数。

思考

研究函数时常会用到区间的概念。

设a, b是两个实数，而且a<b. 我们规定：

(1) 满足不等式a≤x≤b的实数的集合叫做闭区间，表示为[a, b]；

(2) 满足不等式a<x<b的实数的集合叫做开区间，表示为(a, b)；

(3) 满足不等式a≤x<b或a<x≤b的实数的集合叫做半开半闭区间，分别表示为[a, b), (a, b].

这里的实数a与b都叫做相应区间的端点。

定义	名称	符号	数轴表示
{$x	a\le x\le b$}	闭区间	[a, b]
{$x	a<x<b$}	开区间	(a, b)
{$x	a\le x<b$}	半开半闭区间	[a, b)
{$x	a<x\le b$}	半开半闭区间	(a, b]

19

33

CHAPTER 1

普通高中课程标准实验教科书 数学 1

这些区间的几何表示如上表所示。在图中，用实心点表示包括在区间内的端点，用空心点表示不包括在区间内的端点。

实数集 R 可以用区间表示为 ($-\infty$, $+\infty$)，“$\infty$”读作“无穷大”, “$-\infty$”读作“负无穷大”, “$+\infty$”读作“正无穷大”。我们可以把满足 $x \ge a$, $x > a$, $x \le b$, $x < b$ 的实数 x 的集合分别表示为 $[a, +\infty)$, $(a, +\infty)$, $(-\infty, b]$, $(-\infty, b)$。

例 1

已知函数 $f(x) = \sqrt{x+3} + \frac{1}{x+2}$

(1) 求函数的定义域；

(2) 求 $f(-3)$, $f(\frac{2}{3})$ 的值；

(3) 当 $a \ge 0$ 时，求 $f(a)$, $f(a-1)$ 的值。

分析：函数的定义域通常由问题的实际背景确定，如前所述的三个实例，如果只给出解析式 $y = f(x)$，而没有指明它的定义域，那么函数的定义域就是指能使这个式子有意义的实数的集合。

解：(1) 使根式 $\sqrt{x+3}$ 有意义的实数 x 的集合是 $\{x | x \ge -3\}$，使分式 $\frac{1}{x+2}$ 有意义的实数 x 的集合是 $\{x | x \ne -2\}$。所以，这个函数的定义域就是

$\{x | x \ge -3\} \cap \{x | x \ne -2\} = \{x | x \ge -3, x \ne -2\}$。

(2) $f(-3) = \sqrt{-3+3} + \frac{1}{-3+2} = -1$;

$f(\frac{2}{3}) = \sqrt{\frac{2}{3}+3} + \frac{1}{\frac{2}{3}+2} = \sqrt{\frac{11}{3}} + \frac{3}{8} = \frac{3}{8} + \frac{\sqrt{33}}{3}$

(3) 因为 $a \ge 0$，所以 $f(a)$, $f(a-1)$ 有意义。

$f(a) = \sqrt{a+3} + \frac{1}{a+2}$；

$f(a-1) = \sqrt{a-1+3} + \frac{1}{(a-1)+2} = \sqrt{a+2} + \frac{1}{a+1}$

由函数的定义可知，一个函数的构成要素为：定义域，

20

34

第一章 集合与函数概念

对应关系和值域，由于值域是由定义域和对应关系决定的，所以，如果两个函数的定义域和对应关系完全一致，我们就称这两个函数相等。

例2 下列函数中哪个与函数y=x相等？

(1) y=(√x)²; (2) y=√x²;
(3) y=√x²; (4) y=x/x;

解:

(1) y=(√x)²=x (x≥0), 这个函数与函数y=x(x∈R)虽然对应关系相同，但是定义域不相同，所以，这个函数与函数y=x(x∈R)不相等。

(2) y=√x²=x (x∈R), 这个函数与函数y=x(x∈R)不仅对应关系相同，而且定义域也相同，所以，这个函数与函数y=x(x∈R)相等。

(3) y=√x²=|x|={x, x≥0;
-x, x<0}, 这个函数与函数y=x(x∈R)的定义域都是实数集R，但是当x<0时，它的对应关系与函数y=x (x∈R)不相同，所以，这个函数与函数y=x(x∈R)不相等。

(4) y=x/x的定义域是{x|x≠0}，与函数y=x(x∈R)的对应关系相同但定义域不相同，所以，这个函数与函数y=x(x∈R)不相等。

至此，我们在初中学习的基础上，运用集合和对应的语言刻画了函数概念，并引进了符号y=f(x)，明确了函数的构成要素，比较两个函数定义，你对函数有什么新的认识？

21

35

第 一 章 练习

1. 求下列函数的定义域：
   (1) $f(x) = \frac{1}{4x + 7}$
   (2) $f(x) = \sqrt{1 - x} + \sqrt{x + 3} - 1$

2. 判断下列各组中的函数是否相等，并说明理由：
   (1) 表示导弹飞行高度与时间关系的函数 $h = 500t - 5t^2$ 和二次函数 $y = 500x - 5x^2$；
   (2) $f(x) = 1$ 和 $g(x) = x^2$

3. 已知函数 $f(x) = 3x^2 + 2x$，
   (1) 求 $f(2)$、$f(-2)$、$f(2) + f(-2)$ 的值；
   (2) 求 $f(a)$、$f(-a)$、$f(a) + f(-a)$ 的值；
   (3) 你从 (2) 中发现了什么结论？

1.2.2 函数的表示法

我们在初中已经接触过函数的三种表示法：解析法、图象法和列表法。

解析法，就是用数学表达式表示两个变量之间的对应关系，如 1.2.1 的实例 (1)。

图象法，就是用图象表示两个变量之间的对应关系，如 1.2.1 的实例 (2)。

列表法，就是列出表格来表示两个变量之间的对应关系，如 1.2.1 的实例 (3)。

例 3 某种笔记本的单价是 5 元，买 $x$ ($x \in \{1, 2, 3, 4, 5\}$) 个笔记本需要 $y$ 元，试用函数的三种表示法表示函数 $y = f(x)$。

解：这个函数的定义域是数集 $\{1, 2, 3, 4, 5\}$。

用解析法可将函数 $y = f(x)$ 表示为

$y = 5x$, $x \in \{1, 2, 3, 4, 5\}$

用列表法可将函数 $y = f(x)$ 表示为

笔记本数 x	1	2	3	4	5
钱数 y	5	10	15	20	25

36

第一章 集合与函数概念

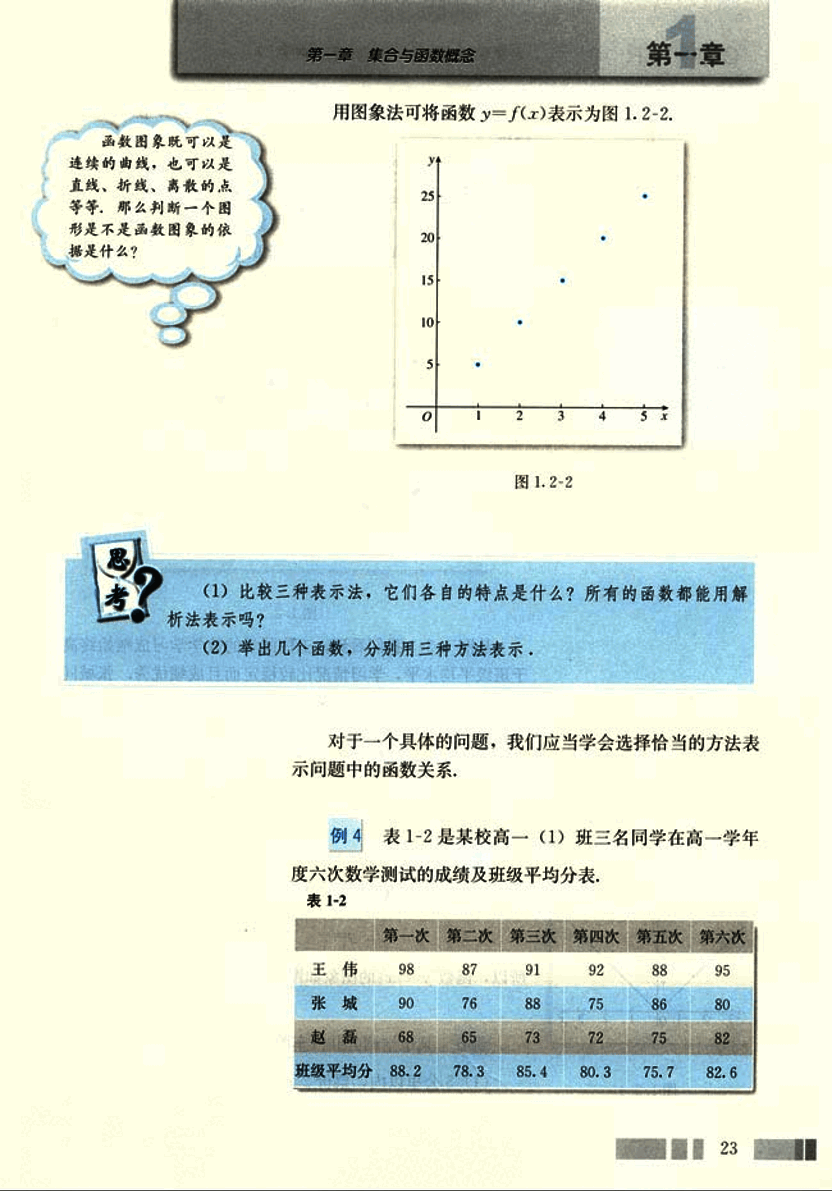
用图象法可将函数 y=f(x) 表示为图 1.2-2.

image

图 1.2-2

(1) 比较三种表示法，它们各自的特点是什么？所有的函数都能用解析法表示吗？

(2) 举出几个函数，分别用三种方法表示。

对于一个具体的问题，我们应当学会选择恰当的方法表示问题中的函数关系。

例 4 表 1-2 是某校高一 (1) 班三名同学在高一学年年度六次数学测试的成绩及班级平均分表。

表 1-2

	第一次	第二次	第三次	第四次	第五次	第六次
王伟	98	87	91	92	88	95
张城	90	76	88	75	86	80
赵磊	68	65	73	72	75	82
班级平均分	88.2	78.3	85.4	80.3	75.7	82.6

23

37

CHAPTER 1

请你对这三位同学在高一学年度的数学学习情况做一个分析.

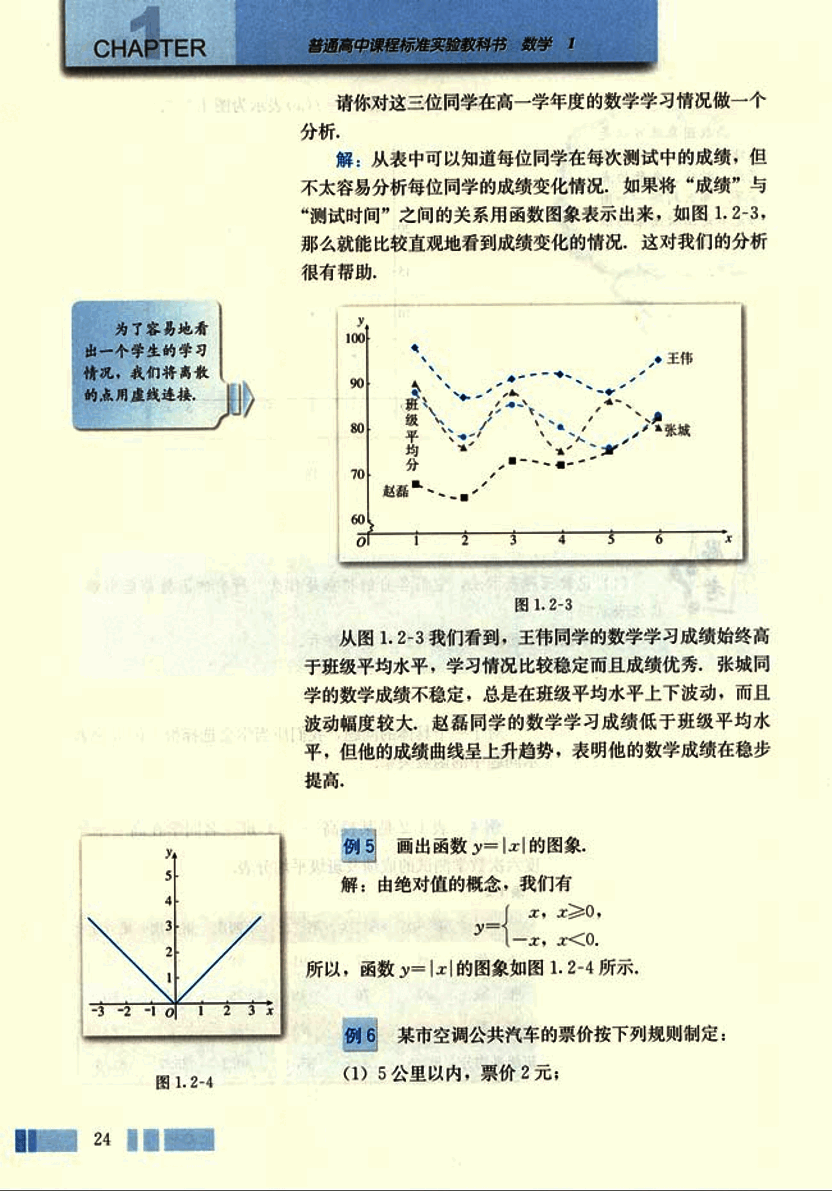
解: 从表中可以知道每位同学在每次测试中的成绩，但不太容易分析每位同学的成绩变化情况。如果将“成绩”与“测试时间”之间的关系用函数图象表示出来，如图1.2-3，那么就能比较直观地看到成绩变化的情况，这对我们的分析很有帮助。

为了容易地看出一个学生的学习情况，我们将离散的点用虚线连接。

image

从图1.2-3我们看到，王伟同学的数学学习成绩始终高于班级平均水平，学习情况比较稳定而且成绩优秀；张城同学的数学成绩不稳定，总是在班级平均水平上下波动，而且波动幅度较大；赵磊同学的数学学习成绩低于班级平均水平，但他的成绩曲线呈上升趋势，表明他的数学成绩在稳步提高。

例 5

画出函数 $y=|x|$ 的图象.

解: 由绝对值的概念，我们有

$y = \begin{cases} x, & x \ge 0 \\ -x, & x < 0 \end{cases}$

所以，函数 $y=|x|$ 的图象如图1.2-4所示.

image

例 6

某市空调公共汽车的票价按下列规则制定:

(1) 5公里以内，票价2元;

24

38

第一章 集合与函数概念

第一章

(2) 5公里以上，每增加5公里，票价增加1元（不足5公里的按5公里计算）。

已知两个相邻的公共汽车站间相距约为1公里，如果沿途（包括起点站和终点站）有21个汽车站，请根据题意，写出票价与里程之间的函数解析式，并画出函数的图像。

解：设票价为y，里程为x，则根据题意，

如果某空调汽车运行路线中设21个汽车站，那么汽车行驶的里程约为20公里，所以自变量x的取值范围是(0，20]。

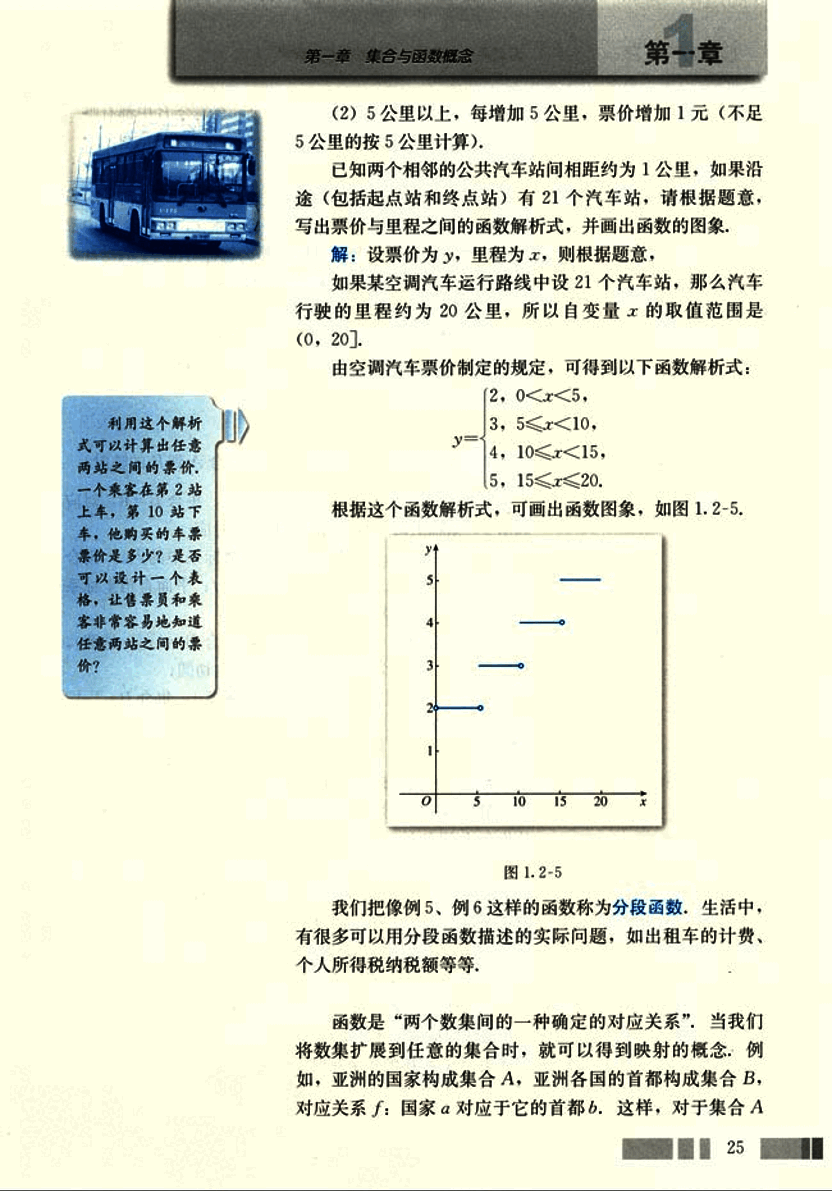
由空调汽车票价制定的规定，可得到以下函数解析式：

$y=\begin{cases} 2, & 0<x<5, \\ 3, & 5\leq x<10, \\ 4, & 10\leq x<15, \\ 5, & 15\leq x\leq20. \end{cases}$

根据这个函数解析式，可画出函数图像，如图1.2-5。

图1.2-5

我们把像例5、例6这样的函数称为分段函数，生活中，有很多可以用分段函数描述的实际问题，如出租车的计费、个人所得税纳税额等等。

函数是“两个数集间的一种确定的对应关系”，当我们将数集扩展到任意的集合时，就可以得到映射的概念，例如，亚洲的国家构成集合A，亚洲各国的首都构成集合B，对应关系f：国家对应于它的首都。这样，对于集合A

39

CHAPTER 1

普通高中课程标准实验教科书 数学 1

在集合B中都有唯一确定的首都与之对应，我们将对应f:A→B称为映射。

一般地，我们有：

设A，B是两个非空的集合，如果按某一个确定的对应关系f，使对于集合A中的任意一个元素x，在集合B中都有唯一确定的元素y与之对应，那么就称对应f:A→B为从集合A到集合B的一个映射(mapping)。

在我们的生活中，有很多映射的例子，例如，设集合A={x|x是某场电影票上的号码}，集合B={x|x是某电影院的座位号}，对应关系f:电影票的号码对应于电影院的座位号，那么对应f:A→B是一个映射。

例 7 以下给出的对应是不是从集合A到B的映射？

(1) 集合A={P|P是数轴上的点}，集合B=R，对应关系f:数轴上的点与它所代表的实数对应；

(2) 集合A={P|P是平面直角坐标系中的点}，集合B={(x, y)|x∈R, y∈R}，对应关系f:平面直角坐标系中的点与它的坐标对应；

(3) 集合A={x|x是三角形}，集合B={x|x是圆}，对应关系f:每一个三角形都对应它的内切圆；

(4) 集合A={x|x是新华中学的班级}，集合B={x|x是新华中学的学生}，对应关系f:每一个班级都对应班里的学生。

解：

(1) 按照建立数轴的方法可知，数轴上的任意一个点，都有唯一的实数与之对应，所以这个对应f:A→B是从集合A到B的一个映射。

(2) 按照建立平面直角坐标系的方法可知，平面直角坐标系中的任意一个点，都有唯一的一个实数对与之对应，所以这个对应f:A→B是从集合A到B的一个映射。

(3) 由于每一个三角形只有一个内切圆与之对应，所以这个对应f:A→B是从集合A到B的一个映射。

(4) 新华中学的每一个班级里的学生都不止一个，即与一个班级对应的学生不止一个，所以这个对应f:A→B不是从集合A到B的一个映射。

26

40

第一章 集合与函数概念

思考

对于例7,如果将(3)中的对应关系f改为:每一个圆都对应它的内接三角形;(4)中的对应关系f改为:每一个学生都对应它的班级,那么对应f:B→A是从集合B到A的映射吗?

练习

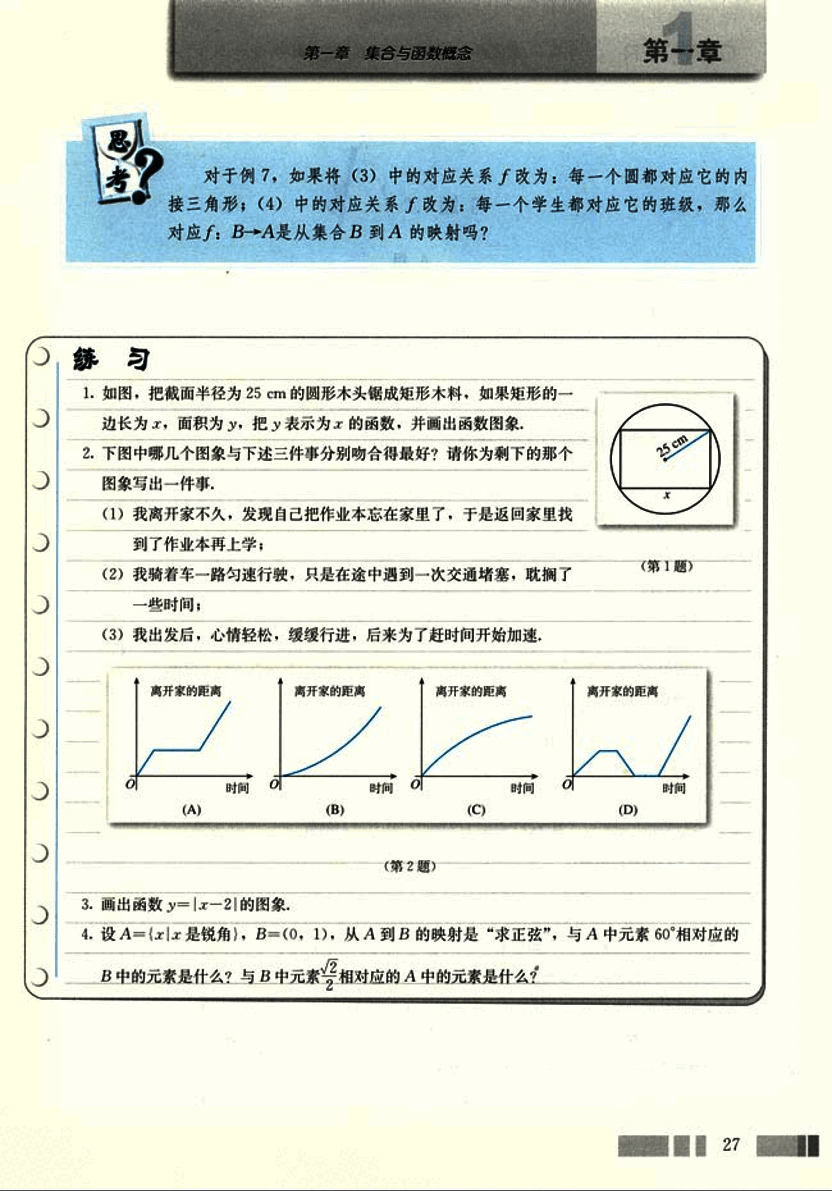
1. 如图,把截面半径为25cm的圆形木头锯成矩形木料,如果矩形的一边长为x,面积为y,把y表示为x的函数,并画出函数图象。

image1

2. 下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写出一件事。

(1) 我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;

(2) 我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;

(3) 我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。

image2

3. 画出函数 $y=|x-2|$ 的图象.

4. 设 $A=\{x|x是锐角\}$, $B=(0,1)$, 从A到B的映射是“求正弦”,与A中元素60°相对应的B中的元素是什么?与B中元素$\frac{\sqrt{2}}{2}$相对应的A中的元素是什么?

27

41

CHAPTER 1

习题 1.2 / A组

1. 求下列函数的定义域：
   (1) $f(x) = \frac{3x}{x-4}$
   (2) $f(x) = \sqrt{x}$
   (3) $f(x) = x^2 - 3x + 2$
   (4) $f(x) = \frac{\sqrt{4-x}}{x-1}$

2. 下列哪一组中的函数 $f(x)$ 与 $g(x)$ 相等？
   (1) $f(x) = x - 1$, $g(x) = x - 1$;
   (2) $f(x) = x^2$, $g(x) = (\sqrt{x})^2$;
   (3) $f(x) = x^2$, $g(x) = \sqrt{x^2}$

3. 画出下列函数的图象，并说出函数的定义域、值域：
   (1) $y = 3x$;
   (2) $y = \frac{8}{x}$;
   (3) $y = -4x + 5$;
   (4) $y = x^2 - 6x + 7$.

4. 已知函数 $f(x) = 3x^2 - 5x + 2$，求 $f(-\sqrt{2})$，$f(-a)$，$f(a+3)$，$f(a) + f(3)$ 的值.

5. 已知函数 $f(x) = \frac{x+2}{x-6}$:
   (1) 点 $(3, 14)$ 在 $f(x)$ 的图象上吗？
   (2) 当 $x = 4$ 时，求 $f(x)$ 的值；
   (3) 当 $f(x) = 2$ 时，求 $x$ 的值.

6. 若 $f(x) = x^2 + bx + c$，且 $f(1) = 0$，$f(3) = 0$，求 $f(-1)$ 的值.

7. 画出下列函数的图象：
   (1) $F(x) = \begin{cases} 0, & x \le 0 \\ 1, & x > 0 \end{cases}$
   (2) $G(n) = 3n + 1$, $n \in \{1, 2, 3\}$.

8. 如图，矩形的面积为 10. 如果矩形的长为 $x$，宽为 $y$，对角线为 $d$，周长为 $l$，那么你能获得关于这些量的哪些函数？第8题

9. 一个圆柱形容器的底部直径是 $d$ cm，高是 $h$ cm，现在以 $v$ cm³/s 的速度向容器内注入某种溶液，求容器内溶液的高度 $x$ cm 与注入溶液的时间 $t$ s 之间的函数解析式，并写出函数的定义域和值域.

42

第一章 集合与函数概念

第一章

10. 在学校的洗衣店中每洗一次衣服(4.5公斤以内)需要付费4元，如果在这家店洗衣10次以后可以免费洗一次。

(1) 根据题意填写下表：

洗衣次数 n	5	9	10	11	15
洗衣费用 c

(2) “费用 c 是次数 n 的函数”还是“次数 n 是费用 c 的函数”？

(3) 写出函数的解析式，并画出图象。

11. 函数 $f(x) = [x]$ 的函数值表示不超过 $x$ 的最大整数，例如，$[-3.5] = -4$，$[2.1] = 2$。当 $x \in (-2.5, 3]$ 时，写出函数 $f(x)$ 的解析式，并作出函数的图像。

12. 某地的出租车按如下方法收费：起步价10元，可行3km（不含3km）；3～7km（不含7km）按1.6元/km计价（不足1km按1km计算）；7km之后都按2.4元/km计价（不足1km按1km计算），试写出以行驶里程（单位：km）为自变量，车费（单位：元）为函数值的函数解析式，并画出这个函数的图像。

13. 21世纪游乐园要建造一个直径为20m的圆形喷水池，如图所示。计划在喷水池的周边靠近水面的位置安装一圈喷水头，使喷出的水柱在离池中心4m处达到最高，高度为6m。另外还要在喷水池的中心设计一个装饰物，使各方向喷来的水柱在此汇合，这个装饰物的的高度应当如何设计？

喷水池

14. 设集合 $A = \{a, b, c\}$，$B = \{0, 1\}$，试问：从A到B的映射共有几个？并将它们分别表示出来。

B组

1. 求下列函数的定义域：

(1) $f(x) = \frac{6}{|1 - |x||} $

(2) $f(x) = \frac{\sqrt{x+4}}{x+2}$

43

CHAPTER

普通高中课程标准实验教科书 数学 1

(3) $f(x) = \sqrt{x-3}$ ;

(4) $f(x) = \frac{1}{\sqrt{3x-1}}$

2. 函数 $r = f(p)$ 的图象如右图所示，

(1) 函数 $r = f(p)$ 的定义域可能是什么？

(2) 函数 $r = f(p)$ 的值域可能是什么？

(3) $r$ 的哪些值只与 $p$ 的一个值对应？

图

3. 画出定义域为 $\{x|-3 \le x \le 8, x \ne 5\}$，值域为 $\{y|-1 \le y \le 2, y \ne 0\}$ 的一个函数的图象。

(1) 如果平面直角坐标系中点 $P(x, y)$ 的坐标满足 $-3 \le x \le 8$，$-1 \le y \le 2$，那么其中哪些点不能在图象上？

(2) 将你的图象和其他同学的相比较，有什么差别吗？

4. 如图所示，一座小岛距离海岸线上最近的 P 点的距离是 2 km，从 P 点沿海岸正东 12 km 处有一个城镇。

图

(1) 假设一个人驾驶的小船的平均速度为 3 km/h，步行的速度是 5 km/h，时间 $t$ (单位：h) 表示他从小岛到城镇的时间，$x$ (单位：km) 表示此人将船停在海岸处距 P 点的距离，请将 $t$ 表示为 $x$ 的函数。

(2) 如果将船停在距 P 点 4 km 处，那么从小岛到城镇要多长时间（精确到 1 h）？

(3) 是否有一个停船的位置使得从小岛到城镇花费的时间最少？你认为这个位置是距离 P 点近还是距离城镇近？为什么？（提示：可以画出函数图象。）

30

44

第一章 集合与函数概念

函数概念的发展历程

17世纪，科学家们致力于运动的研究，如计算天体的位置，远距离航海中对经度和纬度的测量，炮弹的速度对于高度和射程的影响等，诸如此类的问题都需要探究两个变量之间的关系，并根据这种关系对事物的变化规律作出判断，如根据炮弹的速度推测它能达到的高度和射程，这正是函数产生和发展的背景。

“function”一词最初由德国数学家莱布尼兹 (G. W. Leibniz, 1646—1716) 在1692年使用。在中国，清代数学家李善兰 (1811—1882) 在1859年和英国传教士伟烈亚力合译的《代微积拾级》中首次将“function”译做“函数”。

莱布尼兹用“函数”表示随曲线的变化而改变的几何量，如坐标、切线等。1718年，他的学生、瑞士数学家约翰·伯努利 (J. Bernoulli, 1667—1748)强调函数要用公式表示。后来，数学家认为这不是判断函数的标准，只要一些变量变化，另一些变量随之变化就可以了。所以，1755年，瑞士数学家欧拉 (L. Euler, 1707—1783) 将函数定义为“如果某些变量，以一种方式依赖于另一些变量，我们将前面的变量称为后面变量的函数”。

当时很多数学家对于不用公式表示函数很不习惯，甚至抱怀疑态度，函数的概念仍然是比较模糊的。

随着对微积分研究的深入，18世纪末19世纪初，人们对函数的认识向前推进了。德国数学家狄利克雷 (P. G. L. Dirichlet, 1805—1859) 在1837年时提出：“如果对于x的每一个值，y总有一个完全确定的值与之对应，则y是x的函数”，这个定义较清楚地说明了函数的内涵，只要有一个法则，使得取值范围中的每一个值，有一个确定的y和它对应就行了，不管这个法则是公式、图象、表格还是其他形式。19世纪70年代以后，随着集合概念的出现，函数概念又进而用更加严谨的集合和对应语言表述，这就是本节学习的函数概念。

综上所述可知，函数概念的发展与生产、生活以及科学技术的实际需要紧密相关，而且随着研究的深入，函数概念不断得到严谨化、精确化的表达，这与我们学习函数的过程是一样的。

你能以函数概念的发展为背景，谈谈从初中到高中学习函数概念的体会吗？

31

44