1.3 函数的基本性质
1.3 函数的基本性质
45
CHAPTER 1.3 函数的基本性质
在事物变化过程中,保持不变的特征就是这个事物的性质。
函数是描述事物运动变化规律的数学模型。如果了解了函数的变化规律,那么也就基本把握了相应事物的变化规律,因此研究函数的性质,如函数在什么时候递增或递减,有没有最大值或最小值,函数图象有什么特征等,是非常重要的。
观察图 1.3-1 中的各个函数图象,你能说说它们分别反映了相应函数的哪些变化规律吗?
1.3.1 单调性与最大(小)值
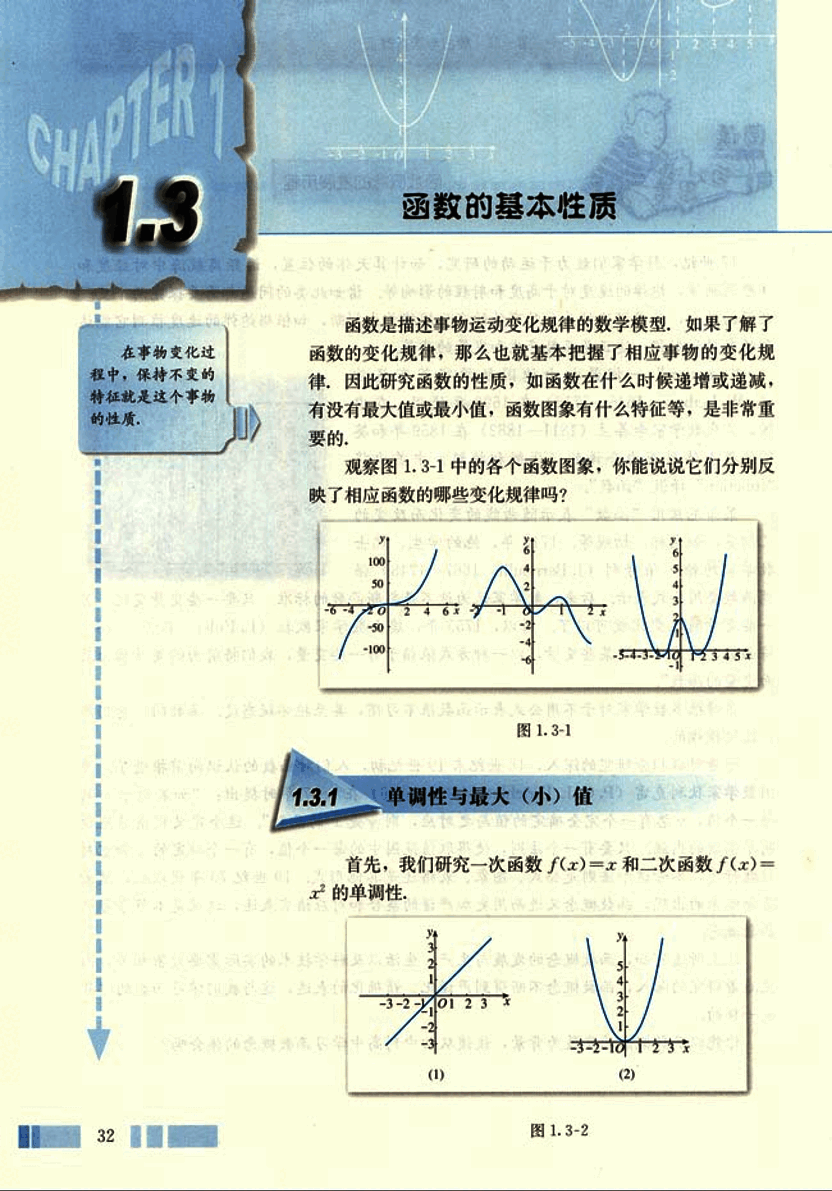
首先,我们研究一次函数 和二次函数 的单调性。
46
第一章 集合与函数概念
观察图象与函数的单调性
观察图 1.3-2,可以看到:
函数 的图象由左至右是上升的;函数 的图象在 y 轴左侧是下降的,在 y 轴右侧是上升的。函数图象的“上升”“下降”反映了函数的一个基本性质——单调性。那么,如何描述函数图象的“上升”“下降”呢?
以二次函数 为例,列出 x, y 的对应值表 1-3。
表 1-3
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|
| … | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | … |
对比图 1.3-2(2) 和表 1-3,可以发现:
图象在 y 轴左侧“下降”,也就是,在区间 上,随着 x 的增大,相应的 反而随着减小;图象在 y 轴右侧“上升”,也就是,在区间 上,随着 x 的增大,相应的 也随着增大。
如何描述函数的单调性
如何利用函数解析式 描述“随着 x 的增大,相应的 随着减小。”“随着 x 的增大,相应的 也随着增大。”?
函数的增减性
对于二次函数 ,我们可以这样来描述“在区间 上,随着 x 的增大,相应的 也随着增大。”: 在区间 上,任取两个 ,得到 ,当 时,有 ,这时,我们就说函数 在区间 上是增函数。
一般地,设函数 的定义域为 I:
如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 ,当 时,都有 ,那么就说函数 在区间 D 上是增函数 (increasing function) (图 1.3-3(1));
如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 ,当 时,都有 ,那么就说函数 在区间 D 上是减函数 (decreasing function) (图 1.3-3(2))。
33

47
CHAPTER 1
普通高中课程标准实验教科书 数学 1
图1.3-3
如果函数 在区间D上是增函数或减函数,那么就说函数 在这一区间具有(严格的)单调性,区间D叫做 的单调区间。
例1
图 1.3-4 是定义在区间 上的函数 ,根据图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?
解:函数 的单调区间有 ,,,。其中 在区间 , 上是减函数,在区间 , 上是增函数。
例2
物理学中的玻意耳定律 (k为正常数)告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大,试用函数的单调性证明之。
分析:按题意,只要证明函数 在区间 上是减函数即可。
证明:根据单调性的定义,设 , 是定义域
48
第一章 集合与函数概念
第一章
(0,+∞)上的任意两个实数,且V₁<V₂,则
由V₁,V₂∈(0,+∞),得V₁V₂>0;
由V₁<V₂,得V₂-V₁>0.
又k>0,于是
即
所以,函数,V∈(0,+∞)是减函数,也就是
说,当体积V减小时,压强p将增大.
探究
画出反比例函数的图象。
(1)这个函数的定义域I是什么?
(2)它在定义域I上的单调性是怎样的?证明你的结论。
思考
我们再来观察本节的图1.3-2,比较其中的两个函数图
象,可以发现,函数的图象上有一个最低点
(0,0),即对于任意的x∈R,都有,当一个函
数f(x)的图象有最低点时,我们就说函数f(x)有最小值.
而函数f(x)=x的图象没有最低点,所以函数f(x)=x没有
最小值.
你能以函数f(x)=x²为例说明函数f(x)的最大值的含义吗?
35

49
CHAPTER
普通高中课程标准实验教科书 数学 1
一般地,设函数 的定义域为 ,如果存在实数 满足:
(1) 对于任意的 ,都有 ;
(2) 存在 ,使得 。
那么,我们称 是函数 的最大值 (maximum value).
你能仿照函数最大值的定义,给出函数 的最小值 (minimum value) 的定义吗?
例 3 “菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点(大约是在距地面高度 25 m 到 30 m 处)时爆裂。如果在距地面高度 18 m 的地方点火,并且烟花冲出的速度是 14.7 m/s.
(1) 写出烟花距地面的高度与时间之间的关系式;
(2) 烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到 1 m)?
解:(1) 设烟花在 s 时距地面的高度为 m,则由物体运动原理可知:
(2) 作出函数 的图象(图 1.3-5)。显然,函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度。
36

50
第一章 集合与函数概念
第一章
由二次函数的知识,对于函数$h(t)=-4.9t^2+14.7t+$18,我们有:
当时,函数有最大值
.
于是,烟花冲出后1.5 s是它爆裂的最佳时刻,这时距地面的高度约为29 m.
例4
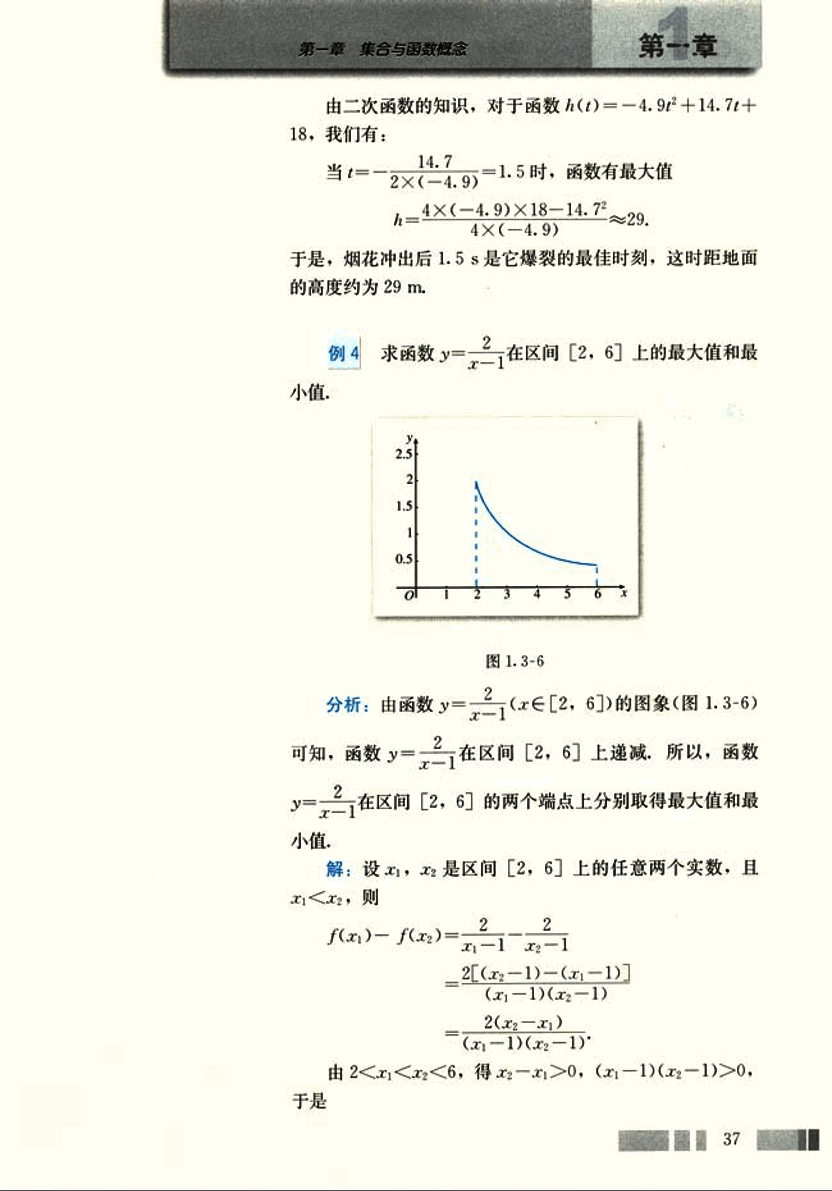
求函数在区间[2, 6]上的最大值和最小值.
分析: 由函数的图象(图1.3-6)
可知,函数在区间[2, 6]上递减,所以,函数在区间[2, 6]的两个端点上分别取得最大值和最小值.
解: 设是区间[2, 6]上的任意两个实数,且,则
由,得,.
于是
37
51
第一章
练习
- 请根据下图描述某装配线的生产效率与生产线上工人数量间的关系。
整个上午 (8:00~12:00) 天气越来越暖,中午时分 (12:00~13:00) 一场暴风雨使天气骤然凉爽了许多,暴风雨过后,天气转暖,直到太阳落山 (18:00) 才又开始转凉。画出这一天 8:00~20:00 期间气温作为时间函数的一个可能的图象,并说出所画函数的单调区间。
证明函数 在 R 上是减函数。
设 是定义在区间 上的函数,如果 在区间 上递减,在区间 上递增,画出 的一个大致的图象,从图象上可以发现 是函数 的一个______。
52
1.3.2 奇偶性
观察图1.3-7,思考并讨论以下问题:
(1) 这两个函数图象有什么共同特征吗?
(2) 相应的两个函数值对应表是如何体现这些特征的?
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|
| 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|
| $f(x) = | x | $ | 3 | 2 | 1 | 0 | 1 |
我们看到,这两个函数的图象都关于y轴对称,那么,如何利用函数解析式描述函数图象的这个特征呢?
从函数值对应表可以看到,当自变量x取一对相反数时,相应的两个函数值相同。
例如,对于函数有:
实际上,对于R内任意的一个x,都有,这时我们称函数为偶函数。
一般地,如果对于函数的定义域内任意一个x,
53
CHAPTER
普通高中课程标准实验教科书 数学 1
都有 ,那么函数 就叫做偶函数 (even function).
例如,偶函数 , 都是偶函数,它们的图象分别如图 1.3-8(1)(2) 所示。
观察函数 和 的图象 (图 1.3-9),并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|
| / |
我们看到,两个函数的图象都关于原点对称,函数图象的这个特征,反映在函数解析式上就是:
当自变量 x 取一对相反数时,相应的函数值 也是
40
54
第一章 集合与函数概念
一对相反数
例如,对于函数 有:
;
;
.
实际上,对于函数 定义域内任意一个 ,都有 ,这时我们称函数 为奇函数。
一般地,如果对于函数 的定义域内任意一个 ,都有 ,那么函数 就叫做奇函数 (odd function)。
思考
(1) 判断函数 的奇偶性。
(2) 如果图 1.3-10 是函数 图象的一部分,你能根据 的奇偶性画出它在 y 轴左边的图象吗?
例 5
判断下列函数的奇偶性:
(1) ;
(2) ;
(3) ;
(4) ;
41

55
CHAPTER
普通高中课程标准实验教科书 数学 1
解:(1) 对于函数 ,其定义域为 。
因为对定义域内的每一个 ,都有
,
所以,函数 为偶函数。
(2) 对于函数 ,其定义域为 。
因为对定义域内的每一个 ,都有
,
所以,函数 为奇函数。
(3) 对于函数 ,其定义域为 。
因为对于定义域内的每一个 ,都有
,
所以,函数 为奇函数。
(4) 对于函数 ,其定义域为 。
因为对于定义域内的每一个 ,都有
,
所以,函数 为偶函数。
练习
- 已知 是偶函数, 是奇函数,试将下图补充完整。
- 判断下列函数的奇偶性:
(1) ;
(2) .
42
56
第一章 集合与函数概念
用计算机绘制函数图象
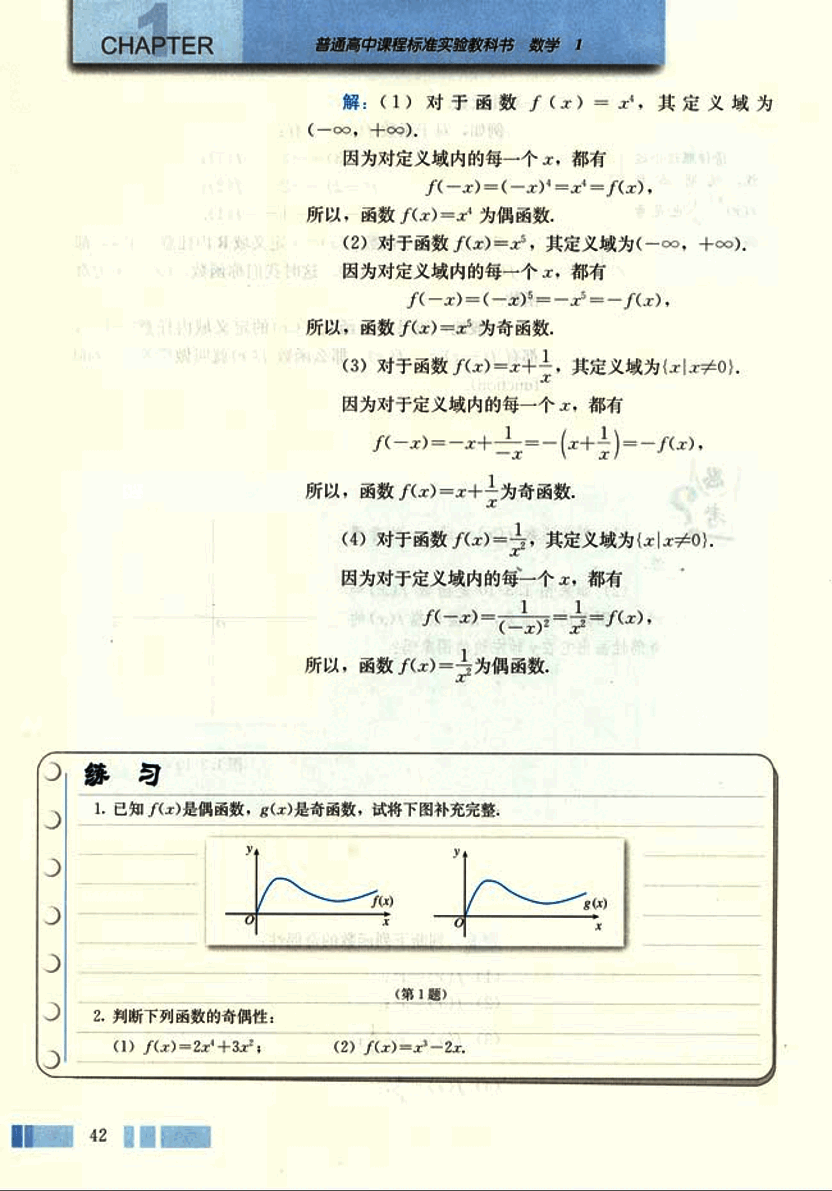
利用计算机软件可以便捷、迅速地绘制各种函数图象。不同的计算机软件绘制函数图象的具体操作不尽相同,但都是基于我们熟悉的描点作图,即给自变量赋值,用计算法则算出相应的函数值,再由这些对应值生成一系列的点,最后连接这些点描绘出函数图象。下面以Excel和《几何画板》为例,介绍用计算机软件作函数图象的方法。
- 用“Excel”绘制函数 的图象
(1) 打开Excel,在A列输入自变量的值;
(2) 把光标移到B列,在编辑框输入计算法则“=POWER(A:A, 3)”回车,在B列生成相应的函数值,如图1所示;
(3) 选中数据区域A、B列,执行“插入→图表”命令,在“图表类型”中选择“XY散点图”,根据需要在“子图表类型”中选择其一,然后按照对话框中的提示,完成制图操作,就可得到如图2所示的函数 的图象。
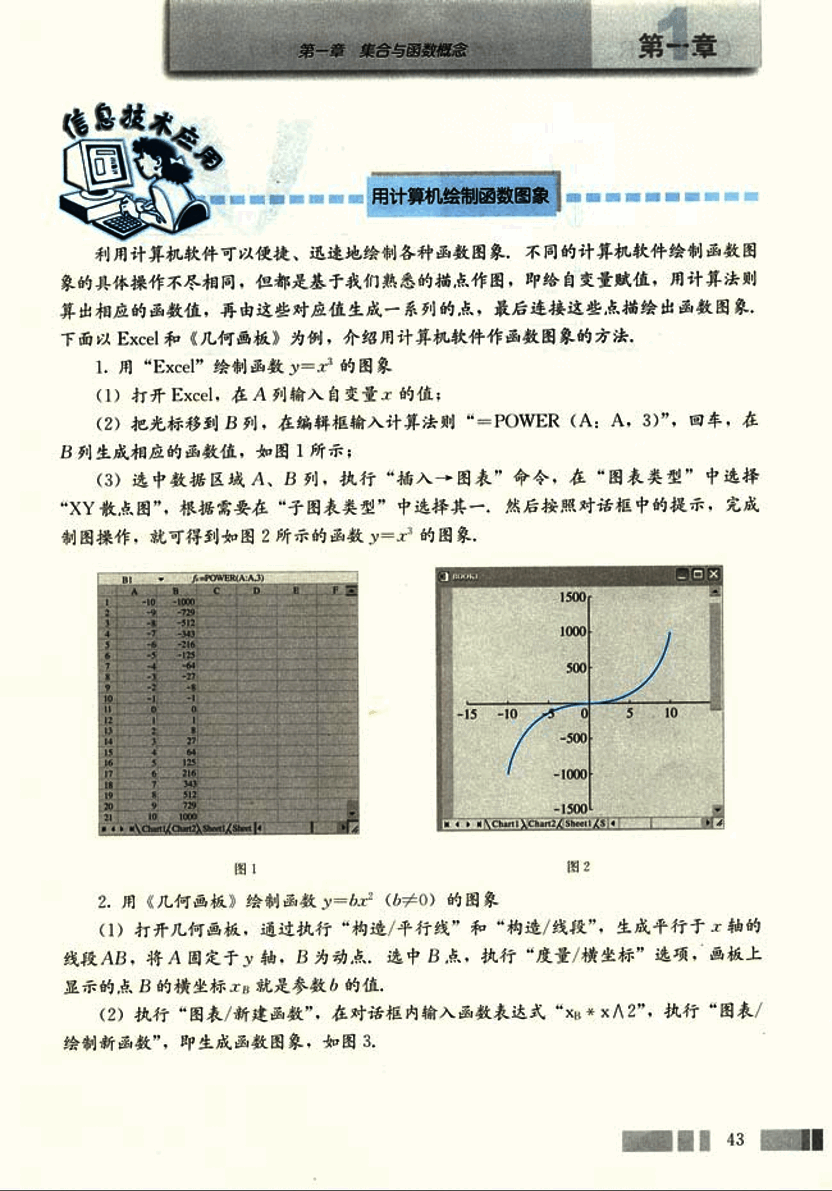
- 用《几何画板》绘制函数 () 的图象
(1) 打开几何画板,通过执行“构造/平行线”和“构造/线段”,生成平行于x轴的线段AB,将A固定于y轴,B为动点。选中B点,执行“度量/横坐标”选项,画板上显示的点B的横坐标 就是参数b的值;
(2) 执行“图表/新建函数”,在对话框内输入函数表达式“”,执行“图表/绘制新函数”,即生成函数图象,如图3。
43
57
CHAPTER
普通高中课程标准实验教科书 数学 1
图3 图4
当你左右移动B点的位置时,函数 就会“动”起来,如图4.如果有条件,请你绘制函数 的图象,并探究系数a、b、c对函数图象的影响。
44
58
第一章 集合与函数概念
习题1.3
A组
x∈R时,一次函数y=mx+b在m<0和m>0时的单调性是怎样的?利用函数单调性的定义证明你的结论。
画出下列函数的图象,并根据图象说出y=f(x)的单调区间,以及在各单调区间上,函数y=f(x)是增函数还是减函数。
(1) y=x²-5x+5;
(2) y=9-x².证明:
(1) 函数f(x)=x²+1在(-∞,0)上是减函数;
(2) 函数f(x)=1-x²在(-∞,0)上是增函数。根据下图说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数。
(第4题)
一名心率过速患者服用某种药物后心率立刻明显减慢,之后随着药力的减退,心率再次慢慢升高,画出自服药那一刻起,心率关于时间的一个可能的图象(示意图)。
一个鹿群在开始观察时有3500头,经过2个月的观察,搜集到了下面的数据,表格中的数据反映出鹿群数量随时间的变化具有一定的规律,请根据表格回答以下问题。
| 天数 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数量 | 3 500 | 3 750 | 4 250 | 4 500 | 4 250 | 3 750 | 3 500 | 3 750 | 4 250 | 4 500 | 4 250 | 3 750 | 3 500 |
(1) 鹿群数量何时增加?何时减少?
(2) 鹿群在第一个月哪一天数量最多?哪一天数量最少?
45
59
CHAPTER
普通高中课程标准实验教科书 数学 1
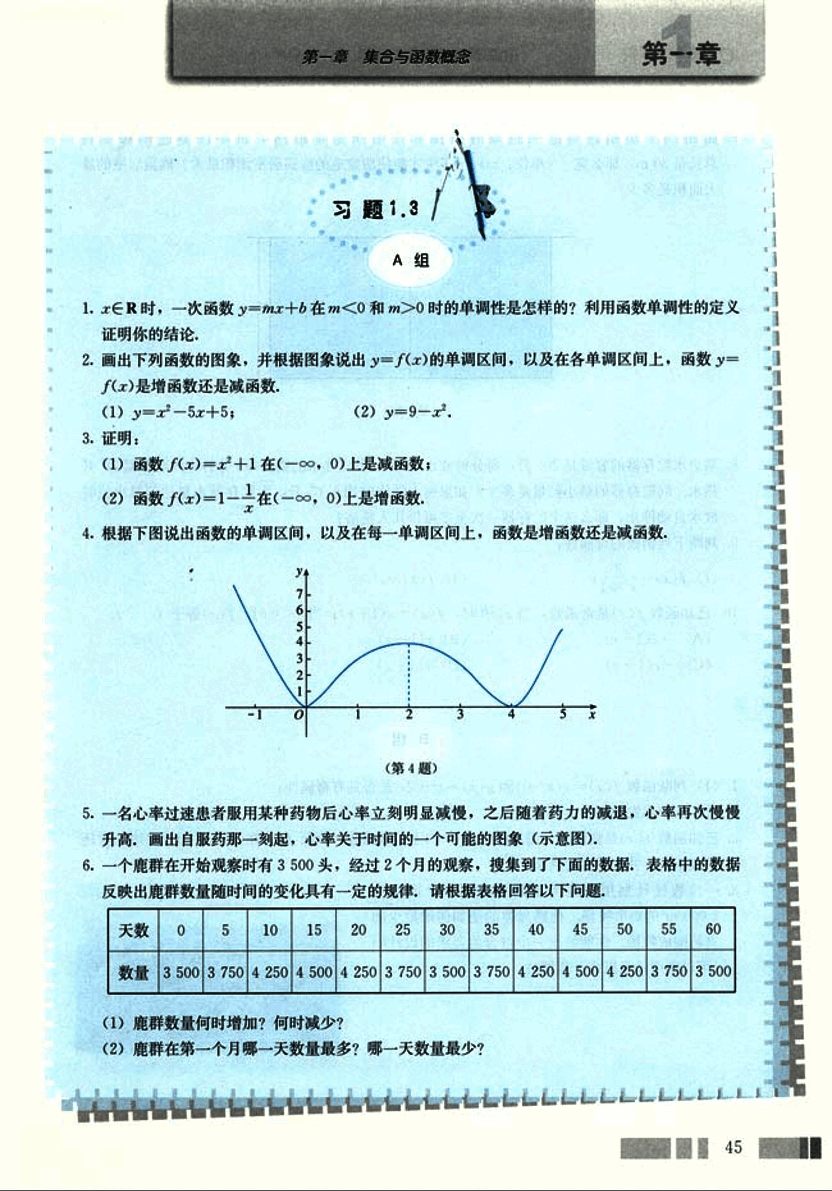
7.如图所示,动物园要建造一面靠墙的2间面积相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m,那么宽x(单位:m)为多少才能使所建造的熊猫居室面积最大?熊猫居室的最大面积是多少?
8.1
(第7题)
8.某热水贮存器的容量是200升,每分钟放水34升,供应热水的锅炉每分钟注入贮存器2升热水,问贮存器的最小贮量是多少?如果每人洗浴时用水65升,而贮存器水量达到最小值时放水自动停止,那么这个贮存器一次至多可供几人洗浴?
9.判断下列函数的奇偶性:
(1)
(2) .
10.已知函数f(x)是奇函数,当x>0时,;当x<0时,f(x)等于( )。
(A)
(B)
(C)
(D)
B组
1.(1)判断函数和是否具有奇偶性;
(2)从中你发现了什么?
2.已知函数f(x)是偶函数,而且在(0,+∞)上是减函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的判断。
3.一位牧民计划用篱笆为他的马群围一个面积为2000 m²的矩形牧场,他感兴趣的是如何用最少的篱笆围成牧场,你能给出一个符合他要求的设计吗(可以利用计算机或计算器)?
46
