69
先让我们一起来看两个问题.
据国务院发展研究中心2000年发表的《未来20年我国发展前景分析》判断,未来20年,我国GDP(国内生产总值)年平均增长率可望达到7.3%.那么,在2001~2020年,各年的GDP可望为2000年的多少倍?
如果把我国2000年GDP看成是1个单位,2001年为第1年,那么:
1年后(即2001年),我国的GDP可望为2000年的(1+7.3%)倍;
2年后(即2002年),我国的GDP可望为2000年的(1+7.3%)²倍;
3年后(即2003年),我国的GDP可望为2000年的___倍;
4年后(即2004年),我国的GDP可望为2000年的___倍;
……
设x年后我国的GDP为2000年的y倍,那么x =1.073x (x∈N, x<20).
即从2000年起,x年后我国的GDP为2000年的1.073x 倍.
想一想,正整数指数幂1.073x 的含义是什么,它具有哪些运算性质,
当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”,根据此规律,人们获得了生物体内碳14含量P与死亡年数t之间的关系
P = ( 1 2 ) t 5730 P = (\frac{1}{2})^{\frac{t}{5730}} P = ( 2 1 ) 5730 t
按照惯例,人们将生物体死亡时,每克组织的碳14含量作为1个单位.
考古学家根据 (*) 式可以知道,生物死亡 t 年后,体内碳 14 含量 P 的值。例如,
当生物死亡了 5730,2 × 5730,3 × 5730,…… 年后,它体内碳 14 的含量 P 分别为 ( 1 2 ) (\frac{1}{2}) ( 2 1 ) ( 1 2 ) 2 (\frac{1}{2})^2 ( 2 1 ) 2 ( 1 2 ) 3 (\frac{1}{2})^3 ( 2 1 ) 3
当生物体死亡了 6000 年,10000 年,100000 年后,根据 (*) 式,它体内碳 14 的含量 P 分别为 ( 1 2 ) 6000 5730 (\frac{1}{2})^{\frac{6000}{5730}} ( 2 1 ) 5730 6000 ( 1 2 ) 10000 5730 (\frac{1}{2})^{\frac{10000}{5730}} ( 2 1 ) 5730 10000 ( 1 2 ) 100000 5730 (\frac{1}{2})^{\frac{100000}{5730}} ( 2 1 ) 5730 100000
在问题 2 中,我们已经知道 ( 1 2 ) (\frac{1}{2}) ( 2 1 ) ( 1 2 ) 2 (\frac{1}{2})^2 ( 2 1 ) 2 ( 1 2 ) 3 (\frac{1}{2})^3 ( 2 1 ) 3 1 2 \frac{1}{2} 2 1 1 4 \frac{1}{4} 4 1 1 8 \frac{1}{8} 8 1 ( 1 2 ) 10000 5730 (\frac{1}{2})^{\frac{10000}{5730}} ( 2 1 ) 5730 10000 ( 1 2 ) 6000 5730 (\frac{1}{2})^{\frac{6000}{5730}} ( 2 1 ) 5730 6000 ( 1 2 ) 100000 5730 (\frac{1}{2})^{\frac{100000}{5730}} ( 2 1 ) 5730 100000
下面,我们一起将指数的取值范围从整数推广到实数。为此,需要先学习根式的知识。
我们知道,如果 x 2 = a x^2 = a x 2 = a x 叫做 a 的平方根,例如,±2 就是 4 的平方根;如果 x 3 = a x^3 = a x 3 = a x 叫做 a 的立方根,例如,2 就是 8 的立方根。
类似地,由于 (±2)4 ^4 4 5 ^5 5
一般地,如果 x n = a x^n = a x n = a x 叫做 a 的 n 次方根 (n th root),其中 n > 1,且 n ∈ N ∗ n∈N^* n ∈ N ∗
当 n 是奇数时,正数的 n 次方根是一个正数,负数的 n 次方根是一个负数,这时,a 的 n 次方根用符号 a n \sqrt[n]{a} n a
32 5 = 2 \sqrt[5]{32} = 2 5 32 = 2 − 32 5 = − 2 \sqrt[5]{-32} = -2 5 − 32 = − 2 a 3 3 = a 2 \sqrt[3]{a^3} = a^2 3 a 3 = a 2
57
普通高中课程标准实验教科书 数学 1
当 n 为偶数时,正数的 n 次方根有两个,这两个数互为相反数。这时,正数的正的 n 次方根用符号 a n \sqrt[n]{a} n a n 次方根用符号 − a n -\sqrt[n]{a} − n a n 次方根与负的 n 次方根可以合并写成 ±a n \sqrt[n]{a} n a a > 0)。例如
16 4 = 2 \sqrt[4]{16} = 2 4 16 = 2 − 16 4 = − 2 -\sqrt[4]{16} = -2 − 4 16 = − 2
16 的 4 次方根可以表示为 ±16 4 = ± 2 \sqrt[4]{16} = ±2 4 16 = ± 2
负数没有偶次方根。
0 的任何次方根都是 0,记作 0 n = 0 \sqrt[n]{0} = 0 n 0 = 0
式子 a n \sqrt[n]{a} n a n 叫做根指数 (radical exponent),a 叫做被开方数 (radicand)。
根据 n 次方根的意义,可得
( a n ) n = a (\sqrt[n]{a})^n = a ( n a ) n = a
例如,( 5 ) 2 = 5 (\sqrt{5})^2 = 5 ( 5 ) 2 = 5 ( − 3 5 ) 5 = − 3 (\sqrt[5]{-3})^5 = -3 ( 5 − 3 ) 5 = − 3
a n \sqrt[n]{a} n a a 的 n 次方根,等式 a n n = a \sqrt[n]{a^n} = a n a n = a a n n \sqrt[n]{a^n} n a n
通过探究可以得到:
当 n 为奇数时,a n n = a \sqrt[n]{a^n} = a n a n = a
当 n 为偶数时,a n n = ∣ a ∣ = { a , a ≥ 0 − a , a < 0 \sqrt[n]{a^n} = |a| = \begin{cases} a, & a \ge 0 \\ -a, & a < 0 \end{cases} n a n = ∣ a ∣ = { a , − a , a ≥ 0 a < 0
例 1 求下列各式的值:
(1) ( − 8 ) 3 3 \sqrt[3]{(-8)^3} 3 ( − 8 ) 3 ( − 10 ) 2 \sqrt{(-10)^2} ( − 10 ) 2
(3) ( 3 − π ) 2 \sqrt{(3 - \pi)^2} ( 3 − π ) 2 ( a − b ) 2 \sqrt{(a - b)^2} ( a − b ) 2 a > b )。
解: (1) ( − 8 ) 3 3 = − 8 \sqrt[3]{(-8)^3} = -8 3 ( − 8 ) 3 = − 8
(2) ( − 10 ) 2 = ∣ − 10 ∣ = 10 \sqrt{(-10)^2} = |-10| = 10 ( − 10 ) 2 = ∣ − 10∣ = 10
(3) ( 3 − π ) 2 = ∣ 3 − π ∣ = π − 3 \sqrt{(3 - \pi)^2} = |3 - \pi| = \pi - 3 ( 3 − π ) 2 = ∣3 − π ∣ = π − 3
(4) ( a − b ) 2 = ∣ a − b ∣ = a − b \sqrt{(a - b)^2} = |a - b| = a - b ( a − b ) 2 = ∣ a − b ∣ = a − b a > b )。
58
我们来看下面的例子,根据 n n n
a 10 5 = ( a 2 ) 5 5 = a 2 = a 10 5 \sqrt[5]{a^{10}} = \sqrt[5]{(a^2)^5} = a^2 = a^{\frac{10}{5}} 5 a 10 = 5 ( a 2 ) 5 = a 2 = a 5 10 a > 0 a>0 a > 0
a 12 3 = ( a 4 ) 3 3 = a 4 = a 12 3 \sqrt[3]{a^{12}} = \sqrt[3]{(a^4)^3} = a^4 = a^{\frac{12}{3}} 3 a 12 = 3 ( a 4 ) 3 = a 4 = a 3 12 a > 0 a>0 a > 0
这就是说,当根式的被开方数的指数能被根指数整除时,根式可以表示为分数指数幂的形式。
那么,当根式的被开方数的指数不能被根指数整除时,根式是否也可以表示为分数指数幂的形式呢?例如,能否把 a 3 \sqrt[3]{a} 3 a b \sqrt{b} b c 5 \sqrt[5]{c} 5 c
a 3 = a 1 3 \sqrt[3]{a} = a^{\frac{1}{3}} 3 a = a 3 1 a > 0 a>0 a > 0
b = b 1 2 \sqrt{b} = b^{\frac{1}{2}} b = b 2 1 b > 0 b>0 b > 0
c 5 = c 1 5 \sqrt[5]{c} = c^{\frac{1}{5}} 5 c = c 5 1 c > 0 c>0 c > 0
如果可以,那么整数指数幂的运算性质 ( a m ) n = a m n (a^m)^n = a^{mn} ( a m ) n = a mn
我们规定正数的正分数指数幂的意义是
a m n = a m n a^{\frac{m}{n}} = \sqrt[n]{a^m} a n m = n a m a > 0 a>0 a > 0 m m m n ∈ N n \in N n ∈ N n > 1 n>1 n > 1
于是,在条件 a > 0 a>0 a > 0 m m m n ∈ N n \in N n ∈ N n > 1 n>1 n > 1
正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定
a − m n = 1 a m n a^{-\frac{m}{n}} = \frac{1}{a^{\frac{m}{n}}} a − n m = a n m 1 a > 0 a>0 a > 0 m m m n ∈ N n \in N n ∈ N n > 1 n>1 n > 1
例如,5 − 1 2 = 1 5 1 2 = 1 5 5^{-\frac{1}{2}} = \frac{1}{5^{\frac{1}{2}}} = \frac{1}{\sqrt{5}} 5 − 2 1 = 5 2 1 1 = 5 1 a − 1 3 = 1 a 1 3 = 1 a 3 a^{-\frac{1}{3}} = \frac{1}{a^{\frac{1}{3}}} = \frac{1}{\sqrt[3]{a}} a − 3 1 = a 3 1 1 = 3 a 1 a > 0 a>0 a > 0
0 的正分数指数幂等于 0,0 的负分数指数幂没有意义。
规定了分数指数幂的意义以后,指数的概念就从整数指数推广到了有理数指数。
整数指数幂的运算性质对于有理指数幂也同样适用,即对于任意有理数 r r r s s s
(1) a r a s = a r + s a^r a^s = a^{r+s} a r a s = a r + s a > 0 a>0 a > 0 r r r s ∈ Q s \in Q s ∈ Q
(2) ( a r ) s = a r s (a^r)^s = a^{rs} ( a r ) s = a rs a > 0 a>0 a > 0 r r r s ∈ Q s \in Q s ∈ Q
(3) ( a b ) r = a r b r (ab)^r = a^r b^r ( ab ) r = a r b r a > 0 a>0 a > 0 b > 0 b>0 b > 0 r ∈ Q r \in Q r ∈ Q
59
普通高中课程标准实验教科书 数学 1
对于本节开头的问题2,考古学家正是利用有理数指数幂的知识,计算出生物死亡6000年,10000年,100000年后体内碳14含量P的值,例如
当t=6000时,P = ( 1 2 ) 5730 5730 ≈ 0.484 P = (\frac{1}{2})^{\frac{5730}{5730}} \approx 0.484 P = ( 2 1 ) 5730 5730 ≈ 0.484
8 3 2 8^{\frac{3}{2}} 8 2 3 25 − 1 2 25^{-\frac{1}{2}} 2 5 − 2 1 ( 1 2 ) − 5 (\frac{1}{2})^{-5} ( 2 1 ) − 5 ( 16 81 ) − 1 2 (\frac{16}{81})^{-\frac{1}{2}} ( 81 16 ) − 2 1
解:8 3 2 = ( 2 3 ) 3 2 = 2 9 2 = 2 4 = 4 8^{\frac{3}{2}} = (2^3)^{\frac{3}{2}} = 2^{\frac{9}{2}} = 2^4 = 4 8 2 3 = ( 2 3 ) 2 3 = 2 2 9 = 2 4 = 4
25 − 1 2 = ( 5 2 ) − 1 2 = 5 − 1 = 1 5 25^{-\frac{1}{2}} = (5^2)^{-\frac{1}{2}} = 5^{-1} = \frac{1}{5} 2 5 − 2 1 = ( 5 2 ) − 2 1 = 5 − 1 = 5 1
( 1 2 ) − 5 = ( 2 − 1 ) − 5 = 2 5 = 32 (\frac{1}{2})^{-5} = (2^{-1})^{-5} = 2^5 = 32 ( 2 1 ) − 5 = ( 2 − 1 ) − 5 = 2 5 = 32
( 16 81 ) − 1 2 = ( 2 3 ) − 1 = 3 2 = 27 8 (\frac{16}{81})^{-\frac{1}{2}} = (\frac{2}{3})^{-1} = \frac{3}{2} = \frac{27}{8} ( 81 16 ) − 2 1 = ( 3 2 ) − 1 = 2 3 = 8 27
a 3 ⋅ a a^3 \cdot \sqrt{a} a 3 ⋅ a a 2 ⋅ a 2 3 a^2 \cdot \sqrt[3]{a^2} a 2 ⋅ 3 a 2 a 3 \sqrt[3]{\sqrt{a}} 3 a
解:a 3 ⋅ a = a 3 ⋅ a 1 2 = a 3 + 1 2 = a 7 2 a^3 \cdot \sqrt{a} = a^3 \cdot a^{\frac{1}{2}} = a^{3+\frac{1}{2}} = a^{\frac{7}{2}} a 3 ⋅ a = a 3 ⋅ a 2 1 = a 3 + 2 1 = a 2 7
a 2 ⋅ a 2 3 = a 2 ⋅ a 2 3 = a 2 + 2 3 = a 8 3 a^2 \cdot \sqrt[3]{a^2} = a^2 \cdot a^{\frac{2}{3}} = a^{2+\frac{2}{3}} = a^{\frac{8}{3}} a 2 ⋅ 3 a 2 = a 2 ⋅ a 3 2 = a 2 + 3 2 = a 3 8
a 3 = ( a 1 2 ) 1 3 = a 1 6 \sqrt[3]{\sqrt{a}} = (a^{\frac{1}{2}})^{\frac{1}{3}} = a^{\frac{1}{6}} 3 a = ( a 2 1 ) 3 1 = a 6 1
(1) ( 2 a b 2 ) ( − 6 a 2 b ) ÷ ( − 3 a 3 b 2 ) (2ab^2)(-6a^2b) \div (-3a^3b^2) ( 2 a b 2 ) ( − 6 a 2 b ) ÷ ( − 3 a 3 b 2 )
(2) ( m 4 n ) 8 (m^4n)^8 ( m 4 n ) 8
解:(1) ( 2 a b 2 ) ( − 6 a 2 b ) ÷ ( − 3 a 3 b 2 ) (2ab^2)(-6a^2b) \div (-3a^3b^2) ( 2 a b 2 ) ( − 6 a 2 b ) ÷ ( − 3 a 3 b 2 )
= [ 2 × ( − 6 ) ÷ ( − 3 ) ] a 1 + 2 − 3 b 2 + 1 − 2 = [2 \times (-6) \div (-3)]a^{1+2-3}b^{2+1-2} = [ 2 × ( − 6 ) ÷ ( − 3 )] a 1 + 2 − 3 b 2 + 1 − 2
= 4 a b = 4ab = 4 ab
= 4 a = 4a = 4 a
= ( m 1 4 ) 8 ( n 1 8 ) 8 = (m^{\frac{1}{4}})^8(n^{\frac{1}{8}})^8 = ( m 4 1 ) 8 ( n 8 1 ) 8
= m 2 n − 3 = m^2n^{-3} = m 2 n − 3
= m 2 n 3 = \frac{m^2}{n^3} = n 3 m 2
(1) 25 3 − 125 3 ÷ 25 3 \sqrt[3]{25} - \sqrt[3]{125} \div \sqrt[3]{25} 3 25 − 3 125 ÷ 3 25
(2) a 2 a ⋅ a 2 3 ( a > 0 ) \frac{a^2}{\sqrt{a} \cdot \sqrt[3]{a^2}} (a > 0) a ⋅ 3 a 2 a 2 ( a > 0 )
(1) 25 3 − 125 3 ÷ 25 3 \sqrt[3]{25} - \sqrt[3]{125} \div \sqrt[3]{25} 3 25 − 3 125 ÷ 3 25
= ( 5 1 3 − 5 3 3 ) ÷ 5 1 3 = (5^{\frac{1}{3}} - 5^{\frac{3}{3}}) \div 5^{\frac{1}{3}} = ( 5 3 1 − 5 3 3 ) ÷ 5 3 1
= 5 1 3 − 5 2 3 − 5 1 3 + 5 1 3 = 5^{\frac{1}{3}} - 5^{\frac{2}{3}} - 5^{\frac{1}{3}} + 5^{\frac{1}{3}} = 5 3 1 − 5 3 2 − 5 3 1 + 5 3 1
= 5 1 3 − 5 1 3 + 5 1 3 = 5^{\frac{1}{3}} - 5^{\frac{1}{3}} + 5^{\frac{1}{3}} = 5 3 1 − 5 3 1 + 5 3 1
= 5 1 3 − 5 = 5^{\frac{1}{3}} - 5 = 5 3 1 − 5
= 5 3 − 5 = \sqrt[3]{5} - 5 = 3 5 − 5
(2) a 2 a ⋅ a 2 3 \frac{a^2}{\sqrt{a} \cdot \sqrt[3]{a^2}} a ⋅ 3 a 2 a 2
= a 2 a 1 2 ⋅ a 2 3 = \frac{a^2}{a^{\frac{1}{2}} \cdot a^{\frac{2}{3}}} = a 2 1 ⋅ a 3 2 a 2
= a 2 − 1 2 − 2 3 = a^{2 - \frac{1}{2} - \frac{2}{3}} = a 2 − 2 1 − 3 2
= a 5 6 = a^{\frac{5}{6}} = a 6 5
= a 5 6 = \sqrt[6]{a^5} = 6 a 5
上面,我们将指数的取值范围由整数推广到了有理数,那么,当指数是无理数时,如 5 5 5^{\sqrt{5}} 5 5
事实上,5 5 5^{\sqrt{5}} 5 5
61
普通高中课程标准实验教科书 数学 1
√2的过剩近似值 55 的近似值 5√2 的近似值 √2的不足近似值 1.5 11.180 339 89 9.518 269 694 1.4 1.42 9.829 635 328 9.672 669 973 1.41 1.415 9.750 851 808 9.735 171 039 1.414 1.414 3 9.739 872 62 9.738 305 174 1.414 2 1.414 22 9.738 618 643 9.738 461 907 1.414 21 1.414 214 9.738 524 602 9.738 508 928 1.414 213 1.414 213 6 9.738 518 332 9.738 516 765 1.414 213 5 1.414 213 57 9.738 517 862 9.738 517 705 1.414 213 56 1.414 213 563 9.738 517 752 9.738 517 736 1.414 213 562 ... ... ... ...
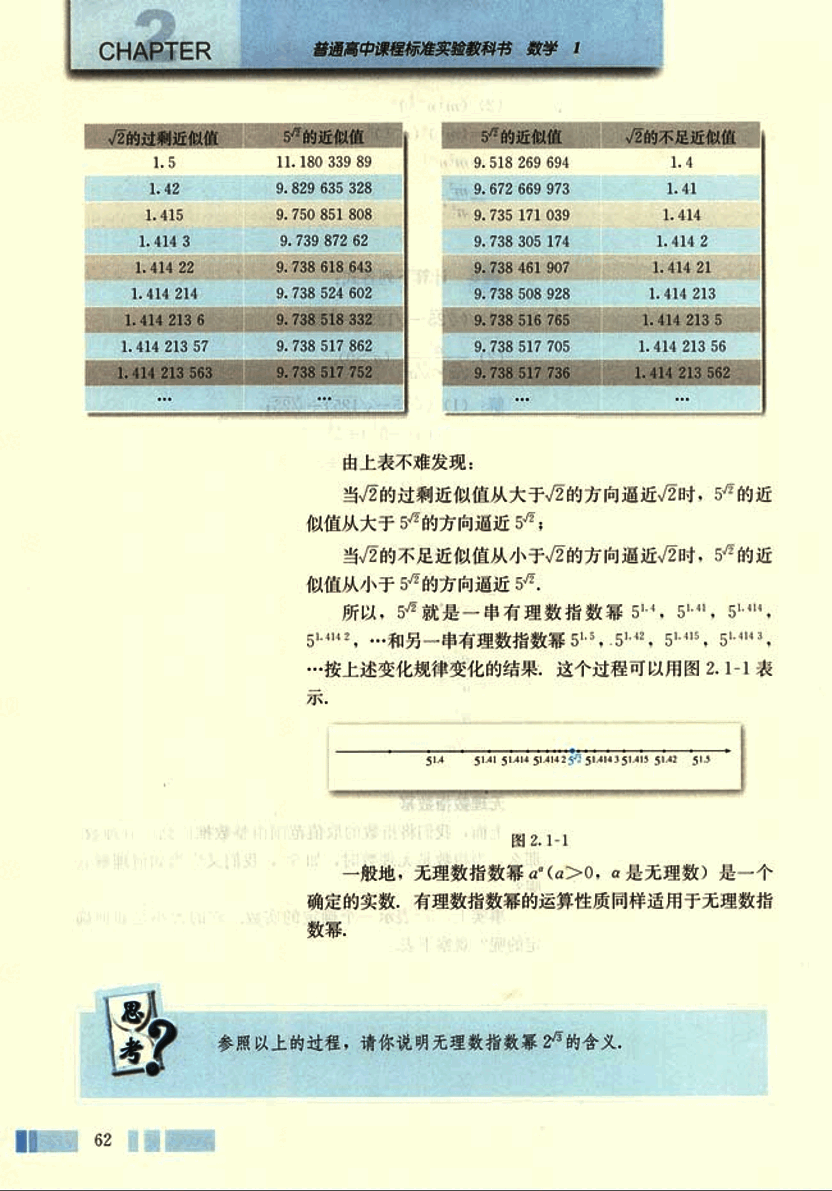
由上表不难发现:
当√2的过剩近似值从大于√2的方向逼近√2时,5√2 的近似值从大于5的方向逼近5;
当√2的不足近似值从小于√2的方向逼近√2时,5√2 的近似值从小于5的方向逼近5√2 .
所以,5√2 就是一串有理数指数幂 51.4 , 51.41 , 51.414 , 51.4142 ,…和另一串有理数指数幂 51.5 , 51.42 , 51.415 , 51.4143 ,…按上述变化规律变化的结果,这个过程可以用图2.1-1表示.
5.14 5.141 5.1414 5.14142 5.14143 5.1415 5.142 5.15
图 2.1-1
一般地,无理数指数幂 a x a^x a x
参照以上的过程,请你说明无理数指数幂2√5 的含义.
62
用根式的形式表示下列各式 (a>0): a 1 2 a^{\frac{1}{2}} a 2 1 a 1 3 a^{\frac{1}{3}} a 3 1 a 1 4 a^{\frac{1}{4}} a 4 1 a 1 n a^{\frac{1}{n}} a n 1
用分数指数幂表示下列各式: (1) x \sqrt{x} x
(2) ( a + b ) 3 \sqrt{(a+b)^3} ( a + b ) 3
(3) ( m − n ) n n \sqrt[n]{(m-n)^n} n ( m − n ) n
(4) ( m − n ) n m \sqrt[m]{(m-n)^n} m ( m − n ) n
(5) p n q n \sqrt[n]{p^n q} n p n q
(6) m 3 m \sqrt{\frac{m^3}{m}} m m 3
计算下列各式: (1) ( 36 49 ) 1 2 (\frac{36}{49})^{\frac{1}{2}} ( 49 36 ) 2 1
(2) 2 3 × 1.5 × 12 2\sqrt{3} \times \sqrt{1.5} \times \sqrt{12} 2 3 × 1.5 × 12
(3) a 1 2 a 1 3 a 1 4 a 1 6 a^{\frac{1}{2}} a^{\frac{1}{3}} a^{\frac{1}{4}} a^{\frac{1}{6}} a 2 1 a 3 1 a 4 1 a 6 1
(4) 2 x 1 2 + ( 1 2 x 1 2 − 2 x − 1 2 ) 2x^{\frac{1}{2}} + (\frac{1}{2}x^{\frac{1}{2}} - 2x^{-\frac{1}{2}}) 2 x 2 1 + ( 2 1 x 2 1 − 2 x − 2 1 )
用计算器求下列各式的值 (精确到 0.000 1): (1) 1.3 1 2 1.3^{\frac{1}{2}} 1. 3 2 1
(2) 0.02 1 3 0.02^{\frac{1}{3}} 0.0 2 3 1
(3) 2 − 0.1 2^{-0.1} 2 − 0.1
(4) ( 2 5 ) 2 3 (\frac{2}{5})^{\frac{2}{3}} ( 5 2 ) 3 2
当底数大于 0 时,我们将指数的取值范围从整数推广到了实数。这样,在本节开头的問題 2 中,对于任意的 t≥0,
P = ( 1 2 ) t 5730 P = (\frac{1}{2})^{\frac{t}{5730}} P = ( 2 1 ) 5730 t
普通高中课程标准实验教科书 数学 1
探究
问题2中的函数P = ( 1 2 ) t 1 / 5 P=( \frac{1}{2} )^{t^{1/5}} P = ( 2 1 ) t 1/5 t ≥ 0 t \ge 0 t ≥ 0 y = 1.073 x y=1.073^x y = 1.07 3 x x ∈ N + , x ≤ 20 x \in N^+, x \le 20 x ∈ N + , x ≤ 20
如果用字母a来代替数( 1 2 ) (\frac{1}{2}) ( 2 1 )
y = a x y = a^x y = a x
的函数,其中自变量x是指数,底数a是一个大于0且不等于1的常量。
一般地,函数y = a x y = a^x y = a x a > 0 a > 0 a > 0 a ≠ 1 a \ne 1 a = 1
下面我们来研究指数函数y = a x y = a^x y = a x a > 0 a > 0 a > 0 a ≠ 1 a \ne 1 a = 1
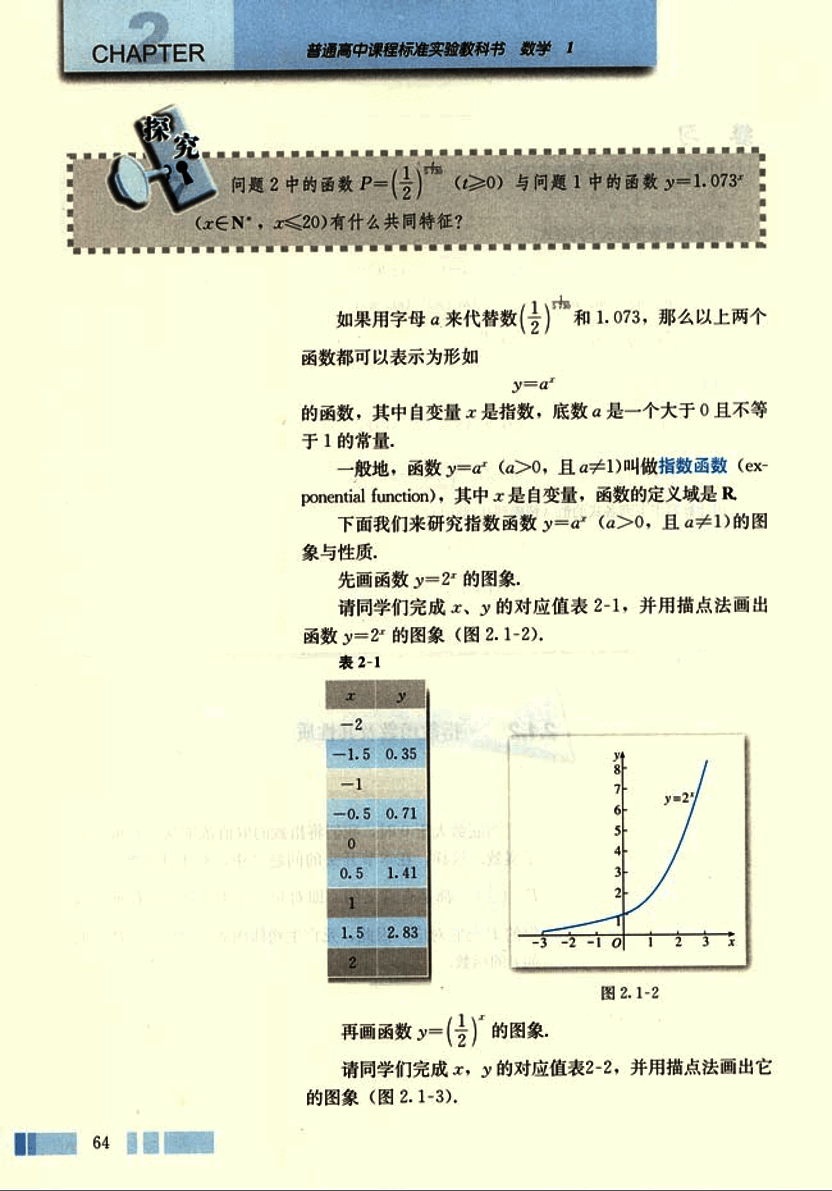
先画函数y = 2 x y = 2^x y = 2 x
请同学们完成x,y的对应值表2-1,并用描点法画出函数y = 2 x y = 2^x y = 2 x
表2-1
x y -2 -1.5 0.35 -1 -0.5 0.71 0 0.5 1.41 1 1.5 2.83 2
图2.1-2
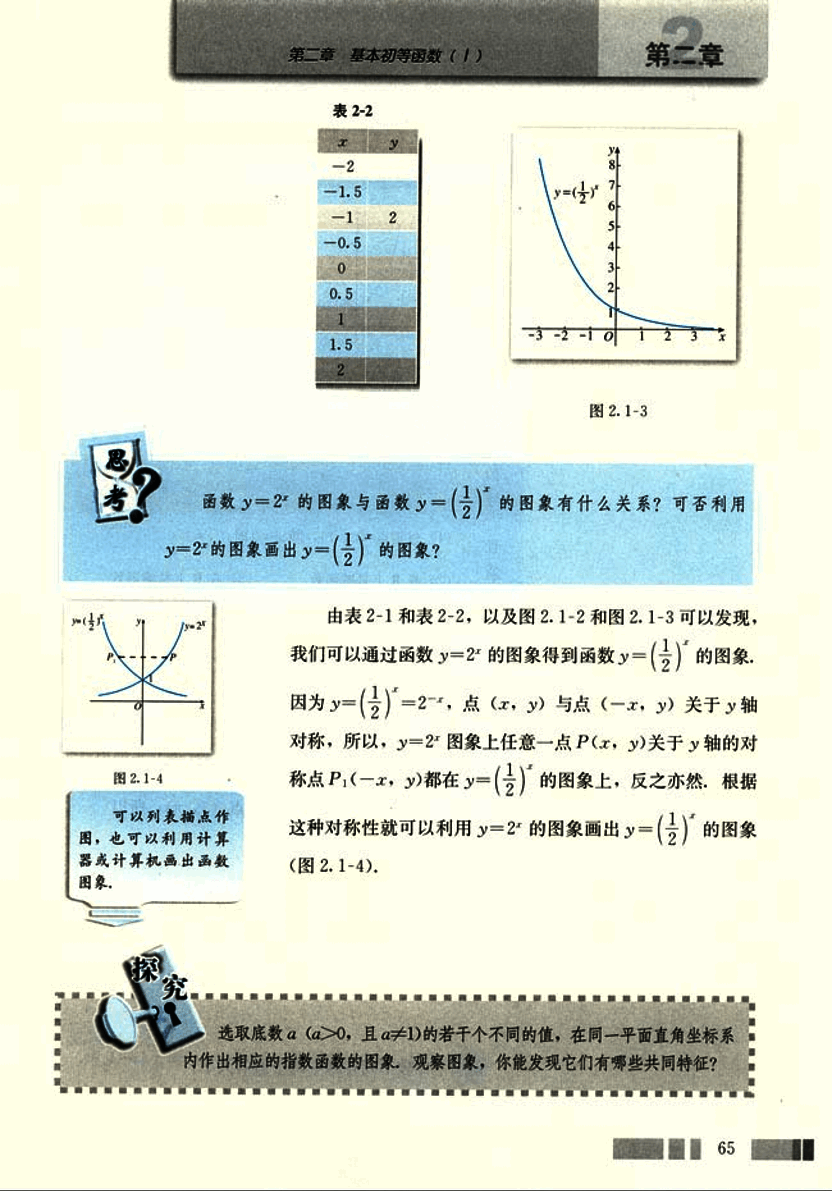
再画函数y = ( 1 2 ) x y = (\frac{1}{2})^x y = ( 2 1 ) x
请同学们完成x,y的对应值表2-2,并用描点法画出它的图像(图2.1-3)。
64
image
函数 y = 2 x y=2^x y = 2 x y = ( 1 2 ) x y=(\frac{1}{2})^x y = ( 2 1 ) x y = 2 x y=2^x y = 2 x y = ( 1 2 ) x y=(\frac{1}{2})^x y = ( 2 1 ) x
image
可以列表描点作图,也可以利用计算器或计算机画出函数图象。
由表 2-1 和表 2-2,以及图 2.1-2 和图 2.1-3 可以发现,我们可以通过函数 y = 2 x y=2^x y = 2 x y = ( 1 2 ) x y=(\frac{1}{2})^x y = ( 2 1 ) x
因为 y = ( 1 2 ) x = 2 − x y=(\frac{1}{2})^x = 2^{-x} y = ( 2 1 ) x = 2 − x ( x , y ) (x, y) ( x , y ) ( − x , y ) (-x, y) ( − x , y ) y = 2 x y=2^x y = 2 x y = ( 1 2 ) x y=(\frac{1}{2})^x y = ( 2 1 ) x y = 2 x y=2^x y = 2 x y = ( 1 2 ) x y=(\frac{1}{2})^x y = ( 2 1 ) x
选取底数 a a a a > 0 a>0 a > 0 a ≠ 1 a≠1 a = 1
65
普通高中课程标准实验教科书 数学 1
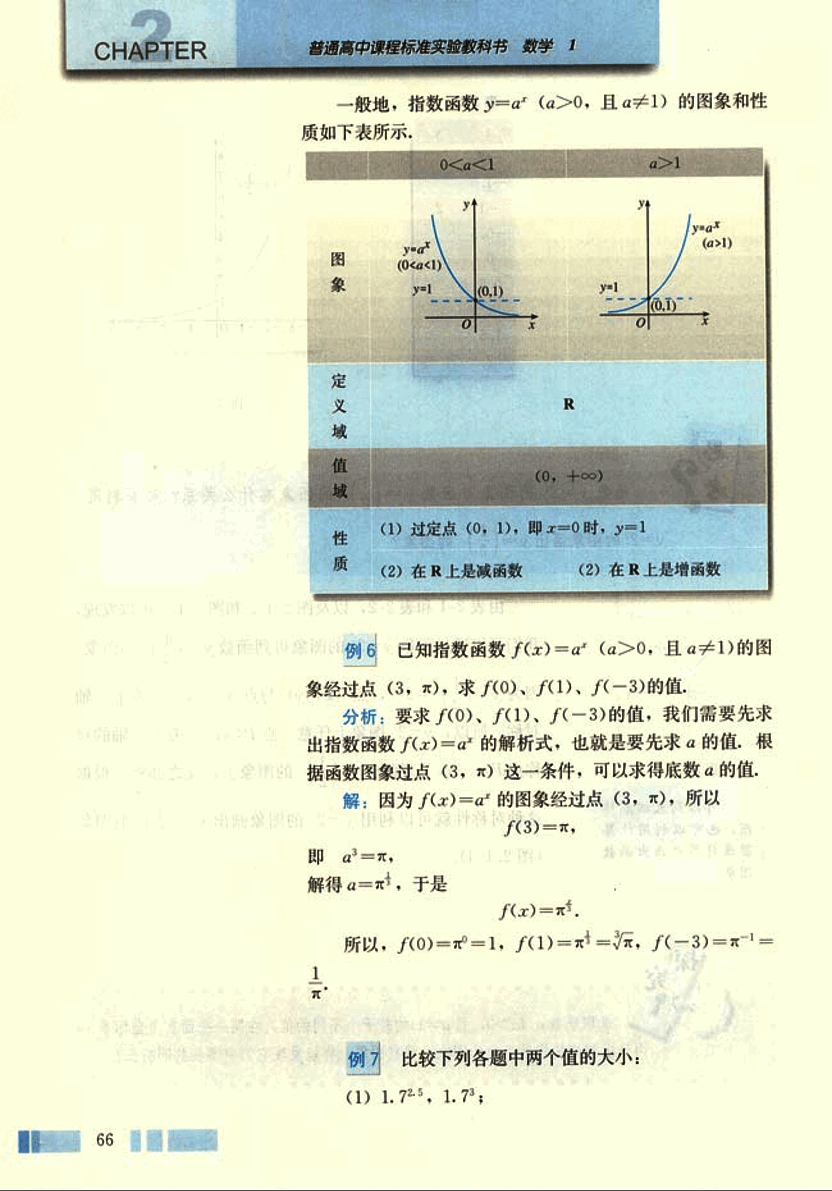
0 < a < 1 0 < a < 1 0 < a < 1 a > 1 a > 1 a > 1 图像 image image 定义域 R R 值域 ( 0 , + ∞ ) (0, +\infty) ( 0 , + ∞ ) ( 0 , + ∞ ) (0, +\infty) ( 0 , + ∞ ) 性质 (1) 过定点 (0, 1), 即 x = 0 x = 0 x = 0 y = 1 y = 1 y = 1 (2) 在 R 上是增函数
已知指数函数 f ( x ) = a x f(x) = a^x f ( x ) = a x a > 0 a > 0 a > 0 a ≠ 1 a \ne 1 a = 1 ( 3 , π ) (3, \pi) ( 3 , π ) f ( 0 ) f(0) f ( 0 ) f ( 1 ) f(1) f ( 1 ) f ( − 3 ) f(-3) f ( − 3 )
分析: 要求 f ( 0 ) f(0) f ( 0 ) f ( 1 ) f(1) f ( 1 ) f ( − 3 ) f(-3) f ( − 3 ) f ( x ) = a x f(x) = a^x f ( x ) = a x a a a ( 3 , π ) (3, \pi) ( 3 , π ) a a a
解: 因为 f ( x ) = a x f(x) = a^x f ( x ) = a x ( 3 , π ) (3, \pi) ( 3 , π ) f ( 3 ) = π f(3) = \pi f ( 3 ) = π a 3 = π a^3 = \pi a 3 = π a = π 3 a = \sqrt[3]{\pi} a = 3 π f ( x ) = ( π 3 ) x f(x) = (\sqrt[3]{\pi})^x f ( x ) = ( 3 π ) x
所以,f ( 0 ) = π 0 = 1 f(0) = \pi^0 = 1 f ( 0 ) = π 0 = 1 f ( 1 ) = π 3 f(1) = \sqrt[3]{\pi} f ( 1 ) = 3 π f ( − 3 ) = π − 1 = 1 π f(-3) = \pi^{-1} = \frac{1}{\pi} f ( − 3 ) = π − 1 = π 1
比较下列各题中两个值的大小:
(1) 1.7 2.5 1.7^{2.5} 1. 7 2.5 1.7 3 1.7^3 1. 7 3
(2) 0.8-0.1 , 0.8-0.2 ;
(3) 1.70.3 , 0.93.1 .
解:(1) 1.72.5 , 1.73 可看作函数 y = 1.7x 的两个函数值,由于底数 1.7 > 1,所以指数函数 y = 1.7x 在 R 上是增函数.
因为 2.5 < 3,所以 1.72.5 < 1.73 .
(2) 0.8-1 , 0.8-0.2 可看作函数 y = 0.8x 的两个函数值,由于底数 0 < 0.8 < 1,所以指数函数 y = 0.8x 在 R 上是减函数.
因为 -0.1 > -0.2,所以 0.8-0.1 < 0.8-0.2 .
(3) 因为 1.70.3 , 0.93.1 不能看作同一个指数函数的两个函数值,所以我们可以首先在这两个数值中间找一个数值,将这一个数值与原来两个数值分别比较大小,然后确定原来两个数值的大小关系.
由指数函数的性质知
1.70.3 > 1.70 = 1,
0.93.1 < 0.90 = 1,
所以 1.70.3 > 0.93.1 .
截止到 1999 年底,我国人口约 13 亿,如果今后能将人口年平均增长率控制在 1%,那么经过 20 年后,我国人口数最多为多少(精确到亿)?
解:设今后人口年平均增长率为 1%,经过 x 年后,我国人口数为 y 亿.
1999 年底,我国人口约为 13 亿;
经过 1 年(即 2000 年),人口数为
13 + 13 × 1% = 13 × (1 + 1%)(亿);
经过 2 年(即 2001 年),人口数为
13 × (1 + 1%) + 13 × (1 + 1%) × 1%
= 13 × (1 + 1%)2 (亿);
经过 3 年(即 2002 年),人口数为
13 × (1 + 1%)2 + 13 × (1 + 1%)2 × 1%
= 13 × (1 + 1%)3 (亿);
……
所以,经过 x 年,人口数为
67
普通高中课程标准实验教科书 数学 1
y = 13 × ( 1 + 1 % ) x = 13 × 1.01 x ( 亿 ) y = 13 \times (1+1\%)^x = 13 \times 1.01^x (亿) y = 13 × ( 1 + 1% ) x = 13 × 1.0 1 x ( 亿 )
当 x = 20 x = 20 x = 20 y = 13 × 1.01 20 ≈ 16 ( 亿 ) y = 13 \times 1.01^{20} \approx 16 (亿) y = 13 × 1.0 1 20 ≈ 16 ( 亿 )
所以,经过 20 年后,我国人口数最多为 16 亿。
在实际问题中,经常会遇到类似例 8 的指数增长模型:
设原有量为 N,平均增长率为 p,则对于经过时间 x 后的总量 y 可以用 y = N ( 1 + p ) x y = N(1+p)^x y = N ( 1 + p ) x y = k a x ( k ∈ R , a > 0 , 且 a ≠ 1 ) y = ka^x (k \in R, a > 0, 且 a \ne 1) y = k a x ( k ∈ R , a > 0 , 且 a = 1 )
(1) 如果人口年均增长率提高 1 个百分点,利用计算器分别计算 20 年,33 年后我国的人口数。
(2) 如果年均增长率保持在 2%,利用计算器计算 2020~2100 年,每隔 5 年相应的人口数。
(3) 你看到我国人口数的增长呈现什么趋势?
(4) 你是如何看待我国的计划生育政策的?
在同一平面直角坐标系中画出下列函数的图像: (1) y = 3 x y = 3^x y = 3 x
(2) y = ( 1 3 ) x y = (\frac{1}{3})^x y = ( 3 1 ) x
求下列函数的定义域: (1) y = x 3 y = \sqrt[3]{x} y = 3 x
(2) y = ( 1 2 ) x y = (\frac{1}{2})^x y = ( 2 1 ) x
某种细胞分裂时,由 1 个分裂成 2 个,2 个分裂成 4 个……依此类推,写出 1 个这样的细胞分裂 x 次后,得到的细胞个数 y 与 x 的函数解析式。 image
求下列各式的值:100 \sqrt{100} 100 ( − 0.1 ) 2 \sqrt{(-0.1)^2} ( − 0.1 ) 2 ( π − 4 ) 2 \sqrt{(\pi - 4)^2} ( π − 4 ) 2 ( x − y ) 2 \sqrt{(x-y)^2} ( x − y ) 2 x > y x>y x > y
用分数指数幂表示下列各式 (其中各字母均为正数):b 2 a a 3 b \sqrt{\frac{b^2}{a}\sqrt{a^3b}} a b 2 a 3 b a 3 a a a \sqrt{a^3\sqrt{a}}\sqrt{a\sqrt{a}} a 3 a a a m ⋅ m ⋅ m ( m ) 3 ⋅ m \frac{\sqrt{m}\cdot\sqrt{m}\cdot\sqrt{m}}{(\sqrt{m})^3\cdot m} ( m ) 3 ⋅ m m ⋅ m ⋅ m
用计算器求值 (结果保留 4 位有效数字):5 1 3 5^\frac{1}{3} 5 3 1 8.3 1 3 8.3^\frac{1}{3} 8. 3 3 1 3 2 5 3^\frac{2}{5} 3 5 2 2 1 7 2^\frac{1}{7} 2 7 1
计算下列各式的值 (式中各字母均为正数):a 2 ⋅ a 4 ÷ a 3 a^2\cdot a^4\div a^3 a 2 ⋅ a 4 ÷ a 3 a 2 ÷ a 4 ÷ a 2 a^2\div a^4\div a^2 a 2 ÷ a 4 ÷ a 2 ( x y ) 1 2 (xy)^\frac{1}{2} ( x y ) 2 1 4 a 3 b 6 ÷ ( − 2 3 a − 1 b − 4 ) 4a^3b^6\div(-\frac{2}{3}a^{-1}b^{-4}) 4 a 3 b 6 ÷ ( − 3 2 a − 1 b − 4 ) ( 16 x − 6 25 y 4 ) − 1 2 \left(\frac{16x^{-6}}{25y^4}\right)^{-\frac{1}{2}} ( 25 y 4 16 x − 6 ) − 2 1 ( − 2 x 2 + y 4 ) ( 3 x 2 + y 4 ) ( − 4 x 4 y 4 ) (-2x^2+y^4)(3x^2+y^4)(-4x^4y^4) ( − 2 x 2 + y 4 ) ( 3 x 2 + y 4 ) ( − 4 x 4 y 4 ) ( 2 x + 3 y ) ( 2 x − 3 y ) (2x+3y)(2x-3y) ( 2 x + 3 y ) ( 2 x − 3 y ) 4 x 2 ( − 3 x 3 y 4 ) ÷ ( − 6 x 4 y 3 ) 4x^2(-3x^3y^4)\div(-6x^4y^3) 4 x 2 ( − 3 x 3 y 4 ) ÷ ( − 6 x 4 y 3 )
求下列函数的定义域:y = 2 x − 2 y = 2^{x-2} y = 2 x − 2 y = 3 2 x + 1 y = 3^{2x+1} y = 3 2 x + 1 y = ( 1 2 ) x 2 y = \left(\frac{1}{2}\right)^{\frac{x}{2}} y = ( 2 1 ) 2 x y = 0.7 x y = 0.7^x y = 0. 7 x
一种产品的产量原来是 a a a m m m p % p\% p %
比较下列各题中两个数的大小:3 0.8 3^{0.8} 3 0.8 3 0.7 3^{0.7} 3 0.7 0.75 − 0.1 0.75^{-0.1} 0.7 5 − 0.1 0.75 0.1 0.75^{0.1} 0.7 5 0.1 1.01 2.7 1.01^{2.7} 1.0 1 2.7 1.01 2.5 1.01^{2.5} 1.0 1 2.5 0.99 3.3 0.99^{3.3} 0.9 9 3.3 0.99 4.5 0.99^{4.5} 0.9 9 4.5
已知下列不等式,比较 m m m n n n 2 m < 2 n 2^m < 2^n 2 m < 2 n 0.2 m < 0.2 n 0.2^m < 0.2^n 0. 2 m < 0. 2 n a m < a n a^m < a^n a m < a n 0 < a < 1 0 < a < 1 0 < a < 1 a m > a n a^m > a^n a m > a n a > 1 a > 1 a > 1
69
当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了。 (1) 死亡生物组织内的碳14经过九个“半衰期”后,用一般的放射性探测器能测到碳14吗?
(2) 大约经过多少万年后,用一般的放射性探测器就测不到碳14了(精确到万年)?
按复利计算利息的一种储蓄,本金为 a 元,每期利率为 r ,设本利和为 y ,存期为 x ,写出本利和 y 随存期变化的函数解析式,如果存入本金 1000 元,每期利率为 2.25%,试计算 5 期后的本利和是多少(精确到 1 元)?
家用电器(如空调)使用的氟化物的释放破坏了大气上层的臭氧层,臭氧含量 Q 呈指数型函数变化,满足关系式 Q = Q 0 e − 0.0025 t Q = Q_0e^{-0.0025t} Q = Q 0 e − 0.0025 t Q 0 Q_0 Q 0
(1) 100 年后,臭氧含量约为初始量的多少?
(2) 随时间的增加,臭氧的含量是增加还是减少?
设 y 1 = a x + 1 y_1 = a^{x+1} y 1 = a x + 1 y 2 = a x 2 y_2 = a^{x^2} y 2 = a x 2 a > 0 a > 0 a > 0 a ≠ 1 a \ne 1 a = 1 x 为何值时,有: (1) y 1 = y 2 y_1 = y_2 y 1 = y 2
(2) y 1 > y 2 y_1 > y_2 y 1 > y 2
求不等式 a x + 1 > a x − 1 a^{x+1} > a^{x-1} a x + 1 > a x − 1 a > 0 a > 0 a > 0 a ≠ 1 a \ne 1 a = 1 x 的取值范围。
已知 x + 1 x = 3 x + \frac{1}{x} = 3 x + x 1 = 3
(1) x 2 + 1 x 2 x^2 + \frac{1}{x^2} x 2 + x 2 1
(2) x 3 + 1 x 3 x^3 + \frac{1}{x^3} x 3 + x 3 1
(3) x 3 − 1 x 3 x^3 - \frac{1}{x^3} x 3 − x 3 1
(4) x 4 − 1 x 4 x^4 - \frac{1}{x^4} x 4 − x 4 1
指数函数 y = ( 1 2 ) x y = \left(\frac{1}{2}\right)^x y = ( 2 1 ) x y = a x 2 + b x y = ax^2 + bx y = a x 2 + b x image
当某种药品注射到身体内,它在血液中的残余量呈指数型函数衰减。 (1) 药品 S 在血液中的残余量可以用以下指数型函数描述:
y = 5 e − 0.2 t y = 5e^{-0.2t} y = 5 e − 0.2 t
其中,t 是注射一剂药 S 后的时间(单位:h),y 是药品 S 在人体内的残余量(单位:mg)。
a. y 的初始值是什么?
b. 当 t = 10 t = 10 t = 10 y 的值是多少?
c. 画出这个函数的图象。
(2) 另一种药品在身体中的残余量可以表示成 y = 5 e − 0.1 x y = 5e^{-0.1x} y = 5 e − 0.1 x
70
指数函数 y = a x y = a^x y = a x a > 0 a > 0 a > 0 a ≠ 1 a \ne 1 a = 1
用信息技术绘制函数 y = a x y = a^x y = a x a > 0 a > 0 a > 0 a ≠ 1 a \ne 1 a = 1 a a a x A x_A x A
如图 1,从左向右拖动点 A (0 < x A < 1 0 < x_A < 1 0 < x A < 1 x A x_A x A x A x_A x A x A = 1 x_A = 1 x A = 1 x A > 1 x_A > 1 x A > 1 x A x_A x A
图1 图2
从图 1、2 可以容易地发现指数函数的性质: (1) 所有的函数图象都过点 (0, 1);− ∞ -\infty − ∞ + ∞ +\infty + ∞ + ∞ +\infty + ∞ 0 < a < 1 0 < a < 1 0 < a < 1 a > 1 a > 1 a > 1
接下来请你继续观察图 1 和图 2,探究以下问题:
当自变量 x 取同一个数时,对应的函数值 y 的大小关系是什么,从中你发现了什么规律?
你可以亲自动手用信息技术绘制指数函数的图象,通过改变 a 的大小,认识指数函数的变化规律。
71
84