1.1 空间几何体的结构
1.1 空间几何体的结构
15
CHAPTER 1.1 空间几何体的结构
观察
观察下面的图片,这些图片中的物体具有什么几何结构特征?你能对它们进行分类吗?分类依据是什么?
(1) (2) (3) (4)
(5) (6) (7) (8)
(9) (10) (11) (12)
(13) (14) (15) (16)
图 1.1-1

16
第一章 空间几何体
1.1.1 柱、锥、台、球的结构特征
- 棱柱的结构特征
图 1.1-1 中的 (2) 是我们非常熟悉的长方体包装盒,它的每个面都是平行四边形(矩形),并且相对的两个面给我们以平行的形象,如同天花板与地面一样。
如图 1.1-2,一般地,有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱 (prism)。棱柱中,两个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧面与底面的公共顶点叫做棱柱的顶点。底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱……我们用表示底面各顶点的字母表示棱柱,图 1.1-2 的棱柱,表示为棱柱 ABCDEF-A'B'C'D'E'F'。
图 1.1-1 中的 (5)、(7)、(9) 都是具有棱柱结构的物体。
- 棱锥的结构特征
图 1.1-1 中的 (14) 和 (15) 这样的几何体,均由平面图形围成,其中一个面是多边形,其余各面都是三角形,并且这些三角形有一个公共顶点。
如图 1.1-3,一般地,有一个面是多边形,其余各面都
3

17
CHAPTER
普通高中课程标准实验教科书 数学 2
是有一个公共顶点的三角形,由这些面所围成的几何体叫做
棱锥(pyramid),这个多边形面叫做棱锥的底面或底;有公共
顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做
棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱,底面是三角
形、四边形、五边形………………的棱锥分别叫做三棱锥、四棱锥、五
棱锥………………其中三棱锥又叫四面体,棱锥也用表示顶点和底面各
顶点的字母表示,图1.1-3的四棱锥,表示为棱锥S-ABCD.
思考?
如何描述图1.1-1中(1)与(8)的几何结构特征?
3. 圆柱的结构特征
如图1.1-4,以矩形的一边所在直线为旋转轴,其余三
边旋转形成的曲面所围成的几何体叫做圆柱(circular cylin-
der)。旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面
叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的
侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧
面的母线。
在生活中,许多容器和物体都是圆柱形的,如图1.1-1
中的(1)和(8)。圆柱用表示它的轴的字母表示,图1.1-4
中圆柱表示为圆柱OO。
圆柱和棱柱统称为柱体。
4. 圆锥的结构特征
与圆柱一样,圆锥也可以看作是由平面图形旋转而成
的,如图1.1-5,以直角三角形的一条直角边所在直线为旋
转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥
(circular cone)。图1.1-1中的(3)和(6)就是圆锥形物
体。圆锥也有轴、底面、侧面和母线。
探究
请你仿照圆柱中关于轴、底面、侧面、母线的定义,在图
1.1-5 中标出圆锥的轴、底面、侧面和母线,
4

18
第一章 空间几何体
第一章
圆锥也用表示它的轴的字母表示,图1.1-5中的圆锥表示为圆锥SO。
圆锥与棱锥统称为锥体。
5. 棱台与圆台的结构特征
如何描述图1.1-1中(4)、(10)、(13)、(16)的几何结构特征,它们与锥体有何关系?
我们已经学过柱体和锥体,但是具有图1.1-1中像(4)、(10)、(13)、(16)这种结构的几何体我们没有学过。像(13)和(16)这样的几何体,是用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的几何体(图1.1-6)叫做棱台(frustum of a pyramid)。原棱锥的底面和截面分别叫做棱台的下底面和上底面,棱台也有侧面、侧棱、顶点。
探究
请仿照棱锥中关于侧面、侧棱、顶点的定义,在图1.1-6中标出棱台的侧面、侧棱、顶点。
由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……与棱柱的表示一样,图1.1-6中的棱台表示为棱台ABCD-A'B'C'D'。
图1.1-1中像(4)和(10)这样的几何体,是用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,这样的几何体(图1.1-7)叫做圆台(frustum of a cone)。
与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线。请你在图1.1-7中标出它们,并用字母将图1.1-7中的圆台表示出来。
棱台与圆台统称为台体。
5

19
CHAPTER
普通高中课程标准实验教科书 数学 2
探究
圆柱可以由矩形旋转得到,圆锥可以由直角三角形旋转得到,
圆台可以由什么图形旋转得到?如何旋转?
6. 球的结构特征
如图 1.1-8,以半圆的直径所在直线为旋转轴,半圆面
旋转一周形成的几何体叫做球体 (solid sphere),简称球。
半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆
的直径叫做球的直径。图 1.1-1 中的 (11)、(12) 具有球体
的几何结构特征。球常用表示球心的字母 O 表示,图 1.1-8
中的球表示为球 O。
棱台与棱柱、棱锥有什么关系?圆台与圆柱、圆锥呢?
1.1.2 简单组合体的结构特征
从整体看,下列物体表示的几何体不属于前面学习过的任何一种
几何体,我们如何描述它们的结构特征呢?
图 1.1-9
20
第一章 空间几何体
第一章
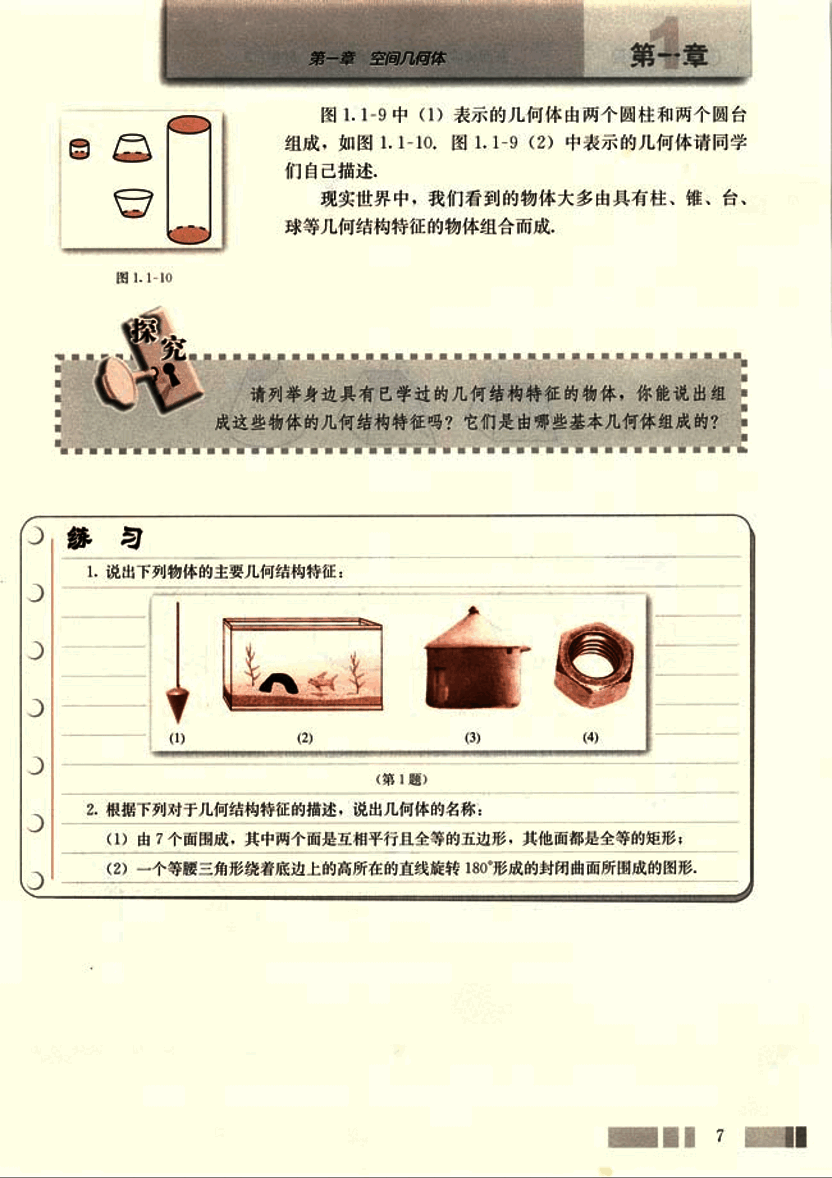
图 1.1-9 中 (1) 表示的几何体由两个圆柱和两个圆台组成,如图 1.1-10。图 1.1-9 (2) 中表示的几何体请同学们自己描述。
现实世界中,我们看到的物体大多由具有柱、锥、台、球等几何结构特征的物体组合而成。
请列举身边具有已学过的几何结构特征的物体,你能说出组成这些物体的几何结构特征吗?它们是由哪些基本几何体组成的?
练习
- 说出下列物体的主要几何结构特征:
(1) image1 (2) image2 (3) image3 (4) image4
(第1题)
- 根据下列对于几何结构特征的描述,说出几何体的名称:
(1) 由 7 个面围成,其中两个面是互相平行且全等的五边形,其他面都是全等的矩形;
(2) 一个等腰三角形绕着底边上的高所在的直线旋转 180° 形成的封闭曲面所围成的图形。
7
21
CHAPTER
普通高中课程标准实验教科书 数学 2
习题1.1
A组
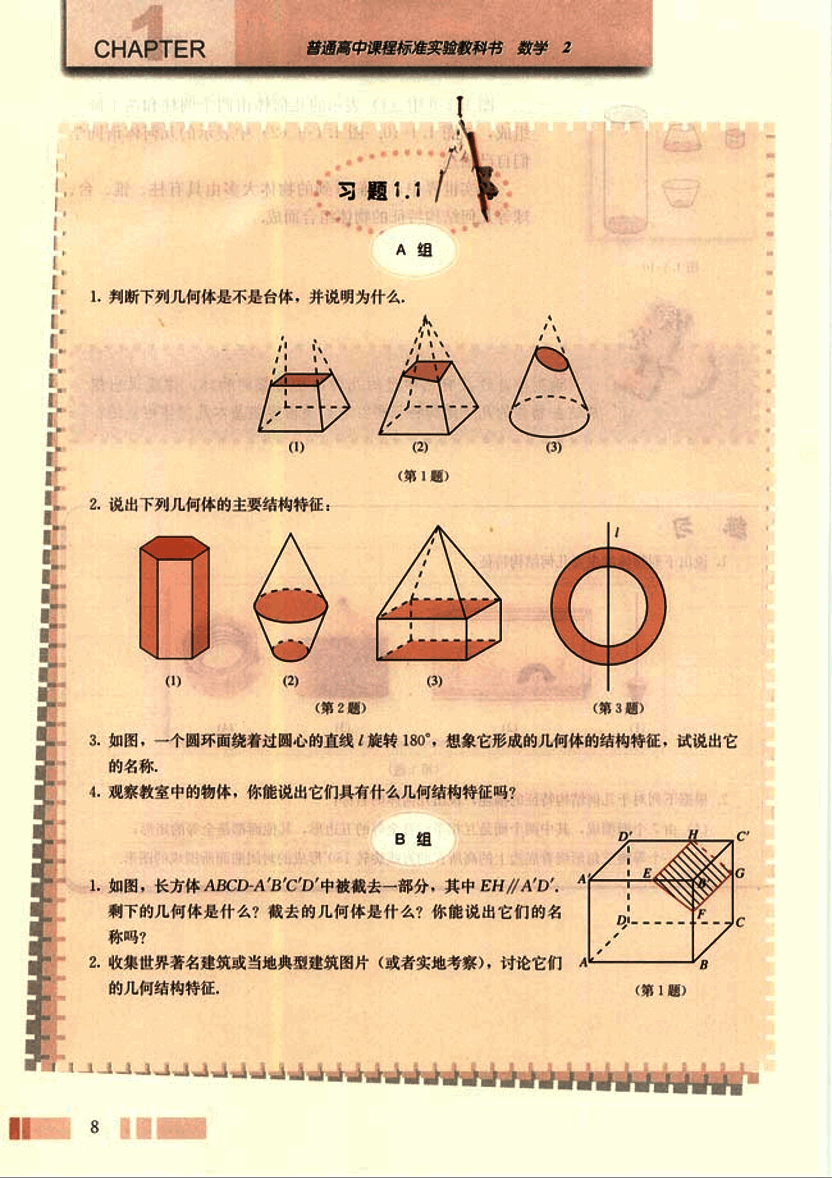
- 判断下列几何体是不是台体,并说明为什么。
(1) (2) (3)
(第1题)
- 说出下列几何体的主要结构特征:
(1) (2) (3) (第3题)
(第2题)
如图,一个圆环面绕着过圆心的直线 l 旋转 180°,想象它形成的几何体的结构特征,试说出它的名称。
观察教室中的物体,你能说出它们具有什么几何结构特征吗?
B组
如图,长方体 ABCD-A'B'C'D' 中被截去一部分,其中 EH//A'D'. 剩下的几何体是什么?截去的几何体是什么?你能说出它们的名字吗?
收集世界著名建筑或当地典型建筑图片(或者实地考察),讨论它们的几何结构特征.
(第1题)