1.3 空间几何体的表面积与体积
1.3 空间几何体的表面积与体积
34
1.3 空间几何体的表面积与体积
空间几何体的度量是几何研究的重要内容之一,度量主要包括长度、角度、面积、体积等等。本节我们学习空间几何体的表面积和体积,表面积是几何体表面的面积,它表示几何体表面的大小;体积是几何体所占空间的大小。
1.3.1 柱体、锥体、台体的表面积与体积
1. 柱体、锥体、台体的表面积
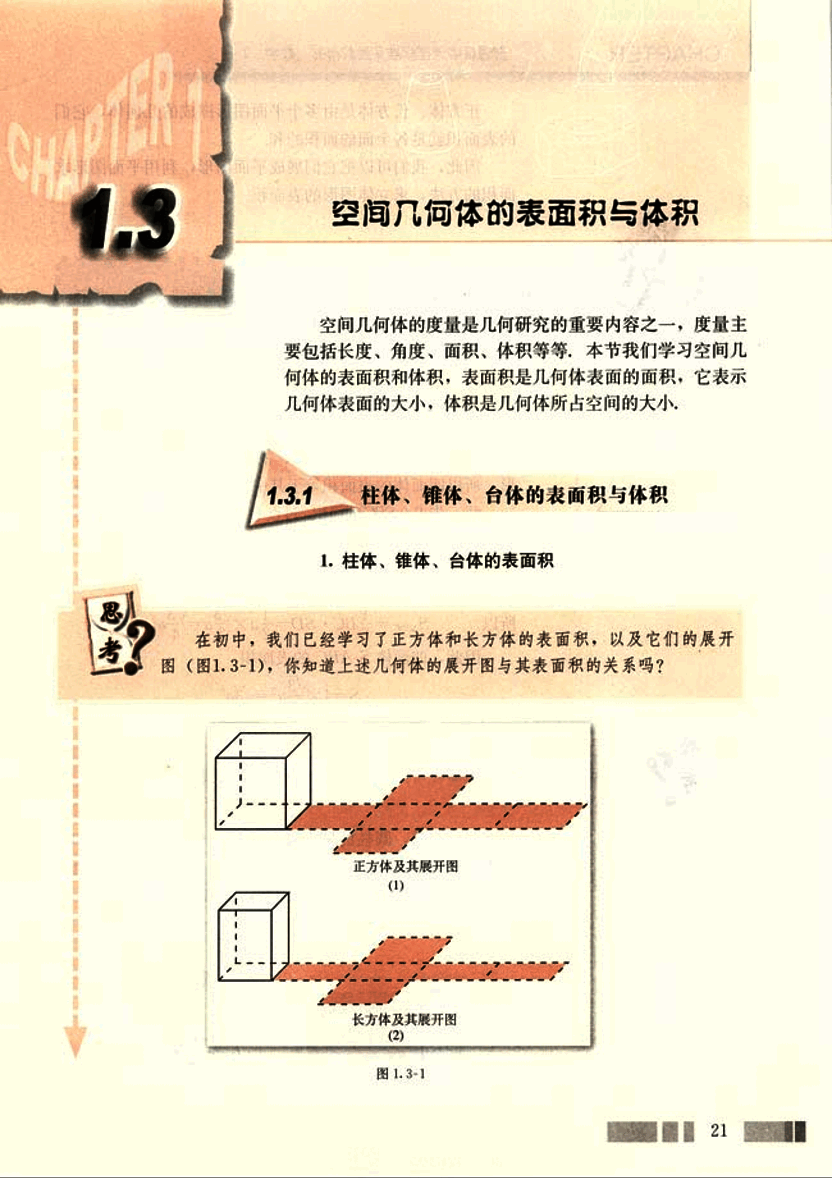
在初中,我们已经学习了正方体和长方体的表面积,以及它们的展开图(图1.3-1),你知道上述几何体的展开图与其表面积的关系吗?
图 1.3-1
21
35
CHAPTER
探究
正方体、长方体是由多个平面图形围成的几何体,它们
的表面积就是各个面的面积的和。
因此,我们可以把它们展成平面图形,利用平面图形求
面积的方法,求立体图形的表面积。
棱柱、棱锥、棱台也是由多个平面图形围成的几何体,它们
的展开图是什么?如何计算它们的表面积?
例1
已知棱长为 a,各面均为等边三角形的四面体
S-ABC(图 1.3-2),求它的表面积。
分析: 由于四面体 S-ABC 的四个面是全等的等边三角
形,所以四面体的表面积等于其中任何一个面面积的 4 倍。
解: 先求△SBC 的面积,过点 D 作 SD⊥BC,交 BC 于点 D。
因为 BC=a,
所以
。
所以
。
因此,四面体 S-ABC 的表面积
。
思考
如何根据圆柱、圆锥的几何结构特征,求它们的表面积?
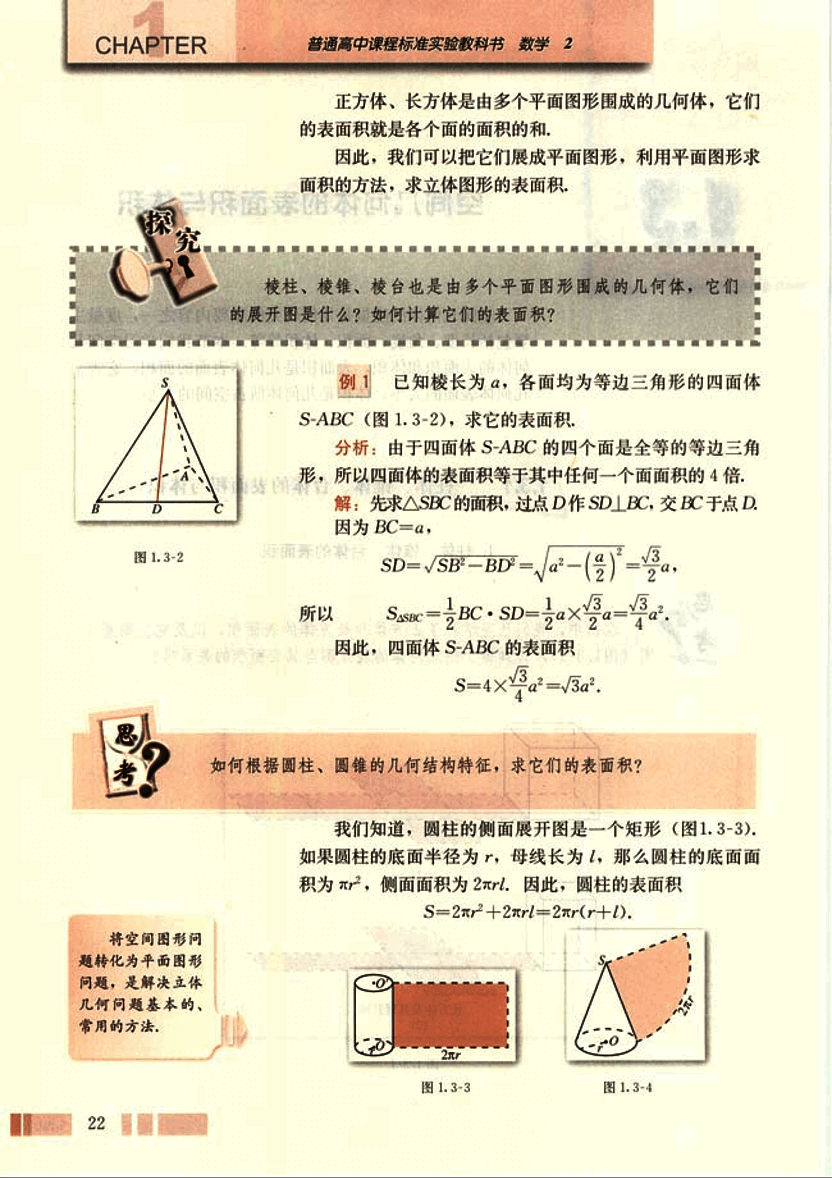
我们知道,圆柱的侧面展开图是一个矩形(图 1.3-3)。
如果圆柱的底面半径为 r,母线长为 l,那么圆柱的底面面
积为 πr²,侧面面积为 2πrl。因此,圆柱的表面积
。
将空间图形问题
转化为平面图形
问题,是解决立体
几何问题基本的、
常用的方法。
36
第一章 空间几何体
圆锥的表面积
圆锥的侧面展开图是一个扇形(图1.3-4)。如果圆锥的底面半径为 r,母线长为 l,那么它的表面积
.
(1) 联系圆柱和圆锥的展开图,你能想象圆台展开图的形状,并且画出它吗?
(2) 如果圆台的上、下底面半径分别为 r, r’,母线长为 l,你能计算出它的表面积吗?
圆台的表面积
圆台的侧面展开图是一个扇环(图1.3-5),它的表面积等于上、下两个底面的面积和加上侧面的面积,即
.
例2 如图1.3-6,一个圆台形花盆盆口直径为20 cm,盆底直径为15 cm,底部渗水圆孔直径为1.5 cm,盆壁长15 cm,那么花盆的表面积约是多少平方厘米(π取3.14,结果精确到1 cm²)?
分析: 花盆的表面积等于花盆的侧面面积加上底面面积,再减去底面圆孔的面积。
解: 如图1.3-6,由圆台的表面积公式得花盆的表面积
.
答: 花盆的表面积约是999 cm².
柱体、锥体与台体的体积
我们已经学习了计算特殊的棱柱——正方体、长方体,以及圆柱的体积公式,它们的体积公式可以统一为
(S为底面面积,h为高),
一般棱柱的体积也是
,
其中S为底面面积,h为棱柱的高。
23

37
CHAPTER
普通高中课程标准实验教科书 数学 2
圆锥的体积公式是
(S为底面面积,h为高),
它是同底等高的圆柱的体积的。
探究棱锥与同底等高的棱柱体积之间的关系。
经过探究可以得到,棱锥的体积也是同底等高的棱柱体积的,即棱锥的体积
(S为底面面积,h为高)。
由此可见,棱柱与圆柱的体积公式类似,都是底面面积乘高;棱锥与圆锥的体积公式类似,都是底面面积乘高的。
由于圆台(棱台)是由圆锥(棱锥)截成的,因此可以利用两个锥体的体积差,得到圆台(棱台)的体积公式
,
其中S', S分别为上、下底面面积,h为圆台(棱台)高。
思考
比较柱体、锥体、台体的体积公式:
(S为底面积,h为柱体高),
(S为底面积,h为锥体高),
(S', S分别为上、下底面面积,h为台体高)。
你能发现三者之间的关系吗?柱体、锥体是否可以看作“特殊”的台体?其体积公式是否可以看作台体体积公式的“特殊”形式?
24

38
第一章 空间几何体
例3
有一堆规格相同的铁制(铁的密度是 7.8 g/cm³)六角螺帽(图 1.3-7)共重 5.8 kg,已知底面是正六边形,边长为 12 mm,内孔直径为 10 mm,高为 10 mm,问这堆螺帽大约有多少个(π 取 3.14)?
解:六角螺帽的体积是六棱柱体积与圆柱体积的差,即
所以螺帽的个数为:
答:这堆螺帽大约有 252 个。
练习
已知圆锥的表面积为 a m²,且它的侧面展开图是一个半圆,求这个圆锥的底面直径。
右图是一种机器零件,零件下面是六棱柱(底面是正六边形,侧面是全等的矩形)形,上面是圆柱(尺寸如图,单位:mm)形,电镀这种零件需要用锌,已知每平方米用锌 0.11 kg,问电镀 10 000 个零件需锌多少千克(结果精确到 0.01 kg)?第2题
棱台的两个底面面积分别是 245 cm² 和 80 cm²,截得这个棱台的棱锥的高为 35 cm,求这个棱台的体积。
1.3.2 球的体积和表面积
球既没有底面,也无法像柱体、锥体和台体那样展成平面图形,怎样求球的表面积与体积呢?
25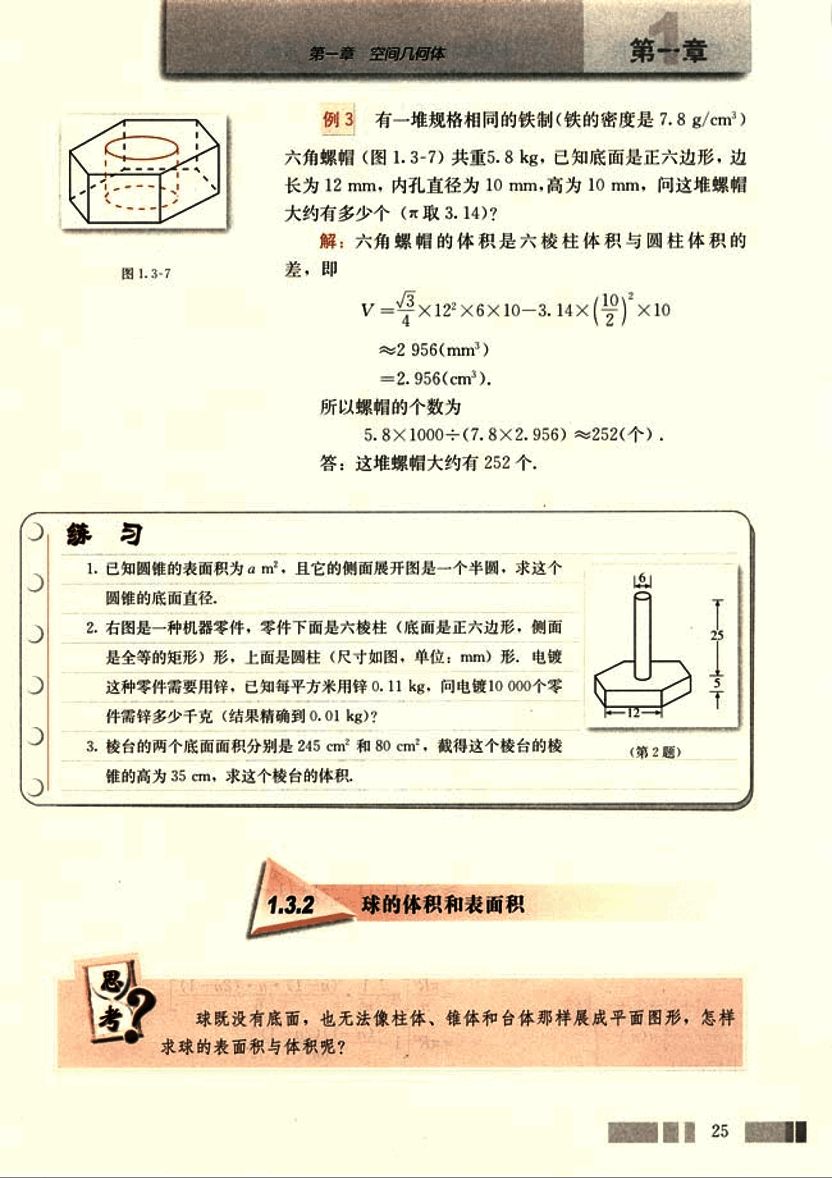
39
CHAPTER 1. 球的体积
设球的半径为 R,它的体积只与半径 R 有关,是以 R 为自变量的函数。
如图 1.3-8,将半径 OA n 等分,过这些等分点作平面,把半球切割成 n 层,每一层都是近似于圆柱形状的“小圆片”,这些“小圆片”的体积之和就是半球的体积。
由于“小圆片”近似于圆柱形状,所以它的体积也近似于相应的圆柱的体积,它的高就是“小圆片”的厚度 ,底面就是“小圆片”的下底面。
由勾股定理可得第 i 层(由下向上数)“小圆片”的下底面半径
, (i = 1, 2, ..., n)
于是,第 i 层“小圆片”的体积
, (i = 1, 2, ..., n)
半球的体积
26

40
第一章 空间几何体
第一章
所以 ①
容易看出,当所分层数不断增加,也就是说,当 不断变大时,①式越来越接近半球的体积,如果 无限变大,就能由①式推出 的值。
事实上,随着 增大, 越来越小,如 时,; 时,;……当 无限变大时, 趋向于 0。这时,由①式推出
所以半径为 R 的球的体积
在球的体积公式的推导过程中,我们使用了“分割、求近似值、再由近似值转化为球的体积”的方法:即先将半径 等分;再求出每一部分体积的近似值,并将这些近似值相加,得出半球的近似体积;当 无限变大时,就可得到半球的体积。这种重要的数学方法,后面推导球的表面积时,我们还会运用它。
例 4
某街心花园有许多钢球(钢的密度是 7.9 g/cm³),每个钢球重 145 kg,并且外径等于 50 cm,试根据以上数据,判断钢球是实心的还是空心的,如果是空心的,请你计算出它的内径(取 π≈3.14,结果精确到 1 cm)。
解:由于外径为 50 cm 的钢球的质量为
(g),
街心花园中钢球的质量为 145 000 g,而 145 000 < 517 054,所以钢球是空心的。
设球的内径是 2x cm,那么球的质量为
解得
27
41
CHAPTER
普通高中课程标准实验教科书 数学 2
2r ≈ 45 (cm)
答:钢球是空心的,其内径约为45 cm。
2. 球的表面积
设球的半径为 R,则它的表面积由半径 R 唯一确定,即它的表面积 S 也是以 R 为自变量的函数。
我们运用类似推导球体积公式的方法,推导球的表面积公式。
(1) 分割。如图 1.3-9,把球的表面分成 n 个“小球面片”,设它们的表面积分别是 S₁, S₂, …, Sn。那么,球的表面积
S = S₁ + S₂ + … + Sn
把球心 O 和每一个“小球面片”的顶点连接起来,整个球体就被分割成 n 个以这些“小球面片”为底,球心为顶点的“小锥体”。例如,球心与第 i 个“小球面片”顶点相连后,就得到一个以 O 为顶点,以第 i 个“小球面片”为底面的“小锥体”(图 1.3-9)。这样的“小锥体”的底面是球面的一部分,底面是“曲”的。如果每一个“小球面片”都非常小,那么“小锥体”的底面几乎是“平”的,这时,每一个“小锥体”就近似于棱锥,它们的高近似于球半径 R。
(2) 求近似和。设这 n 个“小锥体”的体积分别为 V₁, V₂, …, Vn。那么,球的体积
V = V₁ + V₂ + … + Vn
由于“小锥体”近似于棱锥,所以我们用相应棱锥的体积作为“小锥体”体积的近似值。第 i 个“小锥体”对应的棱锥以 O 为顶点,以 O 与第 i 个“小球面片”顶点的连线为棱。设它的高为 h,底面面积为 S'。于是,它的体积

42
第一章 空间几何体
第一节
这样就有
以及
①
(3) 转化为球的表面积,容易看出,分割得越细密,也
就是每一个“小球面片”越小,“小锥体”就越接近于棱锥。如果分割无限加细,每一个“小球面片”都无限变小,那么
就趋向于 R, 就趋向于 。于是,
我们由①式可以得出
我们已知
所以
即
例 5
图 1.3-10 表示一个用鲜花做成的花柱,它的下
面是一个直径为 1 m,高为 3 m 的圆柱形物体,上面是一个
半球形体。如果每平方米大约需要鲜花 150 朵,那么装饰这
个花柱大约需要多少朵鲜花(取 3.1)?
解:圆柱形物体的侧面面积
半球形物体的表面积为
所以
(朵)
答:装饰这个花柱大约需要 1635 朵鲜花。
29

43
CHAPTER 1
普通高中课程标准实验教科书 数学 2
本节我们学习了柱体、锥体、台体、球体的表面积与体积的计算方法,在生产、生活中我们遇到的物体,虽然形状往往比较复杂,但是很多物体都可以看作是由这些简单的几何体组合而成,它们的体积可以转化为这些简单几何体体积的和。
练习
- 将一个气球的半径扩大1倍,它的体积增大到原来的几倍?
- 一个正方体的顶点都在球面上,它的棱长是a cm,求球的体积。
- 一个球的体积是100 cm³,试计算它的表面积(取3.14,结果精确到1 cm²)。
习题 1.3
A组
- 五棱台的上、下底面均是正五边形,边长分别是8 cm和18 cm,侧面是全等的等腰梯形,侧棱长是13 cm,求它的侧面面积。
- 已知圆台的上下底面半径分别是r、R,且侧面面积等于两底面积之和,求圆台的母线长。
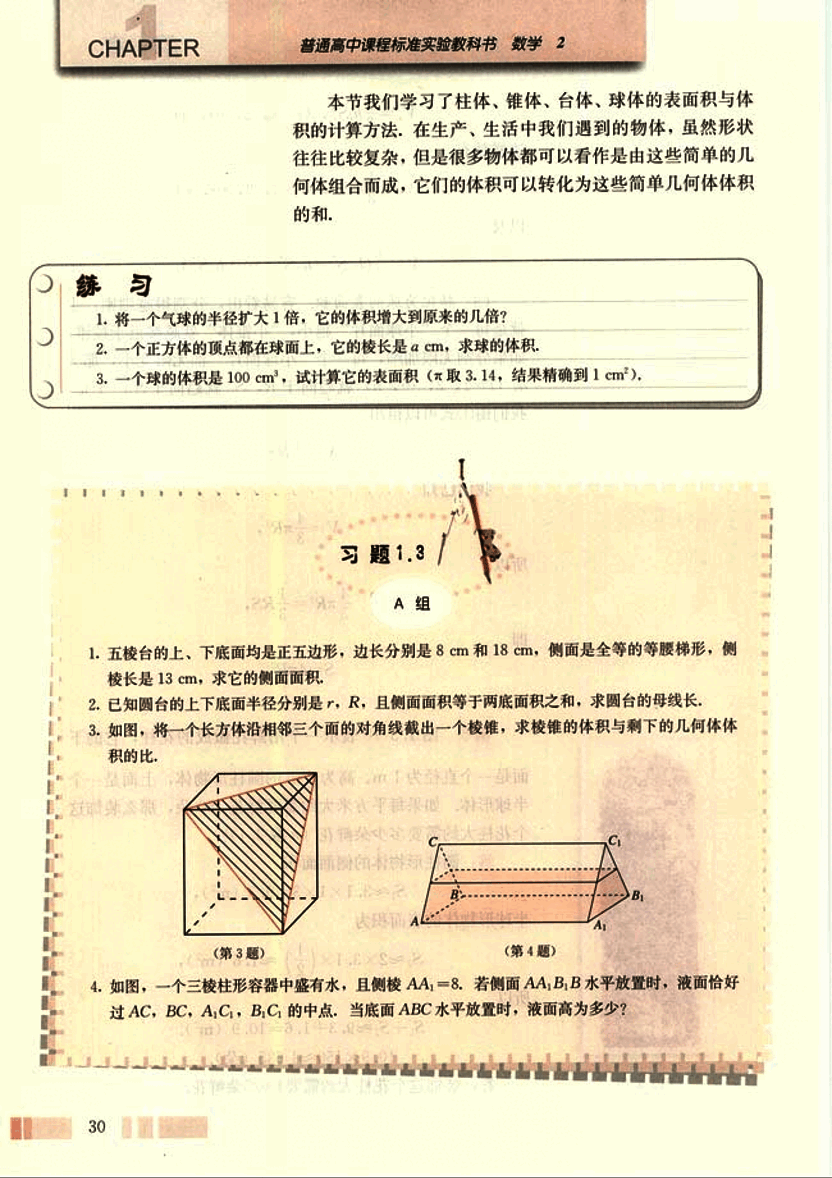
- 如图,将一个长方体沿相邻三个面的对角线截出一个棱锥,求棱锥的体积与剩下的几何体体积的比。
- 如图,一个三棱柱形容器中盛有水,且侧棱AA₁=8。若侧面AA₁B₁B水平放置时,液面恰好过AC、BC、A₁C₁、B₁C₁的中点,当底面ABC水平放置时,液面高为多少?
30
44
第一章 空间几何体
第一章
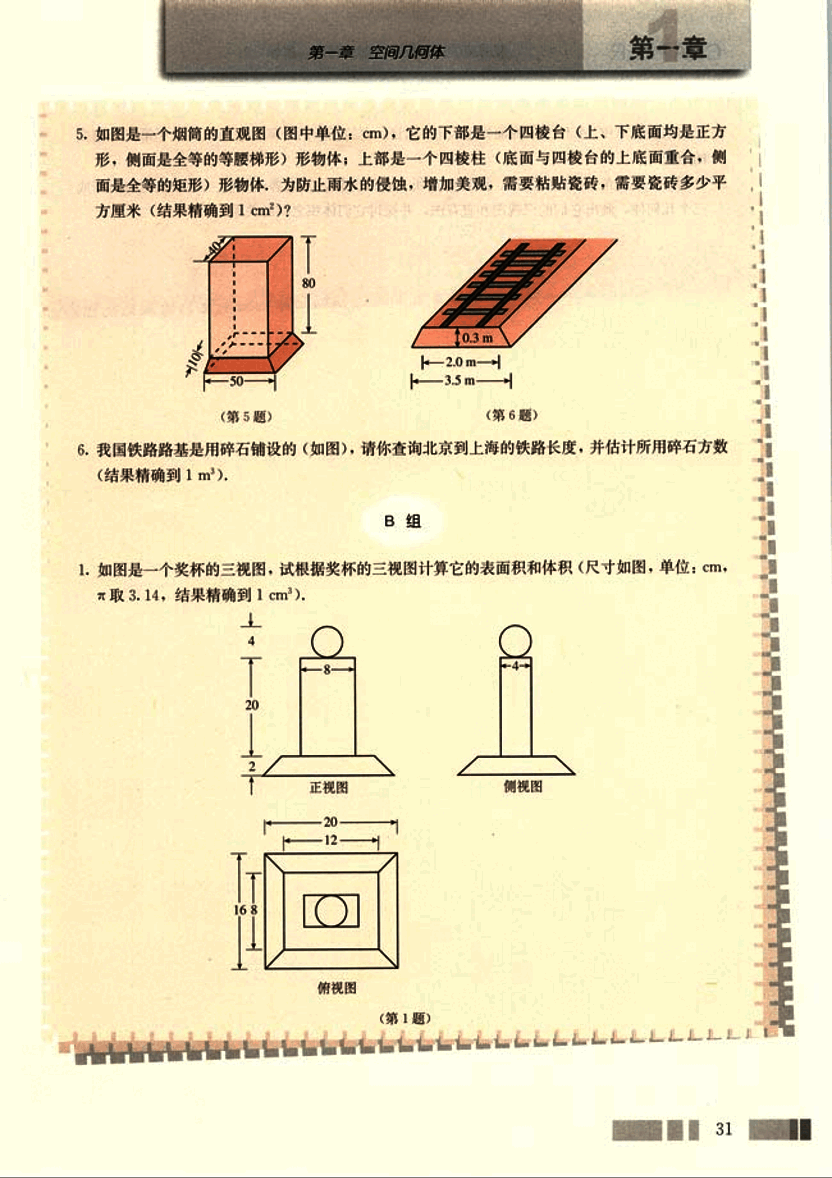
- 如图是一个烟筒的直观图(图中单位:cm),它的下部是一个四棱台(上、下底面均是正方形,侧面是全等的等腰梯形)形物体;上部是一个四棱柱(底面与四棱台的上底面重合,侧面是全等的矩形)形物体,为防止雨水的侵蚀,增加美观,需要粘贴瓷砖,需要瓷砖多少平方厘米(结果精确到1cm²)?
6.我国铁路路基是用碎石铺设的(如图),请你查询北京到上海的铁路长度,并估计所用碎石方数(结果精确到1m³).
B组
- 如图是一个奖杯的三视图,试根据奖杯的三视图计算它的表面积和体积(尺寸如图,单位:cm, π取3.14,结果精确到1cm³).
45
CHAPTER
普通高中课程标准实验教科书 数学 2
已知三棱柱 ABC-A'B'C'的侧面均是矩形,求证:它的任意两个侧面的面积和大于第三个侧面的面积。
分别以一个直角三角形的斜边、两直角边所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,画出它们的三视图和直观图,并探讨它们体积之间的关系。
32
