2.3 直线、平面垂直的判定及其性质
2.3 直线、平面垂直的判定及其性质
80
CHAPTER 2.3 直线、平面垂直的判定及其性质
图2.3-1
2.3.1 直线与平面垂直的判定
日常生活中,我们对直线与平面垂直有很多感性认识,比如,旗杆与地面的位置关系,大桥的桥柱与水面的位置关系(图2.3-1)等,都给我们以直线与平面垂直的形象。
一条直线与一个平面垂直的意义是什么?
如果一条直线垂直于一个平面内的无数条直线,那么这条直线是否与这个平面垂直?
如图2.3-2,在阳光下观察直立于地面的旗杆及它在地面的影子。随着时间的变化,尽管影子BC的位置在移动,但是旗杆AB所在直线始终与BC所在直线垂直,也就是说,旗杆AB所在直线与地面内任意一条过点B的直线垂直。事实上,旗杆AB所在直线与地面内任意一条不过点B的直线B'C'也是垂直的。
图2.3-2
如果直线 l 与平面 α 内的任意一条直线都垂直,我们就说直线 l 与平面 α 互相垂直,记作 l ⊥ α。直线 l 叫做平面 α 的垂线,平面 α 叫做直线 l 的垂面。直线与平面垂直时,它
67

81
CHAPTER 2
普通高中课程标准实验教科书 数学 2
我们唯一公共点P叫做垂足.
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的⼀边垂直,如图2.3-3.
除定义外,我们如何判断一条直线与一个平面垂直?
探究
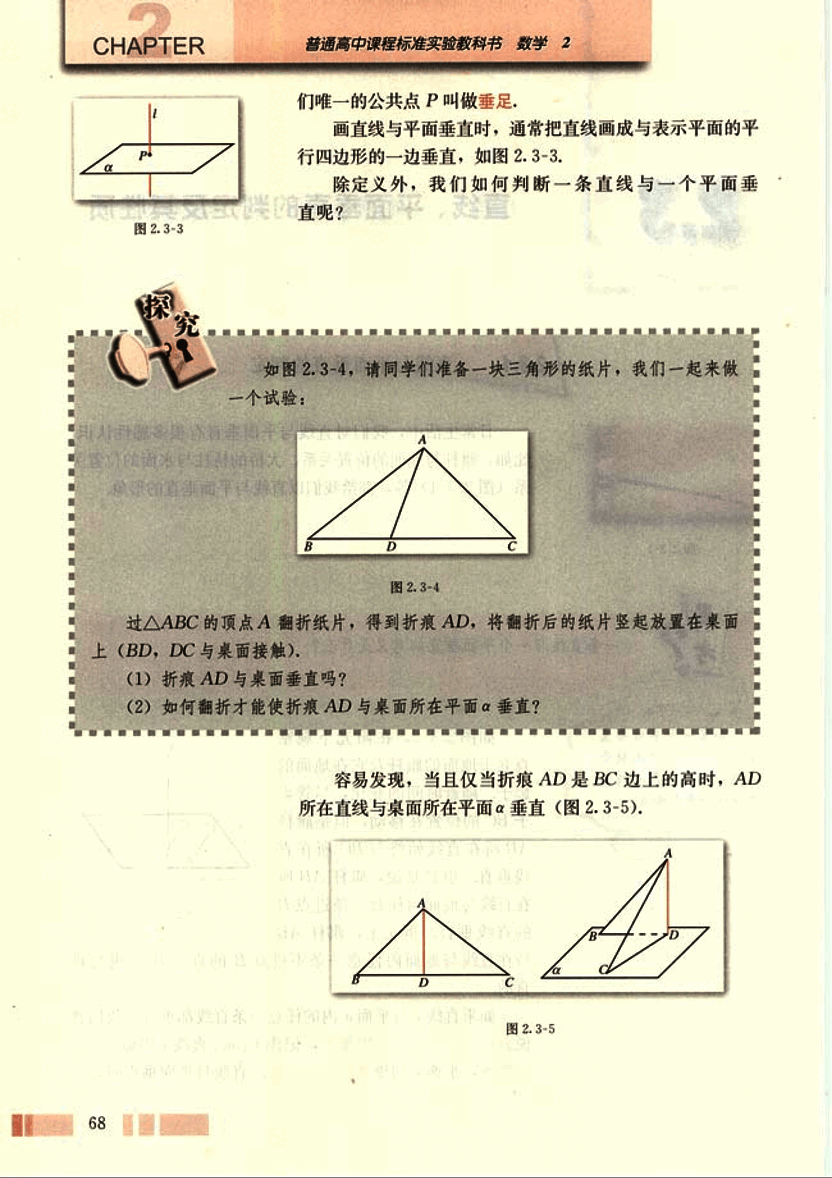
如图2.3-4,请同学们准备一块三角形的纸片,我们一起来做一个试验:
过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触)。
(1) 折痕AD与桌面垂直吗?
(2) 如何翻折才能使折痕AD与桌面所在平面垂直?
容易发现,当且仅当折痕AD是BC边上的高时,AD所在直线与桌面所在平面垂直(图2.3-5).
68
82
第二章 点、直线、平面之间的位置关系
思考
(1)有人说,折痕AD所在直线与桌面所在平面α上的一条直线垂直,就可以判断AD垂直平面α。你同意他的说法吗?
(2)如图2.3-5,由折痕AD⊥BC,翻折之后垂直关系不变,即AD⊥CD,AD⊥BD。由此你能得到什么结论?
一般地,我们有下面的判定直线与平面垂直的定理:
定理 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
定理中的“两条相交直线”这一条件不可忽视。
例1 一旗杆高8 m,在它的顶点处系两条长10 m的绳子,拉紧绳子并把它们的下端固定在地面上的两点(与旗杆脚不在同一条直线上),如果这两点与旗杆脚距6 m,那么旗杆就与地面垂直,为什么?
**解:**如图2.3-6,旗杆PO=8 m,两绳长PA=PB=10 m,OA=OB=6 m。
因为A,O,B三点不共线,
所以A,O,B三点确定平面α(即地面所在平面)。
又因为,,
所以OP⊥OA,OP⊥OB。
又因为OA∩OB=O,
所以OP⊥α。
因此,旗杆OP与地面垂直。
例2 如图2.3-7,已知a//b,a⊥a,求证b⊥a。
**证明:**在平面α内作两条相交直线m,n。
因为直线a⊥α,根据直线与平面垂直的定义知
a⊥m,a⊥n。
又因为 b//a,
所以 b⊥m,b⊥n。
又m⊂α,n⊂α,m,n是两条相交直线,
69

83
CHAPTER
普通高中课程标准实验教科书 数学 2
所以
b. a.
探究
如图 2.3-8,直四棱柱 A'B'C'D' - ABCD(侧棱与底面垂直的棱柱称为直棱柱)中,底面四边形 ABCD 满足什么条件时,A'C ⊥ BD?
练习
- 如图,在三棱锥 V-ABC 中,VA=VC,AB=BC,求证 VB⊥AC.
- 过△ABC 所在平面外一点 P,作 PO⊥α,垂足为 O,连接 PA,PB,PC.
(1) 若 PA=PB=PC,∠C=90°,则 O 是 AB 的____点.
(2) 若 PA=PB=PC,则 O 是△ABC 的____心.
(3) 若 PA⊥PB,PB⊥PC,PC⊥PA,则 O 是△ABC 的____心.
2.3.2 平面与平面垂直的判定
为了解决实际问题,人们需要研究两个平面所成的角。如图 2.3-9,修筑水坝时,为了使水坝坚固耐用,必须使水坝面与水平面成适当的角度;发射人造地球卫星时,也要根据需要,使卫星轨道平面与地球赤道平面成一定的角度,为此我们引入二面角的概念。

84
第二章 点、直线、平面之间的位置关系
(1)
(2)
平面内的一条直线把平面分成两部分,这两部分通常称为半平面。
我们常说“把门开大一些”,是指哪个角大一些?我们应该怎样刻画二面角的大小呢?
图 2.3-9
图 2.3-10
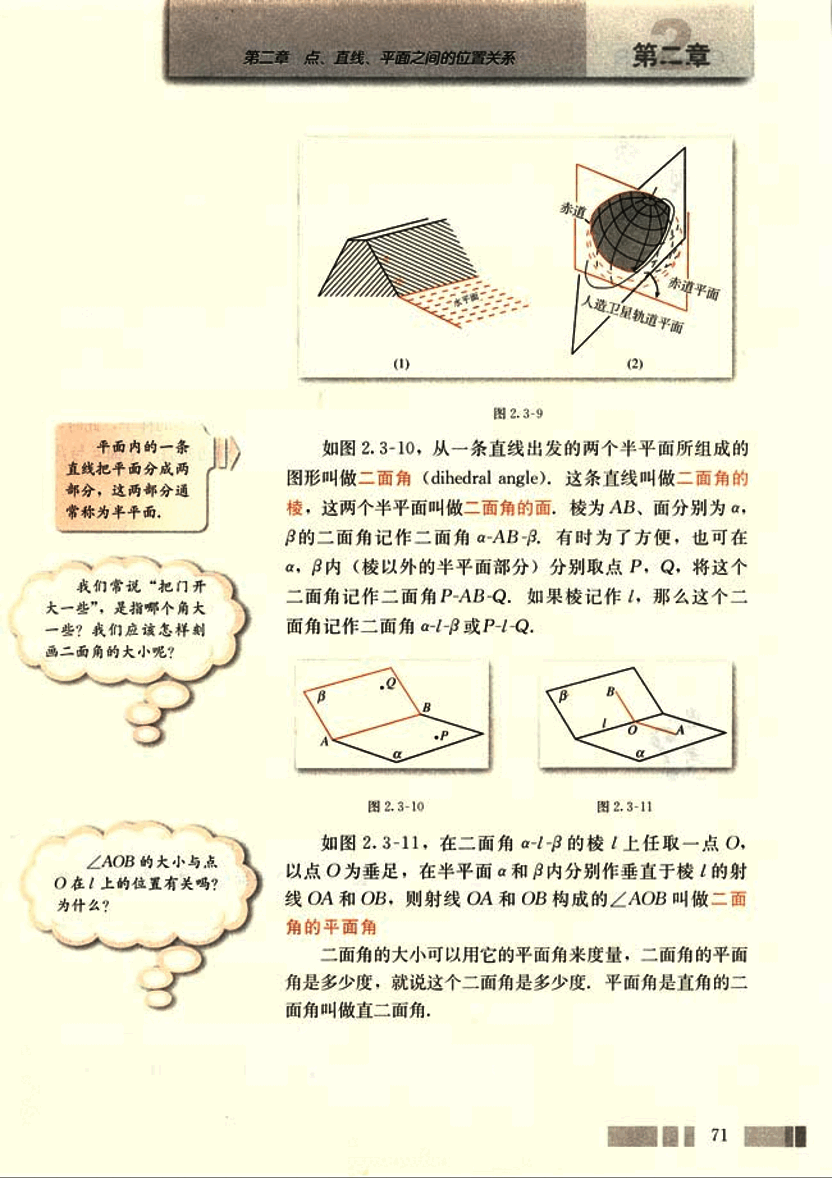
如图 2.3-10,从一条直线出发的两个半平面所组成的图形叫做二面角 (dihedral angle),这条直线叫做二面角的棱,这两个半平面叫做二面角的面。棱为 AB,面分别为 α,β 的二面角记作二面角 α-AB-β。有时为了方便,也可在 α,β 内(棱以外的半平面部分)分别取点 P,Q,将这个二面角记作二面角 P-AB-Q。如果棱记作 l,那么这个二面角记作二面角 α-l-β 或 P-l-Q。
图 2.3-10
图 2.3-11
如图 2.3-11,在二面角 α-l-β 的棱上任取一点 O,以点 O 为垂足,在半平面 α 和 β 内分别作垂直于棱的射线 OA 和 OB,则射线 OA 和 OB 构成的∠AOB 叫做二面角的平面角。
二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度。平面角是直角的二面角叫做直二面角。
71
85
CHAPTER 2
观察
教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成这些二面角的面、棱、平面角及其度数。
教室里的墙面所在平面与地面所在平面相交,它们所成的二面角是直二面角,我们常说墙面直立于地面上。
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
两个互相垂直的平面通常画成图 2.3-12 的样子,此时,把直立平面的竖边画成与水平平面的横边垂直,平面 α 与 β 垂直,记作 α⊥β。
思考
除了定义之外,如何判定两个平面互相垂直?
一般地,我们有下面判定两个平面互相垂直的定理:
定理 一个平面过另一个平面的垂线,则这两个平面垂直。
这个定理说明,可以由直线与平面垂直证明平面与平面垂直。
例 3 如图 2.3-13,AB 是⊙O 的直径,PA 垂直于⊙O 所在的平面,C 是圆周上不同于 A,B 的任意一点,求证:平面 PAC⊥平面 PBC。

86
第二章 点、直线、平面之间的位置关系
证明
设○所在平面为α,由已知条件,
PA⊥α,BC在α内,
所以PA⊥BC。
因为C是圆周上不同于A、B的任意一点,AB是○的直径,
所以∠BCA是直角,即BC⊥AC。
又因为PA与AC是△PAC所在平面内的两条相交直线,
所以,BC⊥平面PAC。
又因为BC在平面PBC内,
所以,平面PAC⊥平面PBC。
探究
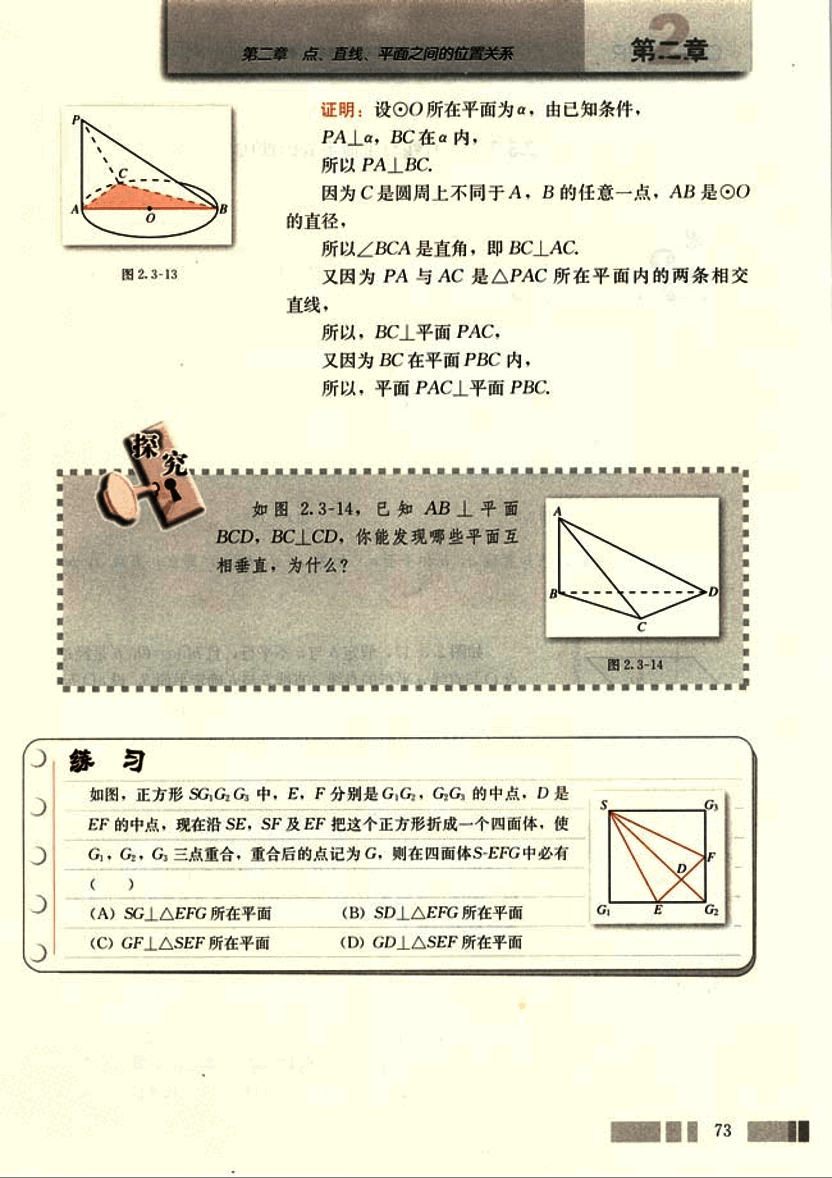
如图2.3-14,已知AB⊥平面BCD,BC⊥CD,你能发现哪些平面互相垂直,为什么?
练习
如图,正方形中,E、F分别是、的中点,D是EF的中点,现在沿SE、SF及EF把这个正方形折成一个四面体,使、、三点重合,重合后的点记为G,则在四面体S-EFG中必有( )
(A) SG⊥平面EFG
(B) SD⊥平面EFG
(C) GF⊥平面SEF
(D) GD⊥平面SEF
73
87
CHAPTER 2
2.3.3 直线与平面垂直的性质
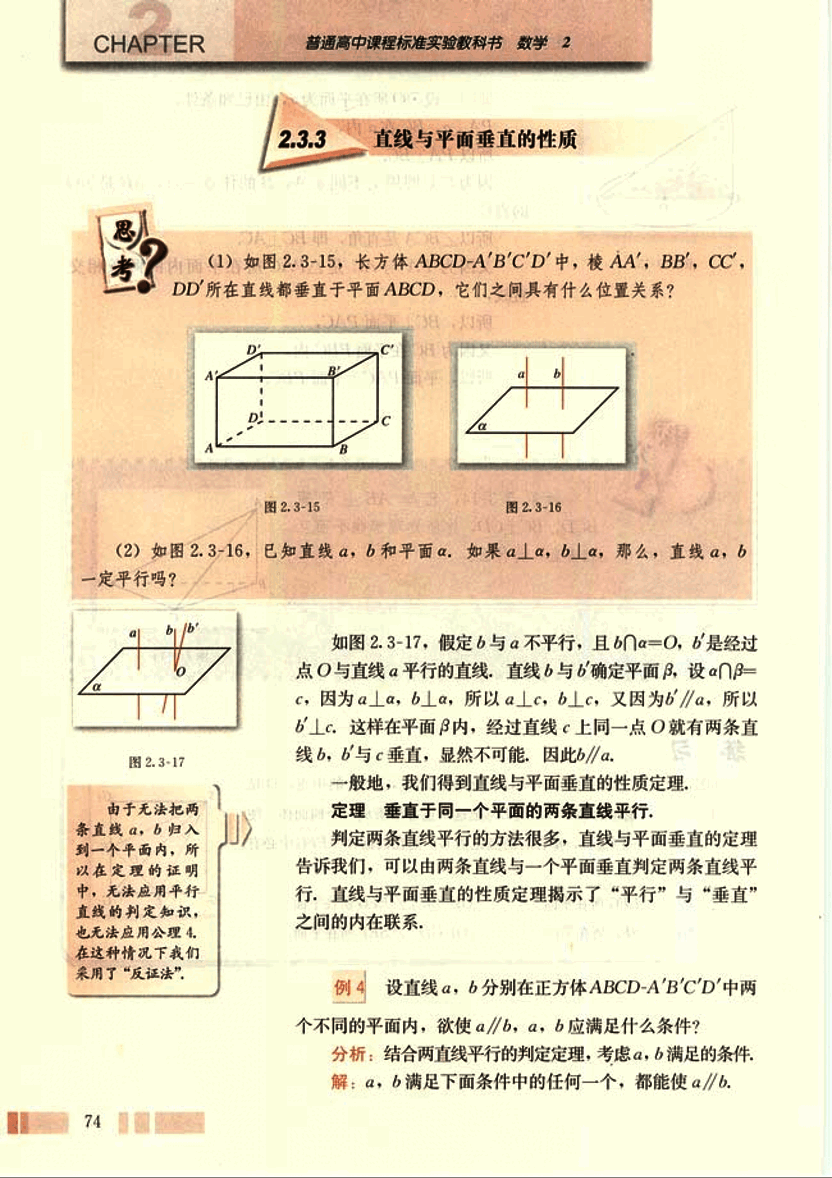
(1) 如图 2.3-15,长方体 ABCD-A'B'C'D' 中,棱 AA', BB', CC', DD' 所在直线都垂直于平面 ABCD,它们之间具有什么位置关系?
(2) 如图 2.3-16,已知直线 a, b 和平面 α。如果 α⊥a,α⊥b,那么,直线 a, b 一定平行吗?
如图 2.3-17,假定 b 与 a 不平行,且 b∩α = O,b' 是经过点 O 与直线 a 平行的直线,直线 b 与 b' 确定平面 β,设 α∩β = c', 因为 α⊥a,α⊥b,所以 α⊥c,b⊥c。又因为 b//a,所以 b'⊥c。这样在平面 β 内,经过直线上同一点就有两条直线 b, b' 与 c 垂直,显然不可能,因此 b//a。
一般地,我们得到直线与平面垂直的性质定理:
定理 垂直于同一个平面的两条直线平行。
判定两条直线平行的方法很多,直线与平面垂直的定理告诉我们,可以由两条直线与一个平面垂直判定两条直线平行,直线与平面垂直的性质定理揭示了“平行”与“垂直”之间的内在联系。
例 4 设直线 a, b 分别在正方体 ABCD-A'B'C'D' 中两个不同的平面内,欲使 a//b,a, b 应满足什么条件?
**分析:**结合两直线平行的判定定理,考虑 a, b 满足的条件。
**解:**a, b 满足下面条件中的任何一个,都能使 a//b。
88
第二章 点、直线、平面之间的位置关系
第二章
(1) a, b 同垂直于正方体的一个面;
(2) a, b 分别在正方体两个相对的面内且共面;
(3) a, b 平行于同一条棱;
(4) 如图 2.3-18,E,F,G,H 分别为 B'C',CC',AA',AD 的中点,EF 所在直线为 a,GH 所在直线为 b,等等。
思考?你还能找出其他一些条件吗?
练习
- 判断下列命题是否正确,正确的在括号内划“√”,错误的划“×”.
(1) 与同一条直线垂直的两个平面互相平行, ( )
(2) 与同一个平面垂直的两条直线互相平行, ( )
(3) 一条直线在平面内,另一条直线与这个平面垂直,则这两条直线互相垂直, ( )
- 已知直线 a,b 和平面 α,且 a⊥α,a∥b,则 b 与 α 的位置关系是 _______。
2.3.4 平面与平面垂直的性质
(1) 黑板所在平面与地面所在平面垂直,你能否在黑板上画一条直线与地面垂直?
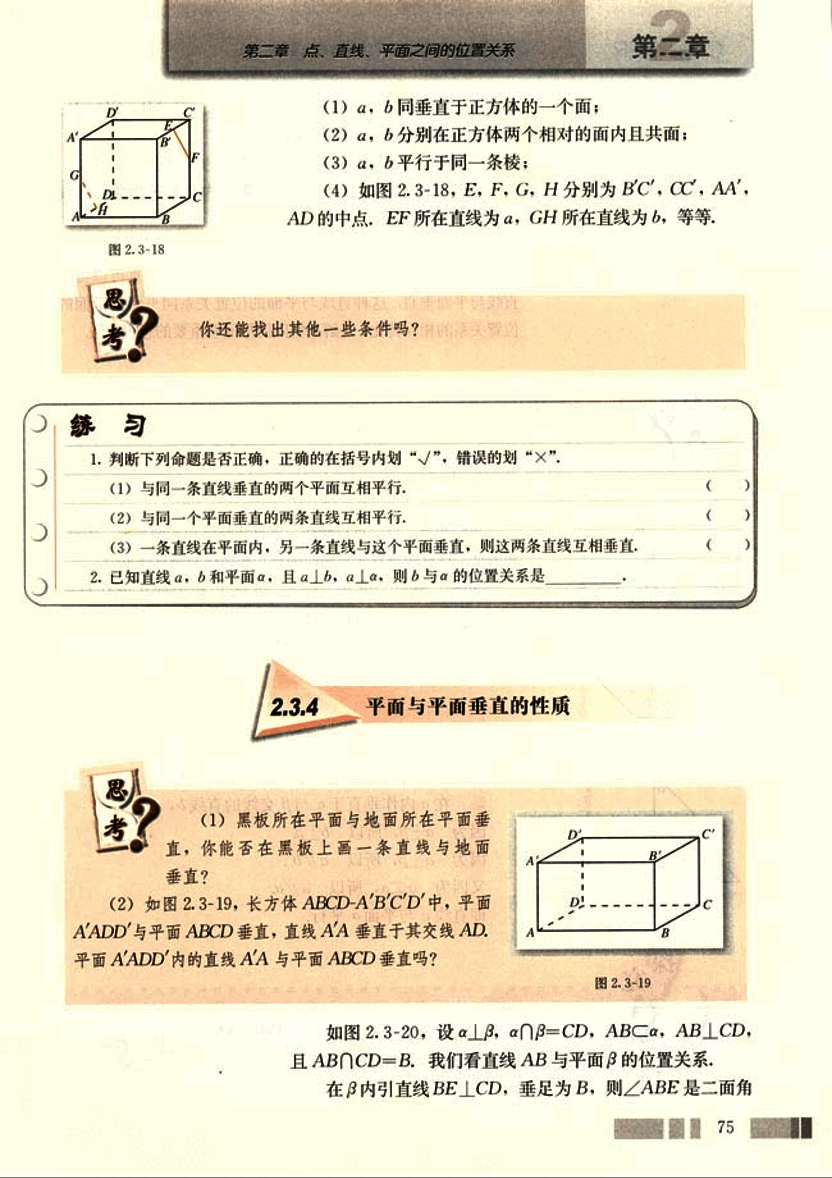
(2) 如图 2.3-19,长方体 ABCD-A'B'C'D' 中,平面 A'ADD' 与平面 ABCD 垂直,直线 A'A 垂直于其交线 AD。平面 A'ADD' 内的直线 A'A 与平面 ABCD 垂直吗?
如图 2.3-20,设 α⊥β,α∩β=CD,AB⊂α,AB⊥CD,且 AB∩CD=B。我们看直线 AB 与平面 β 的位置关系,在 β 内引直线 BE⊥CD,垂足为 B,则∠ABE 是二面角
75
89
CHAPTER
普通高中课程标准实验教科书 数学 2
α-CD-β的平面角,由α⊥β和AB⊥BE,又AB⊥CD,BE与CD是β内的两条相交直线,所以AB⊥β。
一般地,我们得到平面与平面垂直的性质定理:
定理 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
我们知道,可以通过直线与平面垂直判定平面与平面垂直;平面与平面垂直的性质定理说明,由平面与平面垂直可以得到直线与平面垂直,这种直线与平面的位置关系同平面与平面的位置关系的相互转化,是解决空间图形问题重要的思想方法。
思考?
设平面α⊥平面β,点P在平面α内,过点P作平面β的垂线α,直线α与平面α有什么位置关系?
我们知道,过一点只能作一条直线与已知平面垂直,因此,如果过一点有两条直线与平面垂直,那么这两条直线重合。
如图2.3-21,设α∩β=c,过点P在平面α内作直线b⊥c,根据平面与平面垂直的性质定理有b⊥β。
因为过一点有且只有一条直线与平面β垂直,所以直线α与直线b重合,因此α⊂α。
例5
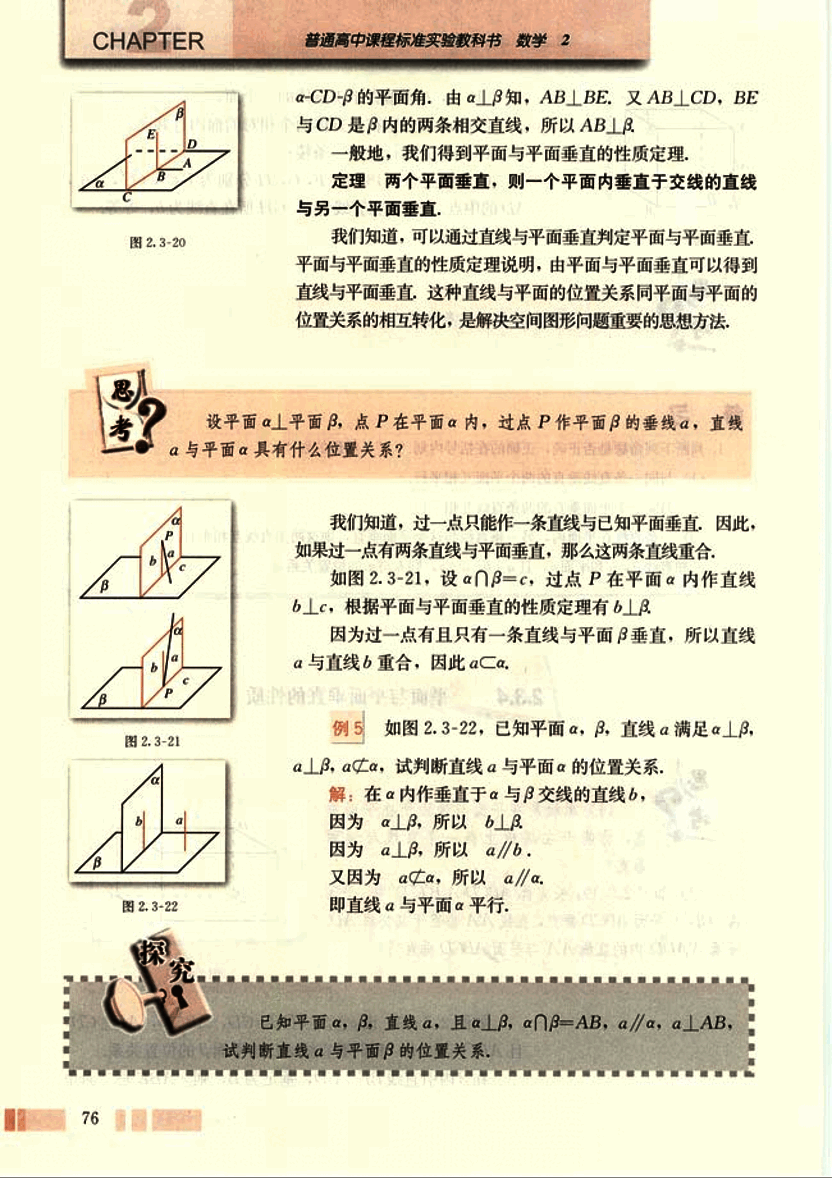
如图2.3-22,已知平面α,β,直线α满足α⊥β,α⊂α,试判断直线α与平面β的位置关系。
**解:**在α内作垂直于α与β交线的直线b。
因为α⊥β,所以b⊥β。
因为α⊂α,所以α∥b。
又因为α⊥α,所以α∥β。
即直线α与平面β平行。
已知平面α,β,直线α,且α⊥β,α∩β=AB,α∥α,α⊥AB,试判断直线α与平面β的位置关系。
76
90
第二章 点、直线、平面之间的位置关系
练习
下列命题中错误的是 ( )
(A) 如果平面 α⊥平面 β,那么平面 α 内所有直线都垂直于平面 β
(B) 如果平面 α∥平面 β,那么平面 α 内一定存在直线平行于平面 β
(C) 如果平面 α不垂直于平面 β,那么平面 α 内一定不存在直线垂直于平面 β
(D) 如果平面 α⊥平面 γ,平面 β⊥平面 γ,α∩β=l,那么 l⊥γ已知两个平面垂直,下列命题
① 一个平面内已知直线必垂直于另一个平面内的任意一条直线。
② 一个平面内的已知直线必垂直于另一个平面的无数条直线。
③ 一个平面内的任一条直线必垂直于另一个平面。
④ 过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面。
其中正确的个数是 ( )
(A) 3
(B) 2
(C) 1
(D) 0
习题 2.3
A 组
判断下列命题是否正确,正确的说明理由,错误的举例说明:
(1) 平面 α⊥平面 γ,平面 β⊥平面 γ ⇒ 平面 α⊥平面 β
(2) 平面 α∥平面 β,平面 β∥平面 γ ⇒ 平面 α∥平面 γ已知平面 α,β,γ,且 α⊥γ,β∥γ,求证 α⊥β。
如图 (第3题),在三棱锥 V-ABC 中,∠VAB=∠VAC=∠ABC=90°,试判断平面 VBA 与平面 VBC 的位置关系,并说明理由。
如图 (第4题),三棱锥 V-ABC 中,VA=VB=AC=BC=2,AB=2√3,VC=1,试画出二面角 V-AB-C 的平面角,并求它的度数。
已知平面 α,β,γ 满足 α⊥γ,β⊥γ,α∩β=l,求证:l⊥γ。
求证:如果共点的三条直线两两垂直,那么它们中每两条直线确定的平面也两两垂直。
77

91
CHAPTER 2
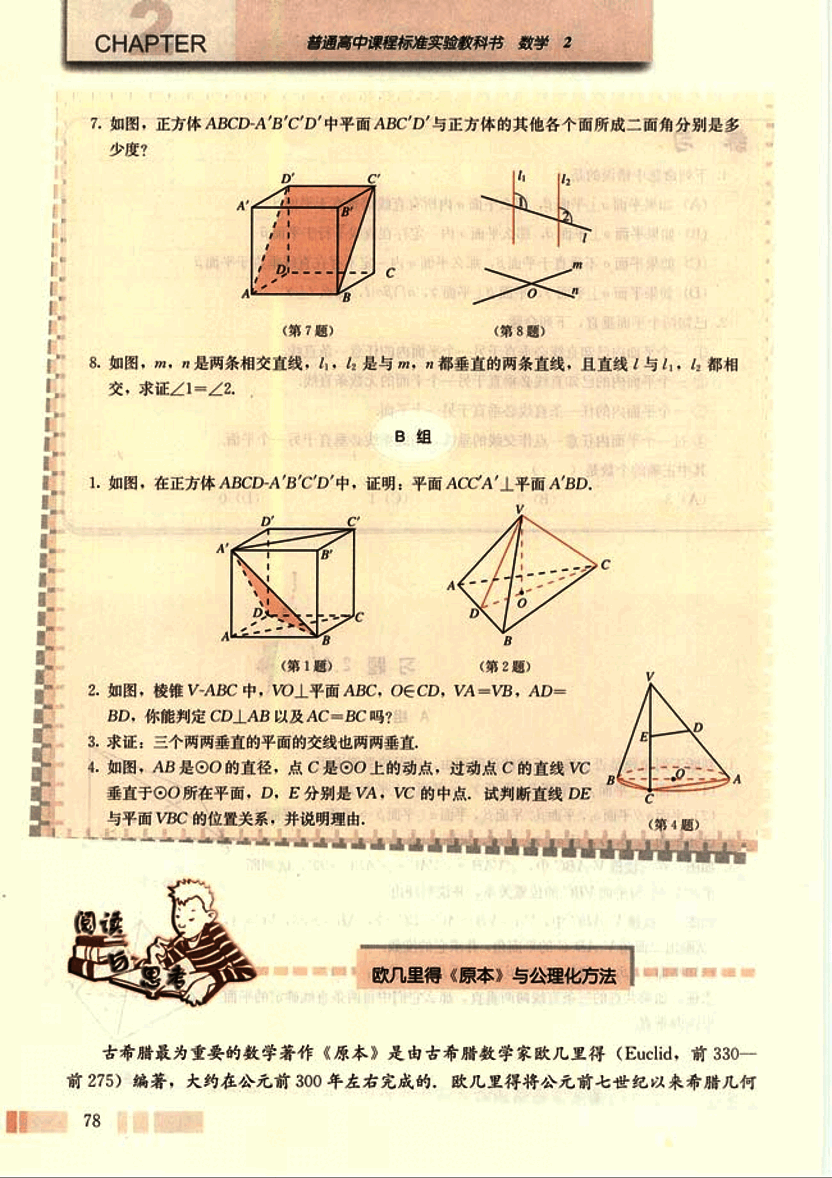
- 如图,正方体ABCD-A'B'C'D'中平面ABC'D'与正方体的其他各个面所成二面角分别是多少度?
- 如图,m, n是两条相交直线,是与m, n都垂直的两条直线,且直线l与都相交,求证。
- 如图,在正方体ABCD-A'B'C'D'中,证明:平面ACCA'⊥平面A'BD.
- 如图,棱锥V-ABC中,VO⊥平面ABC,OE⊥CD,VA=VB,AD=BD,你能判定CD∥AB以及AC=BC吗?
求证:三个两两垂直的平面的交线也两两垂直。
如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在平面,D,E分别是VA,VC的中点,试判断直线DE与平面VBC的位置关系,并说明理由。
欧几里得《原本》与公理化方法
古希腊最为重要的数学著作《原本》是由古希腊数学家欧几里得(Euclid, 前330—前275)编著,大约在公元前300年左右完成的,欧几里得将公元前七世纪以来希腊几何
78
92
第二章 点、直线、平面之间的位置关系
第二章
学家积累起来的丰富成果整理、收集起来,并且加以系统化,
他从少数已被经验反复验证的公理出发,运用逻辑推理以及数
学运算方法演绎出一系列定理与推论,写成了十三卷在数学发
展史上具有极其深远影响的数学巨著《原本》,使几何学成为
一门独立的、演绎的科学。
欧几里得《原本》是一部划时代的著作,其伟大的历史意
义是它在人类数学史中第一次给出了公理化的数学体系,过去
所积累下来的数学知识,是零碎的、片断的,欧几里得借助逻
辑方法,把这些知识组织起来,加以分类、比较,揭示彼此间
的内在联系,整理在一个严密的系统之中。《原本》体现了这
种理性精神,它对整个数学的发展产生深远的影响,正因为如此,《原本》得以跨越地域、
民族、语言、时间的一切障碍传播到了整个世界,公理化方法作为一种理论形式为人们普
遍接受,人们现在已普遍建立了这样的认识,所有的数学理论,都必须按照数学的定义、
公理与三段论的逻辑论证来组织。《原本》为数学发展树起一面旗帜,并成为理性思维的
象征。
什么是公理化方法呢?
数学公理化方法,就是从尽可能少的原始概念(基本概念)和尽可能少的一组不加证
明的原始命题(公理、公设)出发,应用严格的逻辑推理,推导出其余的命题,使某一数
学分支成为演绎系统的一种方法。
基本概念是一些不加定义的原始概念,它们必须是真正基本的,无法用更原始、更基
本的概念去定义的,如中学数学中的点、直线、平面、集合等概念都是基本概念。
公理是对基本概念间的相互关系和基本性质所作的一种阐述和规定,如“过两点至少
有一条直线”“经过不在同一条直线上的三点,有且只有一个平面”等都是作为公理的
命题。
公理化方法主要有以下三个作用:
① 概括整理数学知识,《原本》就是欧几里得用公理化的方法把零散的几何知识归为
一体,树立了以公理化方法研究数学的典范。
② 促进新理论的创立,由于公理化方法把数学分支的基础分析得十分清楚,结构严
谨有序,这就有利于比较数学各分支实质上的异同,从而推动和促进数学新理论的产生,
促进数学基础的研究与探索,例如,非欧几何就是在研究和应用公理化的过程中产
生的。
③ 对其他学科有示范作用,由于数学公理化方法表述数学理论的简捷性、条理性、
以及结构的和谐性,为其他科学理论的表述起了示范作用,其他科学纷纷效法,建立了自
己的公理化系统。
79
