3.1 直线的倾斜角与斜率
3.1 直线的倾斜角与斜率
99
CHAPTER 3
3.1 直线的倾斜角与斜率
在平面直角坐标系中,点用坐标表示,直线如何表示呢?为了用代数方法研究直线的有关问题,本节首先探索确定直线位置的几何要素,然后在坐标系中用代数方法把这些几何要素表示出来。
3.1.1 倾斜角与斜率
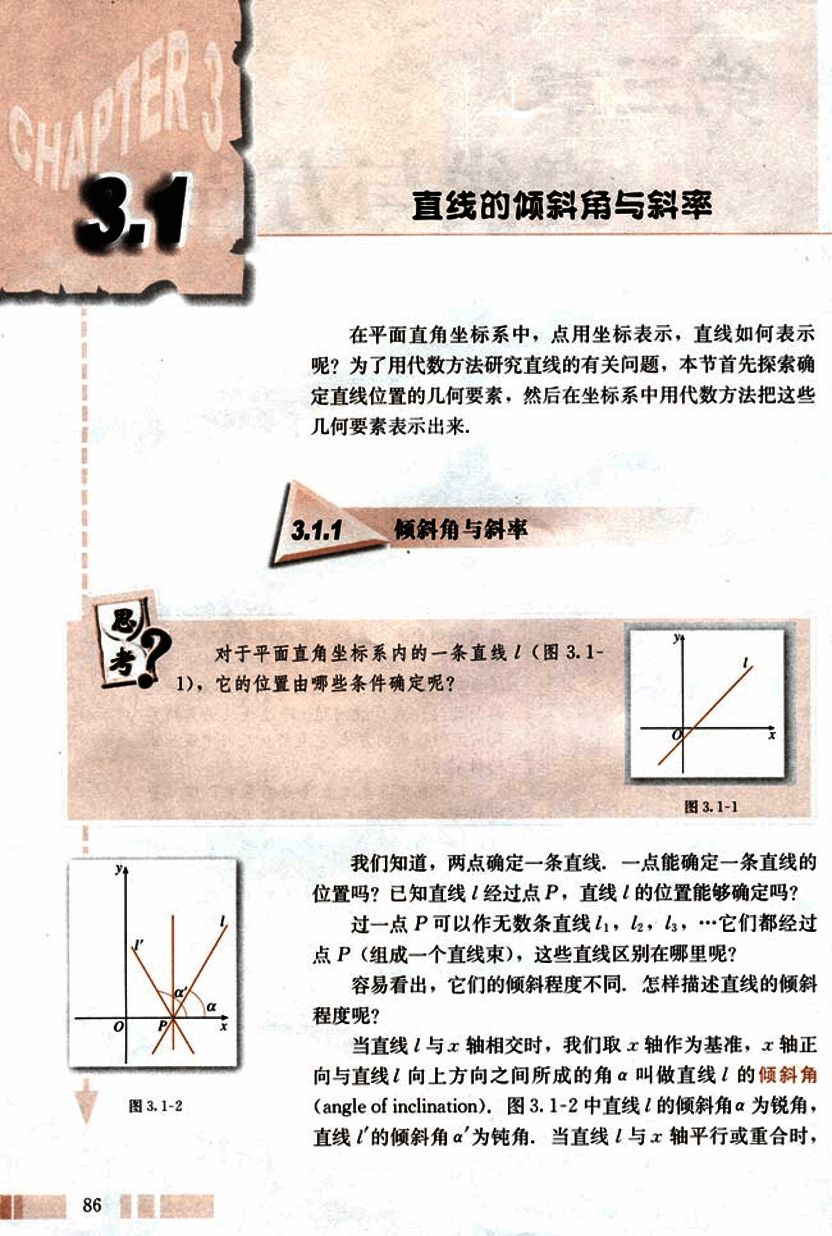
对于平面直角坐标系内的一条直线(图 3.1-1),它的位置由哪些条件确定呢?
我们知道,两点确定一条直线,一点能确定一条直线的位置吗?已知直线经过点 P,直线的位置能够确定吗?
过一点 P 可以作无数条直线,……它们都经过点 P(组成一个直线束),这些直线区别在哪里呢?
容易看出,它们的倾斜程度不同,怎样描述直线的倾斜程度呢?
当直线与 x 轴相交时,我们取 x 轴作为基准,x 轴正向与直线向上方向之间所成的角叫做直线的倾斜角(angle of inclination)。图 3.1-2 中直线的倾斜角为锐角,直线的倾斜角为钝角。当直线与 x 轴平行或重合时,
100
第三章 直线与方程
我们规定它的倾斜角为 0°。因此,直线的倾斜角 α 的取值范围为
0°<α<180°。
这样,平面直角坐标系内每一条直线都有一个确定的倾斜角 α,且倾斜程度相同的直线,其倾斜角相等;倾斜程度不同的直线,其倾斜角不相等。因此,我们可用倾斜角 α 表示平面直角坐标系内一条直线的倾斜程度。
如上所述,在平面直角坐标系中,已知直线上的一个点不能确定一条直线的位置,同样,已知直线的倾斜角 α,也不能确定一条直线的位置。但是,直线上的一点和这条直线的倾斜角可以唯一确定一条直线。因此,确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角,二者缺一不可。
思考
日常生活中,还有没有表示倾斜程度的量?
如图 3.1-3,日常生活中,我们经常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),即
坡度(比)=
例如,“进 2 升 3”与“进 2 升 2”比较,前者更陡一些,因为坡度(比) > 。
如果我们使用“倾斜角”这个概念,那么这里的“坡度(比)”实际就是“倾斜角的正切”。我们把一条直线的倾斜角的正切值叫做这条直线的斜率(slope)。斜率常用小写字母 k 表示,即
。
例如,倾斜角 α=45° 时,这条直线的斜率
;
倾斜角 α=135° 时,由,得
,
即这条直线的斜率为-1。
87

101
CHAPTER 3
普通高中课程标准实验教科书 数学 2
倾斜角不是 90° 的直线都有斜率,而且倾斜角不同,直线的斜率也不同。因此,我们可以用斜率表示直线的倾斜程度。
下面我们探究如何由直线上两点的坐标计算直线的斜率。
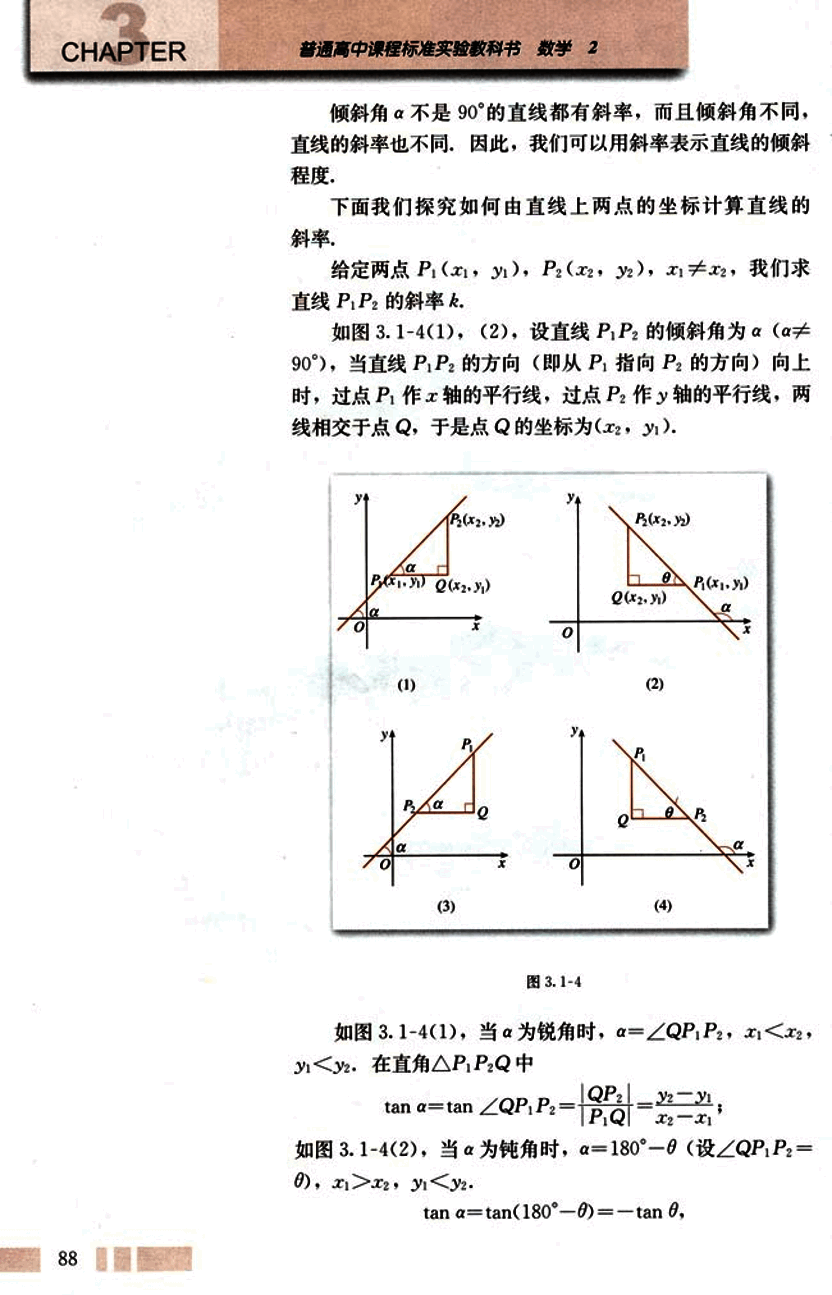
给定两点,,,我们求直线的斜率。
如图 3.1-4(1),(2),设直线的倾斜角为(),当直线的方向(即从指向的方向)向上时,过点作轴的平行线,过点作轴的平行线,两线相交于点,于是点的坐标为。
图 3.1-4
如图 3.1-4(1), 当为锐角时, , , 。在直角中
;
如图 3.1-4(2), 当为钝角时, (设), , 。
,
102
第三章 直线与方程
在直角 △P₁P₂Q 中
tan θ =
于是可得
tan α =
即
k =
同样,当 P₂P₁ 的方向向上时,如图 3.1-4(3),(4),也有
tan α =
即
k =
当直线 P₁P₂ 与 x 轴平行或重合时,上述式子还成立吗?为什么?
综上所述,我们得到经过两点 P₁(x₁,y₁), P₂(x₂, y₂)(x₁≠x₂)的直线的斜率公式
k =
已知直线上两点 A(a₁,a₂), B(b₁, b₂),运用上述公式计算直线 AB 斜率时,与 A,B 两点坐标的顺序有关吗?
当直线平行于 y 轴,或与 y 轴重合时,上述公式还适用吗?为什么?
例 1
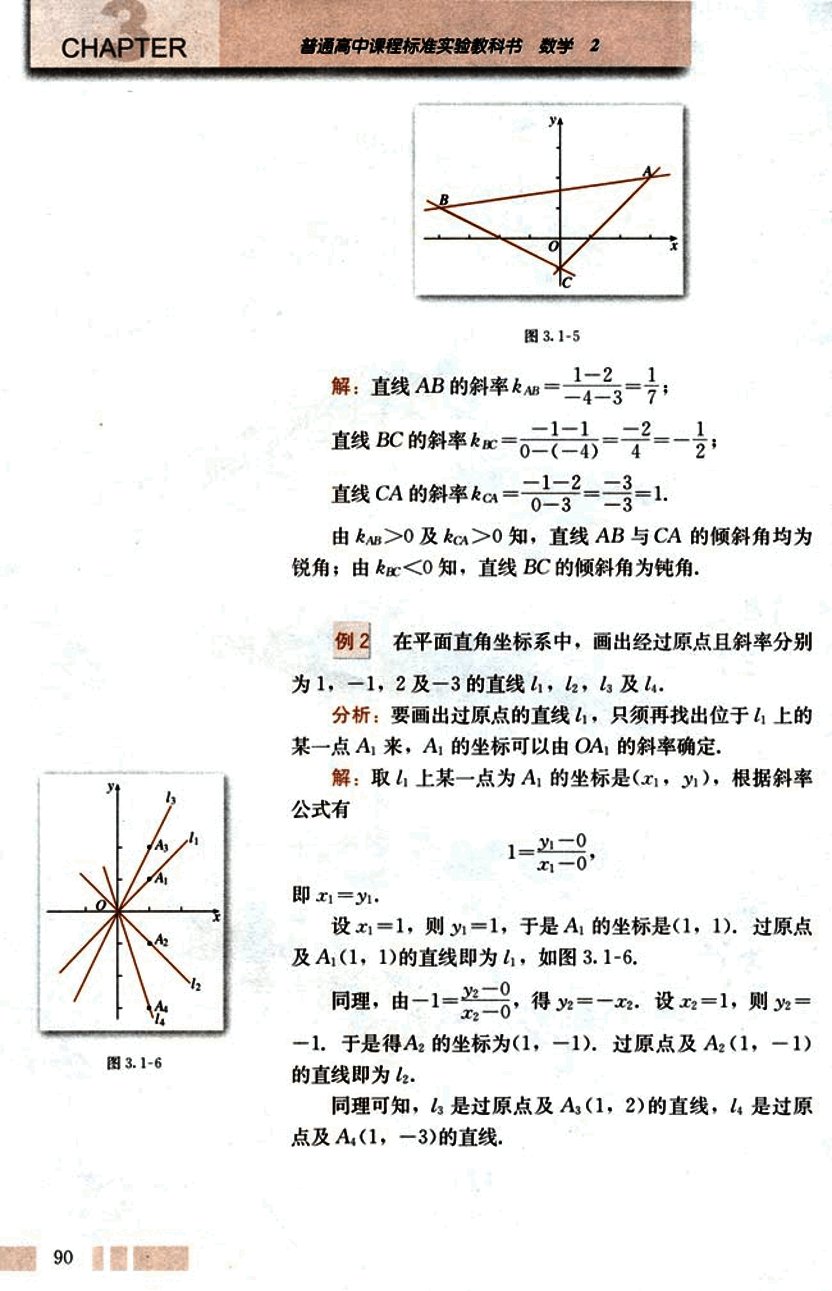
如图 3.1-5,已知 A(3, 2), B(-4, 1), C(0, -1),求直线 AB, BC, CA 的斜率,并判断这些直线的倾斜角是锐角还是钝角。
89

103
CHAPTER 3
图 3.1-5
解: 直线 AB 的斜率 ;
直线 BC 的斜率 ;
直线 CA 的斜率 .
由 及 知,直线 AB 与 CA 的倾斜角均为锐角;由 知,直线 BC 的倾斜角为钝角。
例 2
在平面直角坐标系中,画出经过原点且斜率分别为 1,-1,2 及 -3 的直线 ,, 及 。
分析: 要画出过原点的直线 ,只须再找出位于 上的某一点 来, 的坐标可以由 的斜率确定。
解: 取 上某一点为 的坐标是 ,根据斜率公式有
,
即 .
设 ,则 ,于是 的坐标是 (1, 1)。过原点及 (1, 1) 的直线即为 ,如图 3.1-6。
同理,由 得 。设 ,则 。于是得 的坐标为 (1, -1)。过原点及 (1, -1) 的直线即为 。
同理可知, 是过原点及 (1, 2) 的直线, 是过原点及 (1, -3) 的直线。
104
第三章 直线与方程
练习
已知下列直线的倾斜角,求直线的斜率:
(1) ;
(2) ;
(3) ;
(4) .求经过下列两点直线的斜率,并判断其倾斜角是锐角还是钝角:
(1) C(18, 8), D(4, -4);
(2) P(0, 0), Q(-1, ).已知 a, b, c 是两两不等的实数,求经过下列两点直线的倾斜角:
(1) A(a, c), B(b, c);
(2) C(a, b), D(a, c);
(3) P(b, b+c), Q(a, c+a).画出经过点(0, 2), 且斜率分别为 2 与-2 的直线.
3.1.2 两条直线平行与垂直的判定
为了在平面直角坐标系内表示直线的倾斜程度,我们引入了直线倾斜角的概念,进而又引入了直线的斜率——表示直线相对于 x 轴的倾斜程度,并导出了计算斜率的公式,即把几何问题转化为代数问题,那么,我们能否通过直线的斜率,来判断两条直线的位置关系呢?
设两条直线, 的斜率分别为, .
时,与满足什么关系?
若,则与的倾斜角与相等,如图 3.1-7. 由,可得,即。因此
若,则.
反之,若,则.
于是我们得到,对于两条不重合的直线, ,其斜率分别为, ,有
.
91

105
CHAPTER 3
例 3
已知 A (2, 3), B(-4, 0), P(-3, 1), Q(-1, 2), 试判断直线 BA 与 PQ 的位置关系,并证明你的结论。
解:如图 3.1-8,
直线 BA 的斜率
直线 PQ 的斜率
因为 ,所以直线 BA // PQ。
例 4
已知四边形 ABCD 的四个顶点分别为 A(0, 0), B(2, -1), C(4, 2), D(2, 3), 试判断四边形 ABCD 的形状,并给出证明。
解:如图 3.1-9,
AB 边所在直线的斜率
CD 边所在直线的斜率
BC 边所在直线的斜率
DA 边所在直线的斜率
因为 ,,所以 AB // CD, BC // DA。
因此四边形 ABCD 是平行四边形。
思考
时, 与 满足什么关系?
设两条直线 与 的倾斜角分别为 与 (, )。
如图 3.1-10,如果 ,这时 (为什么?),由三角形任一外角等于其不相邻两内角之和,即
因为 的斜率分别为 ,且 (为什么?),
92
106
第三章 直线与方程
由
得
当 时, 与 的位置关系如何?
由上我们得到,如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;反之,如果它们的斜率之积等于-1,那么它们互相垂直,即
例 5 已知 A(-6, 0), B(3, 6), P(0, 3), Q(6, 6), 试判断直线 AB 与 PQ 的位置关系。
解:直线 AB 的斜率
直线 PQ 的斜率
由于
所以直线 AB ⊥ PQ.
例 6 已知 A(5, -1), B(1, 1), C(2, 3) 三点,试判断 △ABC 的形状。
分析:如图 3.1-11,猜想 AB ⊥ BC,△ABC 是直角三角形。
解:AB 边所在直线的斜率
BC 边所在直线的斜率
93

107
CHAPTER
普通高中课程标准实验教科书 数学 2
由,得,即。
所以是直角三角形。
练习
判断下列各对直线平行还是垂直:
(1) 经过两点 A(2, 3), B(-1, 0)的直线,与经过点 P(1, 0)且斜率为 1 的直线;
(2) 经过两点 C(3, 1), D(-2, 0)的直线,与经过点 M(1, -4)且斜率为-5 的直线。试确定 m 的值,使过点 A(m, 1), B(-1, m)的直线与过点 P(1, 2), Q(-5, 0)的直线
(1) 平行; (2) 垂直。
习题 3.1
A 组
已知直线斜率的绝对值等于 1,求直线的倾斜角。
已知四边形 ABCD 的四个顶点是 A(2, 3), B(1, -1), C(-1, -2), D(-2, 2), 求四边形 ABCD 的四条边所在直线的斜率。
已知直线的斜率 k = 2, A(3, 5), B(x, 7), C(-1, y)是这条直线上的三个点,求 x 和 y 的值。
(1) m 为何值时,经过两点 A(-m, 6), B(1, 3m)的直线的斜率是 12?
(2) m 为何值时,经过两点 A(m, 2), B(-m, -2m - 1)的直线的倾斜角是 60°?已知 A(1, 2), B(-1, 0), C(3, 4)三点,这三点是否在同一条直线上,为什么?
判断下列各小题中的直线与是否平行:
(1) 的斜率为 2,经过点 A(1, 2), B(4, 8);
(2) 经过点 P(3, 3), Q(-5, 3),平行于 x 轴,但不经过 P,Q 两点;
(3) 经过点 M(-1, 0), N(-5, -2),经过点 R(-4, 3), S(0, 5)。判断下列各小题中的每对直线是否垂直:
(1) 的斜率为,经过点 A(1, 1), B(0, );
(2) 的倾斜角为 45°,经过点 P(-2, -1), Q(3, -6)。
94

108
第三章 直线与方程
(3) 4 经过点 M(1, 0), N(4, -5), 4 经过点 R(-6, 0), S(-1, 3).
- 已知 A(1, -1), B(2, 2), C(3, 0) 三点, 求点 D, 使直线 CD⊥AB, 且 CB//AD.
B 组
已知点 M(2, 2) 和 N(5, -2), 点 P 在 x 轴上, 且 ∠MPN 为直角, 求点 P 的坐标.
4 经过点 A(m, 1), B(-3, 4), 4 经过点 C(1, m), D(-1, m+1), 当直线 4 与 4 平行或垂直时, 求 m 的值.
已知四边形 ABCD 的顶点为 A(2, 2+2√2), B(-2, 2), C(0, 2-2√2), D(4, 2), 求证四边形 ABCD 为矩形.
已知四边形 ABCD 的顶点为 A(m, n), B(6, 1), C(3, 3), D(2, 5), 求 m 和 n 的值, 使四边形 ABCD 为直角梯形.
过两点 A(m²+2, m²-3), B(3-m-m², 2m) 的直线的倾斜角为 45°, 求 m 的值.
经过点 P(0, -1) 作直线 4, 若直线 4 与连接 A(1, -2), B(2, 1) 的线段总有公共点, 借助信息技术工具, 找出直线 4 的倾斜角 α 与斜率 k 的取值范围, 并说明理由.
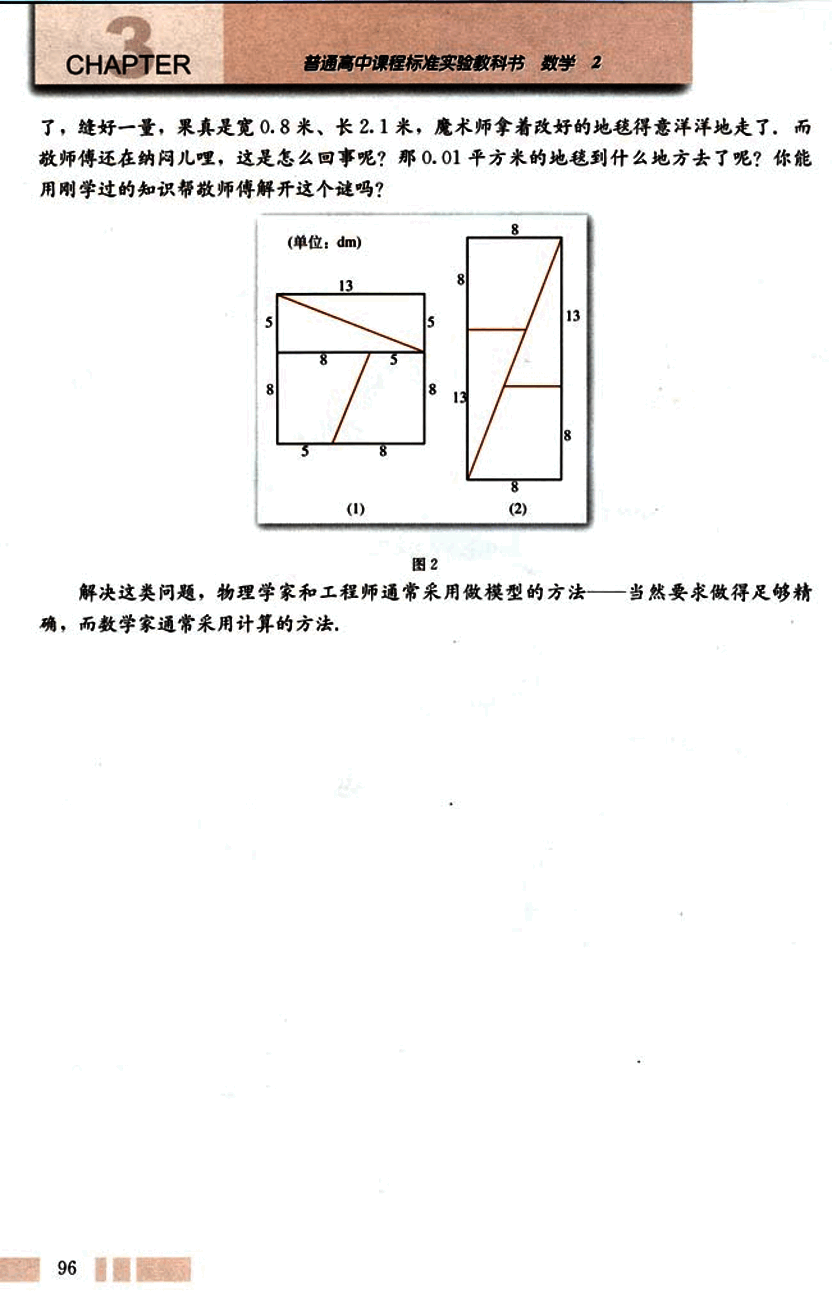
魔术师的地毯
一天, 著名魔术大师秋先生拿了一块长和宽都是 1.3 米的地毯去找地毯匠敬师傅 (图 1), 要求把这块正方形的地毯改制成宽 0.8 米, 长 2.1 米的矩形, 敬师傅对秋先生说: “你这位鼎鼎大名的魔术师, 难道连小学算术都没有学过吗? 边长为 1.3 米的正方形面积为 1.69 平方米, 而宽 0.8 米, 长 2.1 米的矩形面积只有 1.68 平方米, 两者并不相等啊! 除非裁去 0.01 平方米, 不然没法做.” 秋先生拿出他事先画好的两张设计图, 对敬师傅说: “你先照这张图 (图 2(1)) 的尺寸把地毯裁成四块, 然后再照另一张图 (图 2(2)) 的样子把这四块拼在一起缝好就行了, 魔术大师是从来不会出错的, 你只管放心做吧!” 敬师傅照着做 图 1 95

109
CHAPTER 3
普通高中课程标准实验教科书 数学 2
- 缝好一量,果真是宽 0.8 米,长 2.1 米,魔术师拿着改好的地毯得意洋洋地走了。而敬师傅还在纳闷儿哩,这是怎么回事呢?那 0.01 平方米的地毯到什么地方去了呢?你能用刚学过的知识帮敬师傅解开这个谜吗?
(单位: dm)
| 8 | 8 | |
| 13 | ||
| 5 | 5 | |
| 8 | ||
| 8 | 8 | |
| 5 | ||
| 5 | 5 | |
| (1) | (2) |
图 2
解决这类问题,物理学家和工程师通常采用做模型的方法——当然要求做得足够精确,而数学家通常采用计算的方法。
96