4.1 圆的方程
4.1 圆的方程
137
CHAPTER 4
4.1 圆的方程
4.1.1 圆的标准方程
我们知道,在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线。
思考?在平面直角坐标系中,如何确定一个圆呢?
显然,当圆心位置与半径大小确定后,圆就唯一确定了。因此,确定一个圆最基本要素是圆心和半径。如图 4.1-1,在直角坐标系中,圆心(点)A 的位置用坐标(a, b)表示,半径 r 的大小等于圆上任意点 M(x, y)与圆心 A(a, b)的距离,圆心为 A 的圆就是集合
P =
由两点间的距离公式,点 M 的坐标适合的条件可以表示为
①
① 式两边平方,得
(1)
若点 M(x, y)在圆上,由上述讨论可知,点 M 的坐标适合方程(1);反之,若点 M(x, y)的坐标适合方程(1),这就说明点 M 与圆心 A 的距离为 r,即点 M 在圆心为 A 的圆上。我们把方程(1)称为圆心为 A(a, b),半径长为 r

138
第四章 圆与方程
圆心在坐标原点,半径长为 r 的圆的方程是什么?
的圆的方程,把它叫做圆的标准方程 (standard equation of circle).
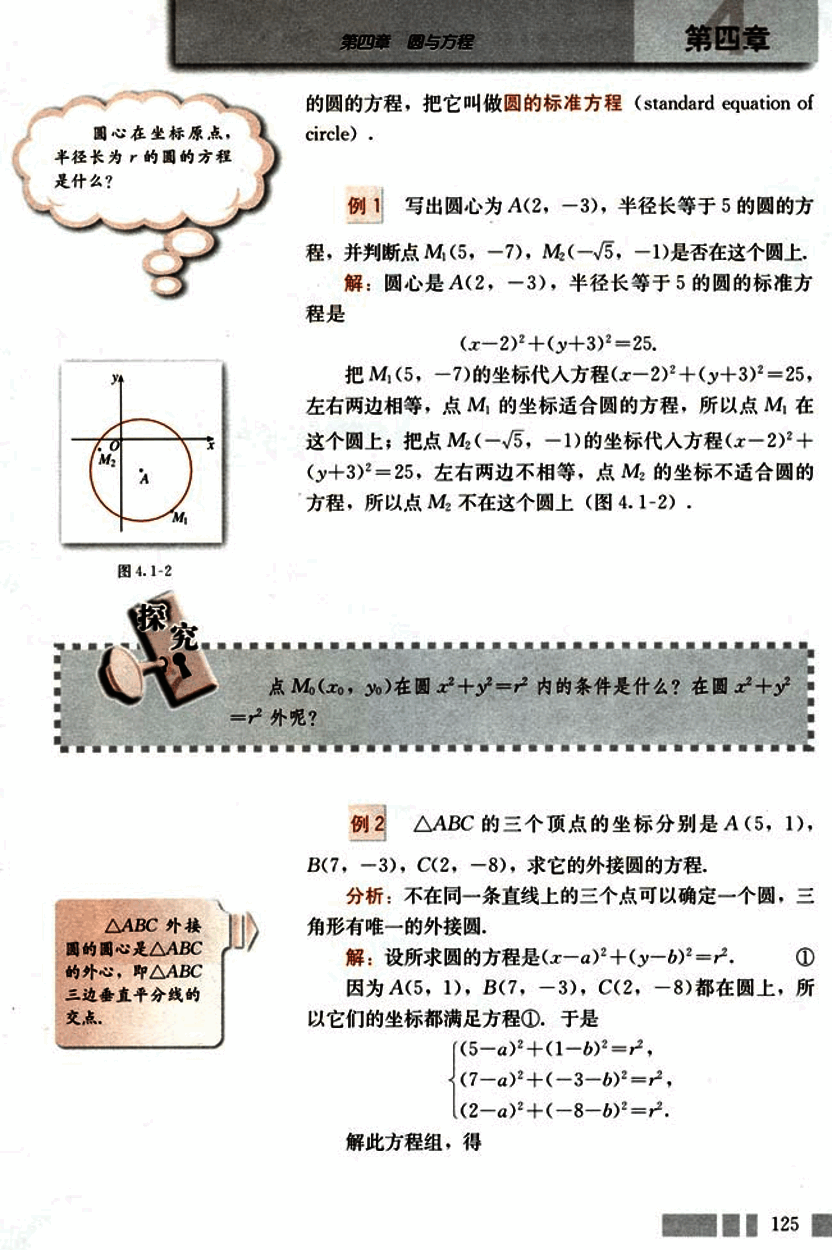
例 1
写出圆心为 A(2, -3),半径长等于 5 的圆的方程,并判断点 M₁(5, 7), M₂(-√5, -1) 是否在这个圆上。
解:圆心是 A(2, -3),半径长等于 5 的圆的标准方程是
(x - 2)² + (y + 3)² = 25.
把 M₁(5, 7) 的坐标代入方程 (x - 2)² + (y + 3)² = 25,左右两边相等,点 M₁ 的坐标适合圆的方程,所以点 M₁ 在这个圆上;把点 M₂(-√5, -1) 的坐标代入方程 (x - 2)² + (y + 3)² = 25,左右两边不相等,点 M₂ 的坐标不适合圆的方程,所以点 M₂ 不在这个圆上 (图 4.1-2)。
探究
点 M₀(x₀, y₀) 在圆 x² + y² = r² 内的条件是什么?在圆 x² + y² = r² 外呢?
例 2
△ABC 的三个顶点的坐标分别是 A(5, 1), B(7, -3), C(2, -8), 求它的外接圆的方程。
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆。
解:设所求圆的方程是 (x - a)² + (y - b)² = r². ①
因为 A(5, 1), B(7, -3), C(2, -8) 都在圆上,所以它们的坐标都满足方程 ①,于是
(5 - a)² + (1 - b)² = r²
(7 - a)² + (-3 - b)² = r²
(2 - a)² + (-8 - b)² = r²解此方程组,得…
125
139
CHAPTER
普通高中课程标准实验教科书 数学 2
所以,△ABC 的外接圆的方程是
(x-2)²+(y+3)²=25.
例 3
已知圆心为 C 的圆经过点 A(1,1)和 B(2,-2),且圆心 C 在直线 l: x-y+1=0 上,求圆心为 C 的圆的标准方程.
分析: 如图 4.1-3,确定一个圆只需确定圆心位置与半径大小,圆心为 C 的圆经过点 A(1,1)和 B(2,-2),由于圆心 C 与 A,B 两点的距离相等,所以圆心 C 在线段 AB 的垂直平分线上,又圆心 C 在直线 l 上,因此圆心 C 是直线 l 与直线的交点,半径长等于|CA|或|CB|.
解: 因为 A(1, 1),B(2,-2),所以线段 AB 的中点 D 的坐标为(,),直线 AB 的斜率
.
因此线段 AB 的垂直平分线的方程是
.
即 x-3y-3=0.
圆心 C 的坐标是方程组
的解.
解此方程组,得
所以圆心 C 的坐标是(-3,-2).
圆心为 C 的圆的半径长
.
所以,圆心为 C 的圆的标准方程是
(x+3)²+(y+2)²=25.
126
比较例 2 和例 3,你能归纳求任意 △ABC 外接圆的方程的两种方法吗?

140
第四章 圆与方程
练习
写出下列圆的标准方程:
(1) 圆心在 C(-3, 4), 半径长是;
(2) 圆心在 C(8, -3), 且经过点 M(5, 1).已知圆的方程是,利用计算器,判断下列各点在圆上、在圆外、还是在圆内?
(1) ;
(2) ;
(3) .已知两点,,求以线段为直径的圆的方程,并判断点 M(6, 9), N(3, 3), Q(5, 3)在圆上、在圆内、还是在圆外(可利用计算器)?
已知的顶点坐标分别是 A(4, 0), B(0, 3), O(0, 0), 求外接圆的方程.
4.1.2 圆的一般方程
方程表示什么图形?方程表示什么图形?
对方程配方,可得
.
此方程表示以(1, -2)为圆心,2 为半径长的圆.
同样,对方程配方,得,由于不存在点的坐标(x, y)满足这个方程,所以这个方程不表示任何图形.
方程在什么条件下表示圆?
我们来研究方程
. (2)
127

141
CHAPTER 4
将方程(2)的左边配方,并把常数项移到右边,得
①
(Ⅰ) 当 时,比较方程 ① 和圆的标准方程,可以看出方程(2)表示以为圆心,为半径长的圆;
(Ⅱ) 当 时,方程(2)只有实数解 ,,它表示一个点;
(Ⅲ) 当 时,方程(2)没有实数解,它不表示任何图形。
因此,当 时,方程(2)表示一个圆。
方程(2)叫做圆的一般方程(general equation of circle)。
思考
圆的标准方程与圆的一般方程各有什么特点?
例 4
求过三点 O(0, 0), M₁(1, 1), M₂(4, 2)的圆的方程,并求这个圆的半径长和圆心坐标。
**分析:**由于 O(0, 0), M₁(1, 1), M₂(4, 2)不在同一条直线上,因此经过 O, M₁, M₂ 三点有唯一的圆。
**解:**设圆的方程是
. ①
因为 O, M₁, M₂ 三点都在圆上,所以它们的坐标都是方程 ① 的解。把它们的坐标依次代入方程 ①,得到关于 D, E, F 的一个三元一次方程组
解这个方程组,得
D = -8, E = -6, F = 0.
所以,所求圆的方程是
.

142
第四章 圆与方程
例 5
已知线段 AB 的端点 B 的坐标是(4,3),端点 A 在圆上运动,求线段 AB 的中点 M 的轨迹方程。
分析: 如图 4.1-4,点 A 运动引起点 M 运动,而点 A 在已知圆上运动,点 A 的坐标满足方程。建立点 M 与点 A 坐标之间的关系,就可以建立点 M 的坐标满足的条件,求出点 M 的轨迹方程。
解: 设点 M 的坐标是(x,y),点 A 的坐标是()。由于点 B 的坐标是(4,3),且 M 是线段 AB 的中点,所以
,。
于是有
,。 ①
因为点 A 在圆上运动,所以点 A 的坐标满足方程
, 即 。 ②
把 ① 代入 ②,得
。
整理,得
。
所以,点 M 的轨迹是以为圆心,半径长是 1 的圆。
129

143
练习
求下列各方程表示的圆的圆心坐标和半径长:
(1) ;
(2) ;
(3) .判断下列方程分别表示什么图形:
(1) ;
(2) ;
(3) .如图,等腰梯形 ABCD 的底边长分别为 6 和 4,高为 3,求这个等腰梯形的外接圆的方程,并求这个圆的圆心坐标和半径长。
第 3 题
习题 4.1 A 组
求下列各圆的圆心坐标和半径长,并画出它们的图形:
(1) ;
(2) ;
(3) ;
(4) .求下列各圆的方程,并画出图形:
(1) 圆心为点 C(8,-3),且过点 A(5,1);
(2) 过 A(-1, 5), B(5, 5), C(6,-2)三点.已知圆 C 的圆心在直线 l: 上,并且经过原点和 A(2,1),求圆 C 的标准方程.
圆 C 的圆心在 x 轴上,并且过点 A(-1,1)和 B(1,3),求圆 C 的方程.
已知圆的一条直径的端点分别是 A(), B(),求证此圆的方程是
.△ABC 的顶点 B, C 的坐标分别是(-3,-1), (2,1), 顶点 A 在圆上运动,求 △ABC 的重心 G 的轨迹方程.
平面直角坐标系中有 A(0,1), B(2, 1), C(3, 4), D(-1,2)四点,这四点能否在同一个圆上?为什么?

144
第四章 圆与方程
B 组
等腰三角形的顶点 A 的坐标是(4, 2), 底边一个端点 B 的坐标是(3, 5), 求另一个端点 C 的轨迹方程,并说明它是什么图形。
长为 2a 的线段 AB 的两个端点 A 和 B 分别在 x 轴和 y 轴上滑动,求线段 AB 的中点的轨迹方程。
已知点 M 与两个定点 O(0, 0), A(3, 0)的距离的比为,先利用信息技术手段,探求点 M 的轨迹,然后求出它的方程。
坐标法与机器证明
笛卡儿(Descartes, 1596—1650)创立坐标系,使几何问题的求解或求证通过坐标转化为代数方程求解,代数方程的求解是一个计算问题,有了坐标,使计算机进入到几何定理的证明中来成为可能。
明确提出机器可以成为推理工具的思想,要追溯到 17 世纪德国数学家莱布尼兹(Leibniz, 1646—1716,微积分创始人之一)。他受笛卡儿思想的启发,认为笛卡儿创立的解析几何,目的是将几何推理转化为计算,遗憾的是,由于当时的条件限制,计算仅仅是手工操作(手摇计算机),无法进行大量复杂的计算,所以用机器实现几何定理证明的想法无法实现。
20 世纪以后,计算机迅速发展,计算机的发明使一些数学家又开始探讨几何定理证明机械化的可能性。1950 年,波兰数学家塔斯基得到一个引人注目的结论:一切初等几何范畴中的命题都可以用机械方法判定。由于他的判定方法太复杂,在实践中没有太大的进展。1959 年,美籍华裔数学家王浩(1921—1999)在这方面做出了鼓舞人心的工作,他在计算机上只用了 9 分钟就证明了《数学原理》(罗素和怀特海著)中的 350 多个命题,并第一次明确提出了“走向数学的机械化”的口号。
20 世纪 70 年代以后,我国著名数学家吴文俊在几何定理机器证明上作出了重大贡献,并创立了“吴方法”。
● 中科院院士,在拓扑学、自动推理、机器证明、代数几何、中国数学史、对策论等研究领域均有杰出的贡献。2001 年获首届国家最高科学技术奖。
131

145
CHAPTER 1
普通高中课程标准实验教科书 数学 2
吴文俊机器证明的思想,主要是从笛卡儿的坐标法和中国古代解方程的计算方法而来的,他认为,欧氏几何体系的特点是纯粹在空间形式间推理,或说在图形之间,或者是把数量关系归之于空间形式,或者干脆排除掉数量关系,另一个体系刚好与之相反,是把空间形式转化成数量关系来处理。这种考虑方式就是中国的传统,早在 11 世纪左右就已产生,当时引进的概念叫天元、地元等,用现在的符号就相当于引进了 x,y 等,用天元、地元表示某一个几何事实,那么几何对象之间的相互关系就表示成天元、地元之间的一种方程(即 x,y 之间的一种方程),即 17 世纪解析几何的坐标法。
吴文俊认为,欧氏几何体系是非机械化的,把空间形式数量化是机械化的。吴文俊说:“对于几何,对于研究空间形式,你要真正腾飞,不通过数量关系,我想不出有什么好办法。”“我从事几何定理证明时,首先取适当的坐标,于是几何定理的假设与结论通常都成为多项式方程,称之为假设方程与结论方程。满足定理假设的几何图象,就相当于假设方程组的一个解答或零点。要证明定理成立,就是要证明假设方程的零点也使结论多项式为零。”由于计算机的发展与众多数学家(特别是以吴文俊为首的一批中国数学家)的努力,大约在 1976 与 1977 年之交,几何定理机器证明的梦想终于实现了。
132
