Skip to main content

1.1　算法与程序框图

Tong LiJanuary 23, 2025About 11 min

1.1　算法与程序框图

14

CHAPTER 1

1.1 算法与程序框图

1.1.1 算法的概念

实际上，算法对我们来说并不陌生。

回顾二元一次方程组
{x−2y=−1,2x+y=1\begin{cases} x-2y=-1, \\ 2x+y=1 \end{cases} ① ②

的求解过程，我们可以归纳出以下步骤：

第一步：②−-①$\times$2，得
5y = 3；

第二步：解③得 y=35y = \frac{3}{5}；

第三步：将 y=35y = \frac{3}{5} 代入①，得 x=15x = \frac{1}{5}。

对于一般的二元一次方程组
{a1x+b1y=c1,a2x+b2y=c2,\begin{cases} a_1x+b_1y=c_1, \\ a_2x+b_2y=c_2, \end{cases}

其中 a1b2−a2b1≠0a_1b_2-a_2b_1 \neq 0，也可以按照上述步骤来求解，这些步骤就构成了解二元一次方程组的算法，我们可以根据这一算法编制计算机程序，让计算机来解二元一次方程组。

思考

对于一般的二元一次方程组来说，上述步骤应该怎样进一步完善？

14
15

第一章 算法初步

算法 (algorithm)

●据说英文 algorithm 来源于阿拉伯数学家花拉子米的拉丁译名 Algoritmi.

●只能被1和自身整除的大于1的整数叫质数.

算法 (algorithm) 这个词出现于12世纪，指的是用阿拉伯数字进行算术运算的过程。在数学中，现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成。

按照这样的理解，我们可以设计出很多具体数学问题的算法，下面看几个例子：

例 1

任意给定一个大于1的整数 n，试设计一个程序或步骤对 n 是否为质数做出判定。

算法分析: 根据质数的定义，很容易设计出下面的步骤：

步骤:

第一步：判断 n 是否等于 2。若 n=2，则是质数；若 n>2，则执行第二步。

第二步：依次从 2~(n-1) 检验是不是 n 的因数，即整除 n 的数。若有这样的数，则 n 不是质数；若没有这样的数，则 n 是质数。

这是判断一个大于 1 的整数 n 是否为质数的最基本算法。

例 2

用二分法设计一个求方程 x2−2=0x^2 - 2 = 0 的近似根的算法。

算法分析: 回顾二分法解方程的过程，并假设所求近似根与精确解的差的绝对值不超过 0.005，则不难设计出以下步骤：

步骤:

第一步：令 f(x)=x2−2f(x) = x^2 - 2。因为 f(1)<0f(1) < 0，f(2)>0f(2) > 0，所以设 x1=1x_1 = 1，x2=2x_2 = 2。

第二步：令 m=x1+x22m = \frac{x_1 + x_2}{2}，判断 f(m)f(m) 是否为 0。若是，则 m 为所求；若否，则继续判断 f(x1)⋅f(m)f(x_1) \cdot f(m) 大于 0 还是小于 0。

第三步：若 f(x1)⋅f(m)>0f(x_1) \cdot f(m) > 0，则令 x1=mx_1 = m；否则，令 x2=mx_2 = m。

第四步：判断 ∣x1−x2∣<0.005|x_1 - x_2| < 0.005 是否成立？若是，则 x1x_1、x2x_2 之间的任意取值均为满足条件的近似根；若否，则……

3

15
16

CHAPTER

普通高中课程标准实验教科书 数学 3

返回第二步。

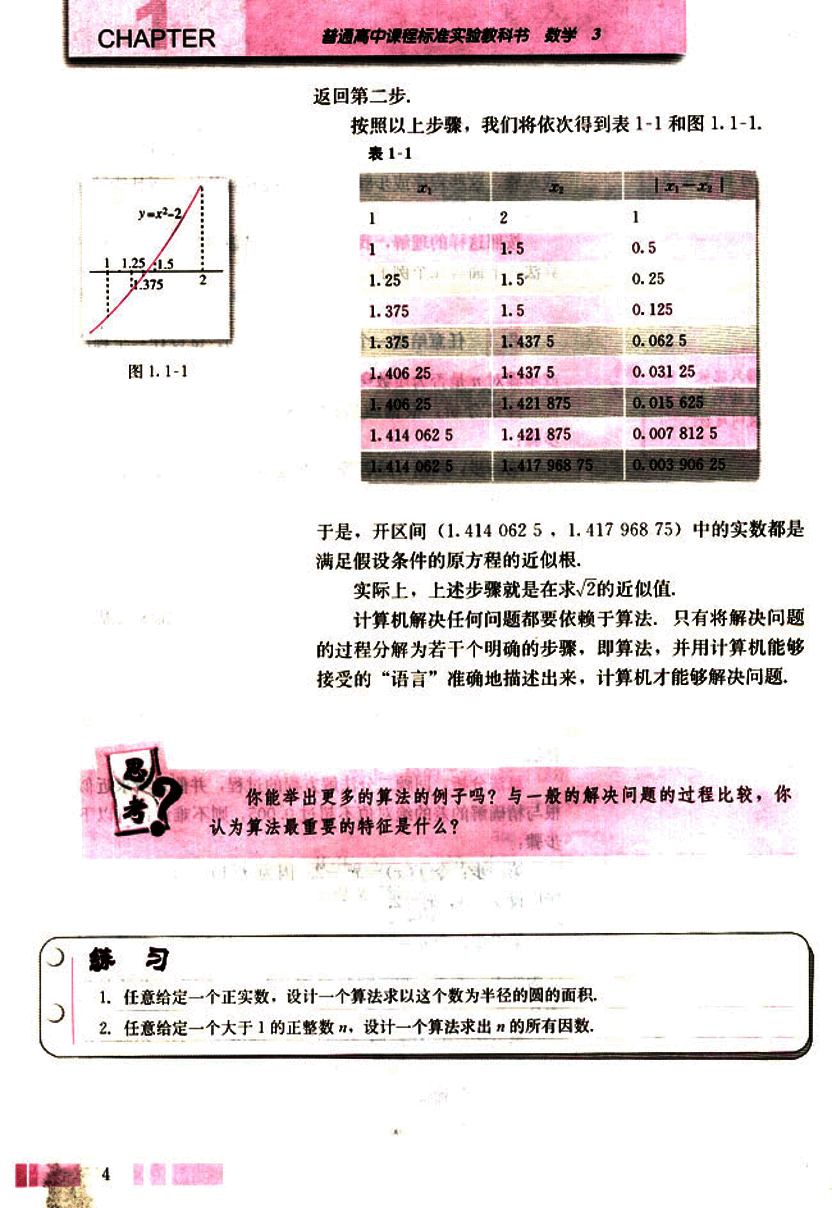
按照以上步骤，我们将依次得到表1-1和图1.1-1。

表1-1

| x1x_1 | x2x_2 | ∣x1−x2∣|x_1 - x_2| |
|---|---|---|
| 1 | 2 | 1 |
| 1.25 | 1.5 | 0.25 |
| 1.375 | 1.5 | 0.125 |
| 1.375 | 1.437 5 | 0.062 5 |
| 1.406 25 | 1.437 5 | 0.031 25 |
| 1.406 25 | 1.421 875 | 0.015 625 |
| 1.414 062 5 | 1.421 875 | 0.007 812 5 |
| 1.414 062 5 | 1.417 968 75 | 0.003 906 25 |

于是，开区间(1.414 062 5，1.417 968 75)中的实数都是满足假设条件的原方程的近似根。

实际上，上述步骤就是在求2\sqrt{2}的近似值。

计算机解决任何问题都要依赖于算法，只有将解决问题的过程分解为若干个明确的步骤，即算法，并用计算机能够接受的“语言”准确地描述出来，计算机才能够解决问题。

你能举出更多的算法的例子吗？与一般的解决问题的过程比较，你认为算法最重要的特征是什么？

练习

  1. 任意给定一个正实数，设计一个算法求以这个数为半径的圆的面积。
  2. 任意给定一个大于1的正整数，设计一个算法求出n的所有因数。

16
17

第一章 算法初步

1.1.2 程序框图

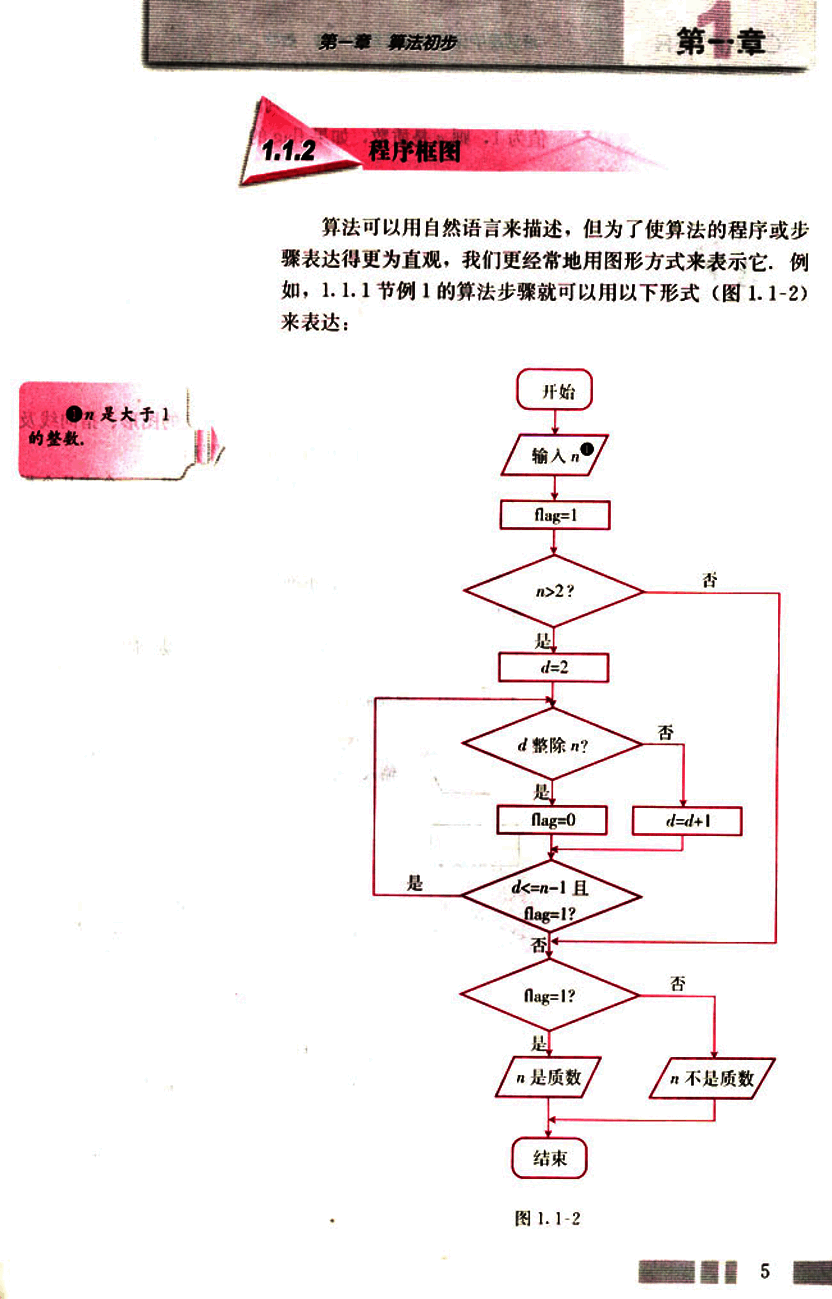
算法可以用自然语言来描述，但为了使算法的程序或步骤表达得更为直观，我们更经常地用图形方式来表示它，例如，1.1.1节例1的算法步骤就可以用以下形式（图1.1-2）来表达：

开始
输入n
flag=1
n>2?
否
是
d=2
d整除n?
否
是
flag=0
d=d+1
d<=n-1且
flag=1?
否
是
flag=1?
否
是
n是质数
n不是质数
结束

图1.1-2

5

17
18

CHAPTER

普通高中课程标准实验教科书 数学 3

框图中的flag 是用来记录判断结果的，如果最后flag的值为1，则 是质数，如果flag 的值为0，则不是质数。

  1. 框图中的d有什么作用？d=d+1是怎么回事儿？
  2. 通过以上算法的两种不同表达方式的比较，你觉得用程序框图来表达算法有哪些特点？

程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。

通常，程序框图由程序框和流程线组成。一个或几个程序框的组合表示算法中的一个步骤；流程线是方向箭头，按照算法进行的顺序将程序框连接起来。表1-2列出了几个基本程序框和它们各自表示的功能。

表1-2

程序框名称功能
image1终端框（起止框）表示一个算法的起始和结束
image2输入、输出框表示一个算法输入和输出的信息
image3处理框（执行框）赋值、计算
image4判断框判断某一条件是否成立，成立时在出口处标明“是”或“Y”；不成立时标明“否”或“N”。

用程序框图来表达算法，算法的基本逻辑结构展现得很清楚。从上面的程序框图中，不难看出以下三种不同的基本逻辑结构：

18
19

第一章 算法初步

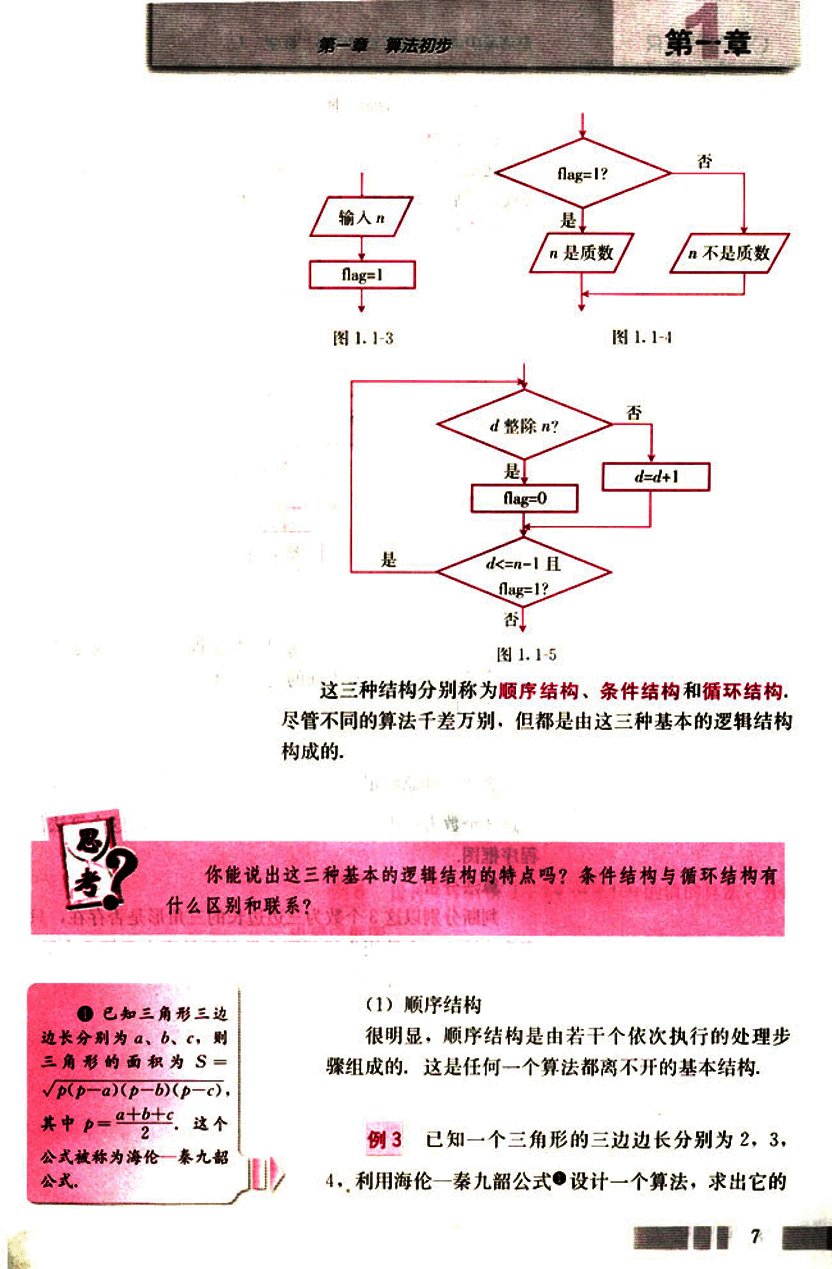
三种基本逻辑结构

图1.1-3

input_n

-> flag=1

图1.1-4

flag=1?

是 -> n是质数

否 -> n不是质数

图1.1-5

d整除n?

否 -> d=d+1

是 -> flag=0

d<=n-1且flag=1?

是

否

这三种结构分别称为顺序结构、条件结构和循环结构。尽管不同的算法千差万别，但都是由这三种基本的逻辑结构构成的。

你能说出这三种基本的逻辑结构的特点吗？条件结构与循环结构有什么区别和联系？

(1)顺序结构

很明显，顺序结构是由若干个依次执行的处理步骤组成的，这是任何一个算法都离不开的基本结构。

例3 已知一个三角形的三边边长分别为2，3，4。利用海伦—秦九韶公式设计一个算法，求出它的

● 已知三角形三边长分别为a、b、c，则三角形的面积为S=p(p−a)(p−b)(p−c)\sqrt{p(p-a)(p-b)(p-c)}，其中p=a+b+c2\frac{a+b+c}{2}。这个公式被称为海伦—秦九韶公式。

19
20

CHAPTER 1

普通高中课程标准实验教科书 数学 3

面积，画出算法的程序框图。

算法分析：

这是一个简单的问题，只需先算出 pp 的值，再将它代入公式，最后输出结果。只用顺序结构就能够表达出算法。

程序框图：

graph TD
    A[开始] --> B{p = (2+3+4)/2};
    B --> C{S = √[p(p-2)(p-3)(p-4)]};
    C --> D[输出 S];
    D --> E[结束];

(2) 条件结构

在一个算法中，经常会遇到一些条件的判断，算法的流程根据条件是否成立有不同的流向，条件结构就是处理这种过程的结构。

例 4

任意给定 3 个正实数，设计一个算法，判断分别以这 3 个数为三边边长的三角形是否存在，画出这个算法的程序框图。

算法分析：

判断分别以这 3 个数为三边边长的三角形是否存在，只需要验证这 3 个数当中任意两个数的和是否大于第 3 个数。这就需要用到条件结构。

20
21

第一章 算法初步

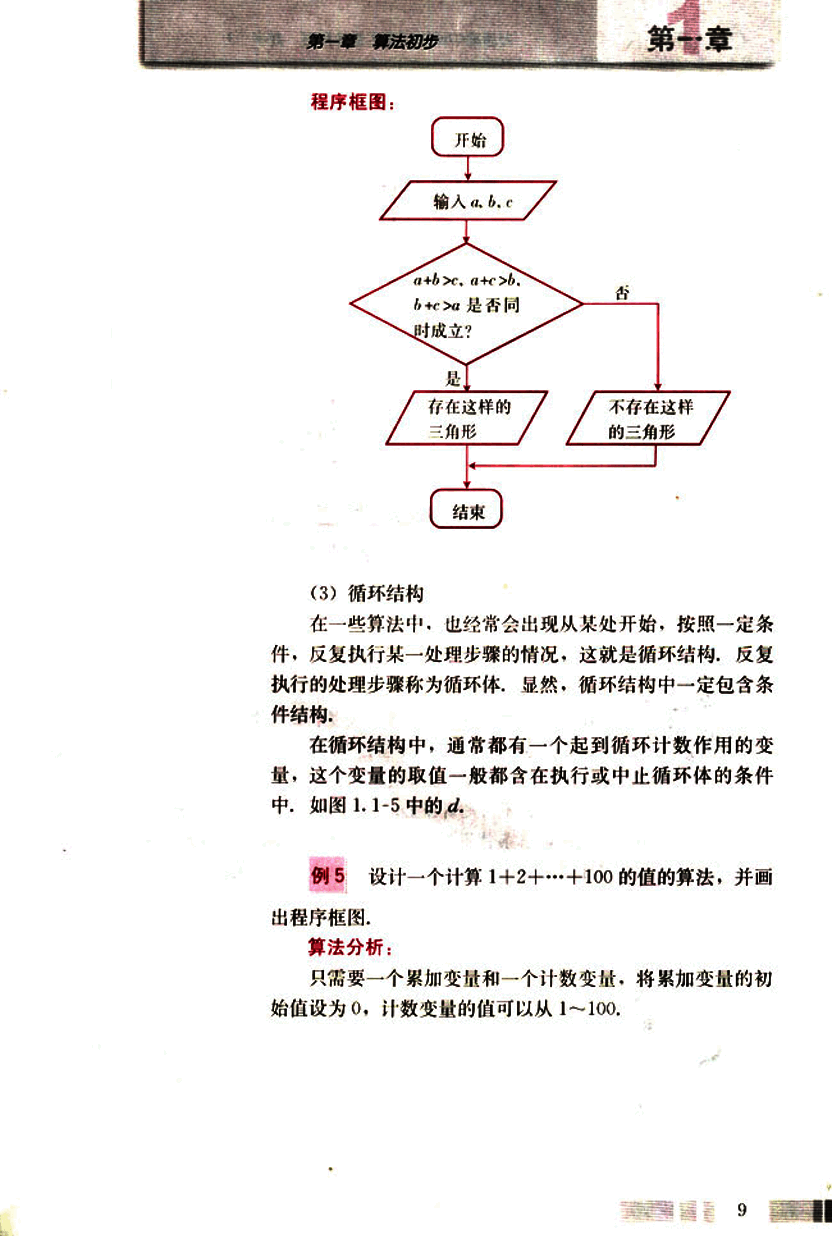
程序框图:

graph TD
    A[开始] --> B{输入a,b,c};
    B --> C{a+b>c, a+c>b, b+c>a 是否同时成立?};
    C -- 是 --> D[存在这样的三角形];
    C -- 否 --> E[不存在这样的三角形];
    D --> F[结束];
    E --> F;

(3) 循环结构

在一些算法中，也经常会出现从某处开始，按照一定条件，反复执行某一处理步骤的情况，这就是循环结构，反复执行的处理步骤称为循环体。显然，循环结构中一定包含条件结构。

在循环结构中，通常都有一个起到循环计数作用的变量，这个变量的取值一般都含在执行或中止循环体的条件中，如图1.1-5中的d。

例5

设计一个计算1+2+…………+100的值的算法，并画出程序框图。

算法分析：

只需要一个累加变量和一个计数变量，将累加变量的初始值设为0，计数变量的值可以从1～100。

9

21
22

CHAPTER 1

普通高中课程标准实验教科书 数学 3

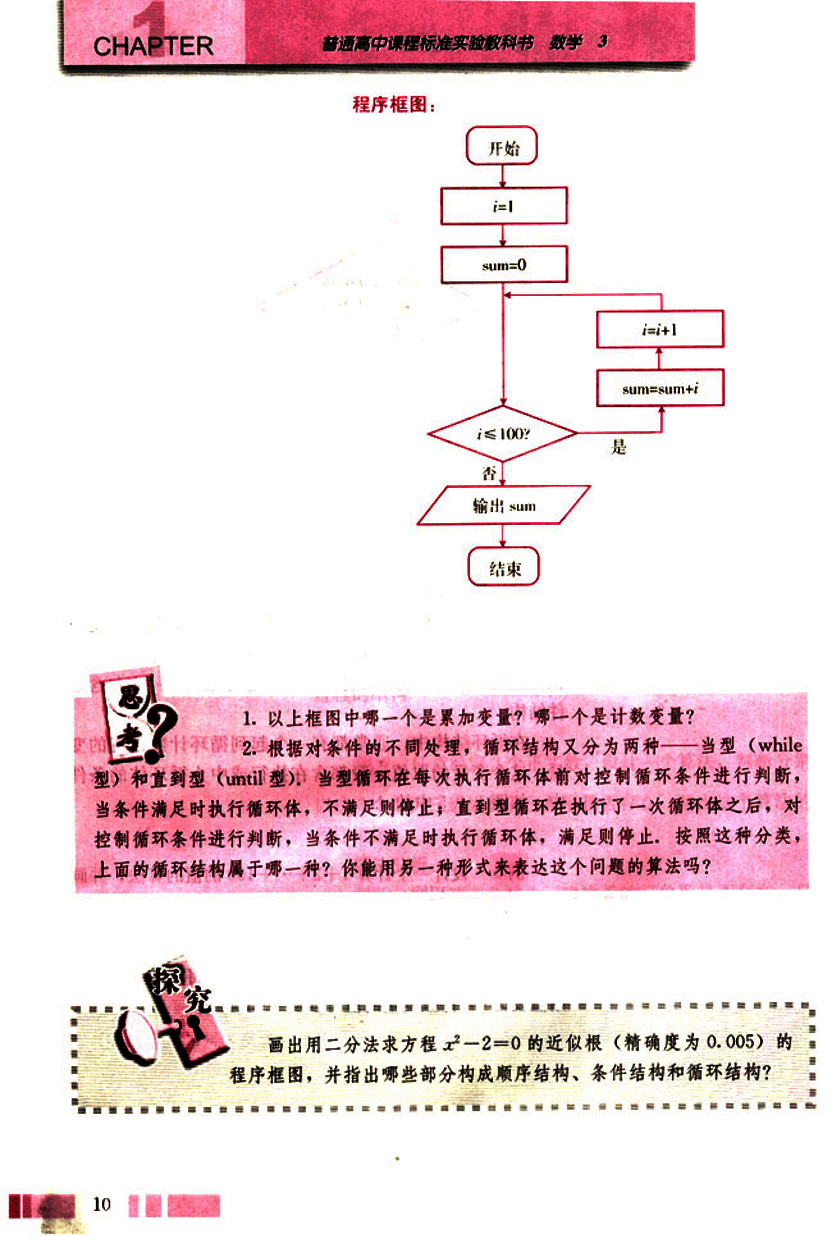
程序框图:

graph TD
    A[开始] --> B{i=1};
    B --> C{sum=0};
    C --> D{i ≤ 100?};
    D -- 是 --> E{sum = sum + i};
    E --> F{i = i + 1};
    F --> D;
    D -- 否 --> G[输出 sum];
    G --> H[结束];

思考

  1. 以上框图中哪一个是累加变量？哪一个是计数变量？

  2. 根据对条件的不同处理，循环结构又分为两种——当型（while型）和直到型（until型），当型循环在每次执行循环体前对控制循环条件进行判断，当条件满足时执行循环体，不满足则停止；直到型循环在执行了一次循环体之后，对控制循环条件进行判断，当条件不满足时执行循环体，满足则停止。按照这种分类，上面的循环结构属于哪一种？你能用另一种形式来表达这个问题的算法吗？

探究

画出用二分法求方程 x2−2=0x^2 - 2 = 0 的近似根（精确度为 0.005）的程序框图，并指出哪些部分构成顺序结构、条件结构和循环结构？

22
23

第一章 算法初步

第一章

练习

  1. 设计一个求任意数的绝对值的算法，并画出程序框图。
  2. 利用二分法设计一个算法求3\sqrt{3}的近似值，并画出程序框图。

习题 1.1

A 组

  1. 找一个实际生活中的分段函数，设计一个求该函数值的算法，并画出程序框图。
  2. 设计一个算法求12+22+……+992+10021^2+2^2+……+99^2+100^2的值，并画出程序框图。
  3. 某居民区的物业部门每月向居民收取卫生费，计费方法是：3人和3人以下的住户，每户收取5元；超过3人的住户，每超出1人加收1.2元。设计一个算法，根据输入的人数，计算应收取的卫生费，并画出程序框图。

B 组

  1. 某高中男子体育小组的50米跑成绩（单位：s）为：
    6.4, 6.5, 7.0, 6.8, 7.1, 7.3, 6.9, 7.4, 7.5.
    设计一个算法，从这些成绩中搜索出小于6.8s的成绩，并画出程序框图。
  2. 设计一个求解一般二元一次方程组的算法，并画出程序框图。

11

23
23
Default footer
Copyright © 2025 Tong Li