1.1.2 弧度制

Tong LiJanuary 23, 2025About 9 min

1.1.2 弧度制

CHAPTER 练习

(口答)锐角是第几象限角？第一象限角一定是锐角吗？再分别就直角、钝角来回答这两个问题。
(口答)今天是星期三，那么7k(k∈Z)天后的那一天是星期几？7k(k∈Z)天前的那一天是星期几？100天后的那一天是星期几？
已知角的顶点与直角坐标系的原点重合，始边与x轴的非负半轴重合，作出下列各角，并指出它们是第几象限角：
(1) 420°； (2) -75°； (3) 855°； (4) -510°。
在0°～360°范围内，找出与下列各角终边相同的角，并指出它们是第几象限角：
(1) -54°18′； (2) 395°8′； (3) -1 190°30′。
写出与下列各角终边相同的角的集合，并把集合中适合不等式 -720° < β < 360° 的元素写出来：
(1) 1 303°18′； (2) -225°。

1.1.2 弧度制

度量长度可以用米、尺、码等不同的单位制，度量重量可以用千克、斤、磅等不同的单位制，不同的单位制能解决问题带来方便，角的度量是否也能用不同的单位制呢？

我们知道，角可以用度为单位进行度量，1度的角等于周角的 $\frac{1}{360}$ 。这种用度作为单位来度量角的单位制叫做角度制(degree measure)。为了使用方便，数学上还采用另一种度量角的单位制——弧度制(radian measure)：

把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角，用符号 rad 表示，读作弧度。

如图 1.1-8，圆O的半径为1，AB的长等于1，∠AOB 就是1弧度的角。

第一章三角函数

第一章

如图1.1-9,半径为r的圆的圆心与原点重合，角α的始边与x轴的正半轴重合，交圆于点A，终边与圆交于点B.请在下列表格中填空，并思考：如果一个半径为r的圆的圆心角α所对的弧长是l，那么α的弧度数是多少？既然角度制、弧度制都是角的度量制，那么它们之间如何换算？

表1.1-1

AB的长	OB旋转的方向	∠AOB的弧度数	∠AOB的度数
πr	逆时针方向	1	180°
2r	逆时针方向	2	360°
r	逆时针方向	$\frac{1}{2}$	90°
2r	反时针方向	$-\frac{\pi}{2}$	-90°

图1.1-9

6世纪，印度人在制作正弦表时，曾用同一单位度量半径和圆周，孕育着最早的弧度制概念，欧拉是明确提出弧度制思想的数学家，1748年，在他的一部划时代著作《无穷小分析概论》中，提出把圆的半径作为弧长的度量单位，使一个圆周角等于2π弧度，1弧度等于周角的 $\frac{1}{2\pi}$ ，这一思想将线段与弧的度量统一起来，大大简化了三角公式及计算。

一般地，正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0.如果半径为r的圆的圆心角α所对弧的长为l，那么，角α的弧度数的绝对值是

$|α| = \frac{l}{r}$

这里，α的正负由α的终边的旋转方向决定。

用角度制和弧度制来度量零角，单位不同，但量数相同（都是0）；用角度制和弧度制度量任一非零角，单位不同，量数也不同。因为周角的弧度数是2π，而在角度制下的度数是360，所以

360° = 2π rad.

180° = π rad.

1° = $\frac{\pi}{180}$ rad ≈0.017 45 rad.

反过来有：

1 rad = ( $\frac{180}{\pi}$ )° ≈57.30° = 57°18′.

一般地，我们只需根据
7

CHAPTER

普通高中课程标准实验教科书数学 4

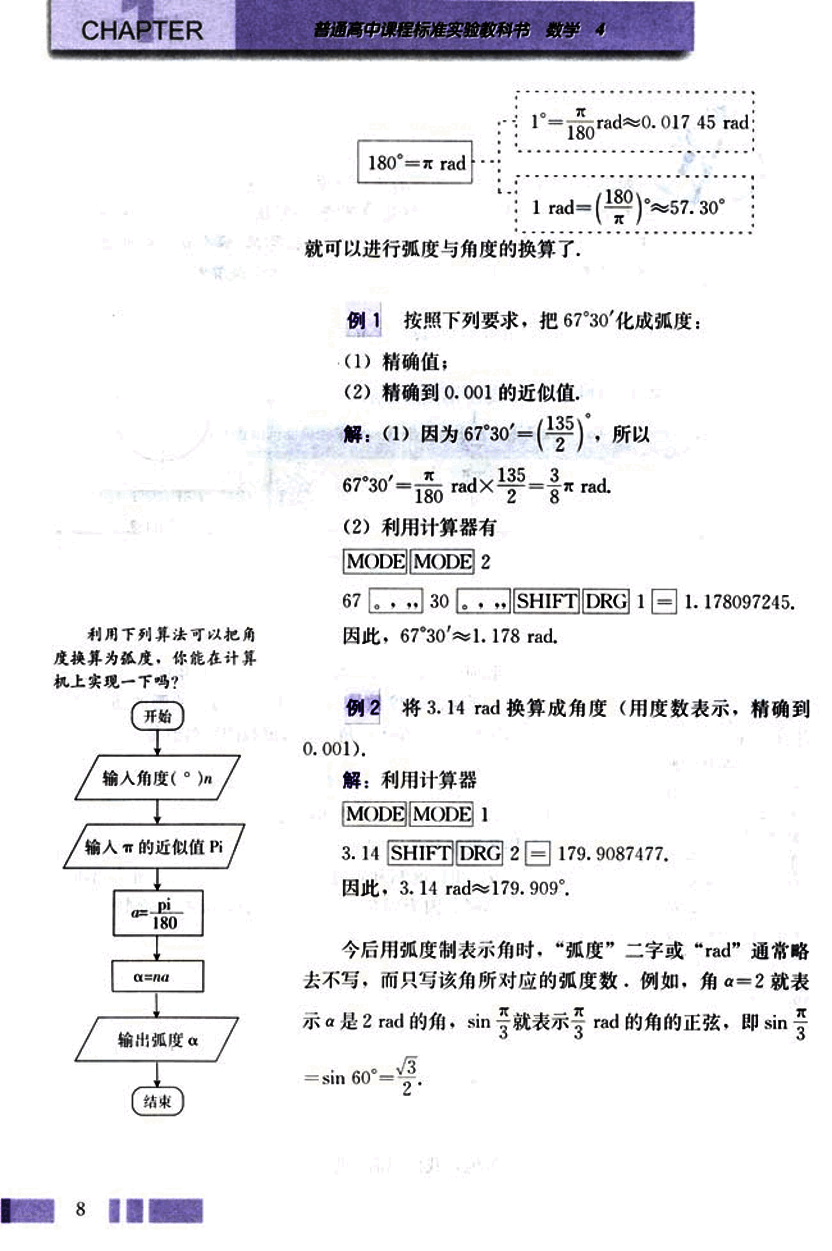
180°=π rad

1° = $\frac{π}{180}$ rad ≈ 0.017 45 rad

1 rad = $(\frac{180}{π})°$ ≈ 57.30°

就可以进行弧度与角度的换算了。

例 1

按照下列要求，把67°30′化成弧度：

(1) 精确值；

(2) 精确到0.001的近似值.

解：(1) 因为67°30′= $(\frac{135}{2})°$ ，所以

67°30′ = $\frac{π}{180}$ rad × $\frac{135}{2}$ = $\frac{3}{8}$ π rad.

(2) 利用计算器有

MODE MODE 2

67 ... ... 30 ... ... SHIFT DRG 1 = 1.178097245.

因此，67°30′ ≈ 1.178 rad.

例 2

将 3.14 rad 换算成角度（用度数表示，精确到 0.001）。

解：利用计算器

MODE MODE 1

3.14 SHIFT DRG 2 = 179.9087477.

因此，3.14 rad ≈ 179.909°.

今后用弧度制表示角时，“弧度”二字或 “rad” 通常略去不写，而只写该角所对应的弧度数。例如，α = 2 就表示 α 是 2 rad 的角，sin $\frac{π}{3}$ 表示 $\frac{π}{3}$ rad 的角的正弦，即 sin $\frac{π}{3}$ = sin 60° = $\frac{\sqrt{3}}{2}$ 。

第一章三角函数

第一节

填写下列特殊角的度数与弧度数的对应表：

度	0°	30°	45°	120°	135°	150°	360°
弧度				$\frac{\pi}{3}$	$\frac{2\pi}{3}$	$\frac{\pi}{2}$	$2\pi$

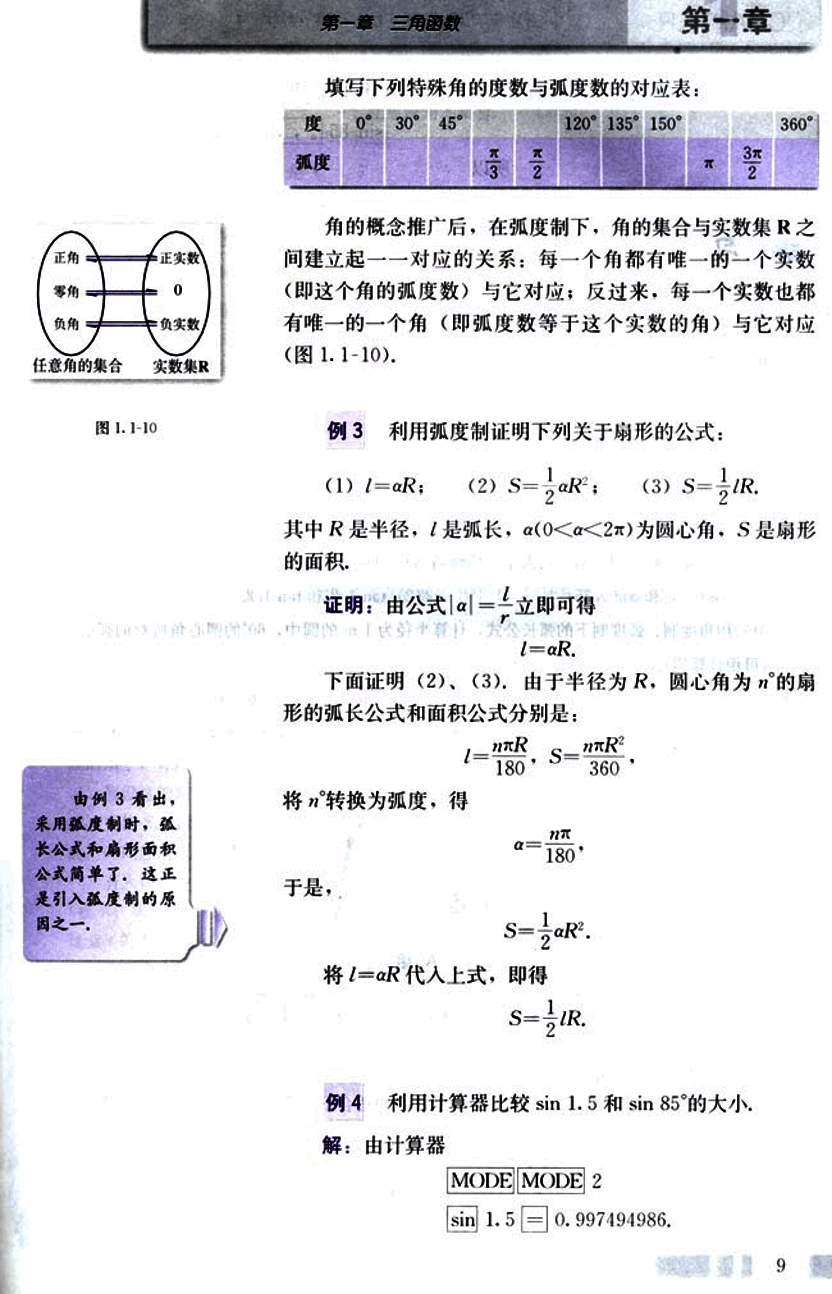
角的概念推广后，在弧度制下，角的集合与实数集R之间建立起一一对应的关系：每一个角都有唯一的一个实数（即这个角的弧度数）与它对应；反过来，每一个实数也都有唯一的一个角（即弧度数等于这个实数的角）与它对应（图 1.1-10）。

图1.1-10

例3

利用弧度制证明下列关于扇形的公式：

(1) $l = aR$ ;

(2) $S = \frac{1}{2}aR^2$ ;

(3) $S = \frac{1}{2}lR$ .

其中R是半径，l是弧长， $a(0 < a < 2\pi)$ 为圆心角，S是扇形的面积。

证明：由公式 $|a| = \frac{l}{R}$ 立即可得

$l = aR$ .

下面证明 (2)、(3)。由于半径为R，圆心角为n的扇形的弧长公式和面积公式分别是：

$l = \frac{n\pi R}{180}$ , $S = \frac{n\pi R^2}{360}$ .

将n转换为弧度，得

$a = \frac{n\pi}{180}$ .

于是，

$S = \frac{1}{2}aR^2$ .

将 $l = aR$ 代入上式，即得

$S = \frac{1}{2}lR$ .

例4

利用计算器比较sin 1.5 和 sin 85°的大小。

解：由计算器

MODE MODE 2

sin 1.5 = 0.997494986.

练习

把下列角度化成弧度：
(1) 22°30′；
(2) -210°；
(3) 1 200°.
把下列弧度化成度：
(1) $\frac{\pi}{12}$ ；
(2) $\frac{4\pi}{3}$ ；
(3) $\frac{3\pi}{10}$
用弧度表示：
(1) 终边在x轴上的角的集合；
(2) 终边在y轴上的角的集合。
利用计算器比较下列各对值的大小（精确到0.001）：
(1) cos 0.75°和 cos 0.75；
(2) tan 1.2°和 tan 1.2。
分别用角度制、弧度制下的弧长公式，计算半径为1 m的圆中，60°的圆心角所对的弧的长度
(可用计算器)。
已知半径为120 mm的圆上，有一条弧的长是144 mm，求该弧所对的圆心角的弧度数。

习题 1.1 A组

在0°～360°范围内，找出与下列各角终边相同的角，并指出它们是哪个象限的角：
(1) -265°； (2) -1000°； (3) -843°10′； (4) 3 900°。
写出终边在x轴上的角的集合。
写出与下列各角终边相同的角的集合，并把集合中适合不等式 -360° < β < 360° 的元素写出来：
(1) 60°； (2) -75°； (3) -824°30′； (4) 475°； (5) 90°； (6) 270°； (7) 180°； (8) 0°。