24
我们已经学过锐角三角函数,知道它们都是以锐角为自变量,以比值为函数值的函数。你能用直角坐标系中角的终边上点的坐标来表示锐角三角函数吗?
如图 1.2-1,设锐角α的顶点与原点O重合,始边与x轴的正半轴重合,那么它的终边在第一象限。在α的终边上任取一点P(a, b), 它与原点的距离 r = a 2 + b 2 > 0 r = \sqrt{a^2 + b^2} > 0 r = a 2 + b 2 > 0
image
图 1.2-1
根据初中学过的三角函数定义,我们有
12
sin α = MP/OP = b/r, cos α = OM/OP = a/r, tan α = MP/OM = b/a
由相似三角形的知识,对于确定的角α,这三个比值不会随点P在α的终边上的位置的改变而改变,因此我们可以将点P取在使线段OP的长r=1的特殊位置上(如图1.2-2)。这样就可以得到用直角坐标系内点的坐标表示的锐角三角函数:
sin α = MP/OP = b, cos α = OM/OP = a, tan α = MP/OM = b/a
图1.2-2
在引进弧度制时我们看到,在半径为单位长的圆中,角α的弧度数的绝对值等于圆心角所对的弧长(符号由α的终边的旋转方向决定)。在直角坐标系中,我们称以原点O为圆心,以单位长度为半径的圆为单位圆 (unit circle)。这样,上述P点就是α的终边与单位圆的交点。锐角三角函数可以用单位圆上点的坐标表示。
同样的,我们可以利用单位圆定义任意角的三角函数。
如图1.2-3,设α是一个任意角,它的终边与单位圆交于点P(x, y), 那么:
(1) y叫α的正弦(sine),记作sin α,即 sin α = y;
(2) x叫α的余弦(cosine),记作cos α,即 cos α = x;
(3) y/x叫α的正切(tangent),记作tan α,即 tan α = y/x (x ≠ 0).
可以看出,当 α = π/2 + kπ (k∈Z) 时,α的终边在y轴上。
图1.2-3
13
这时点P的横坐标x等于0,所以tanα=无意义。除此以外,对于确定的角α,上述三个值都是唯一确定的,所以,正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数(trigonometric function)。由于角的集合与实数集之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数。
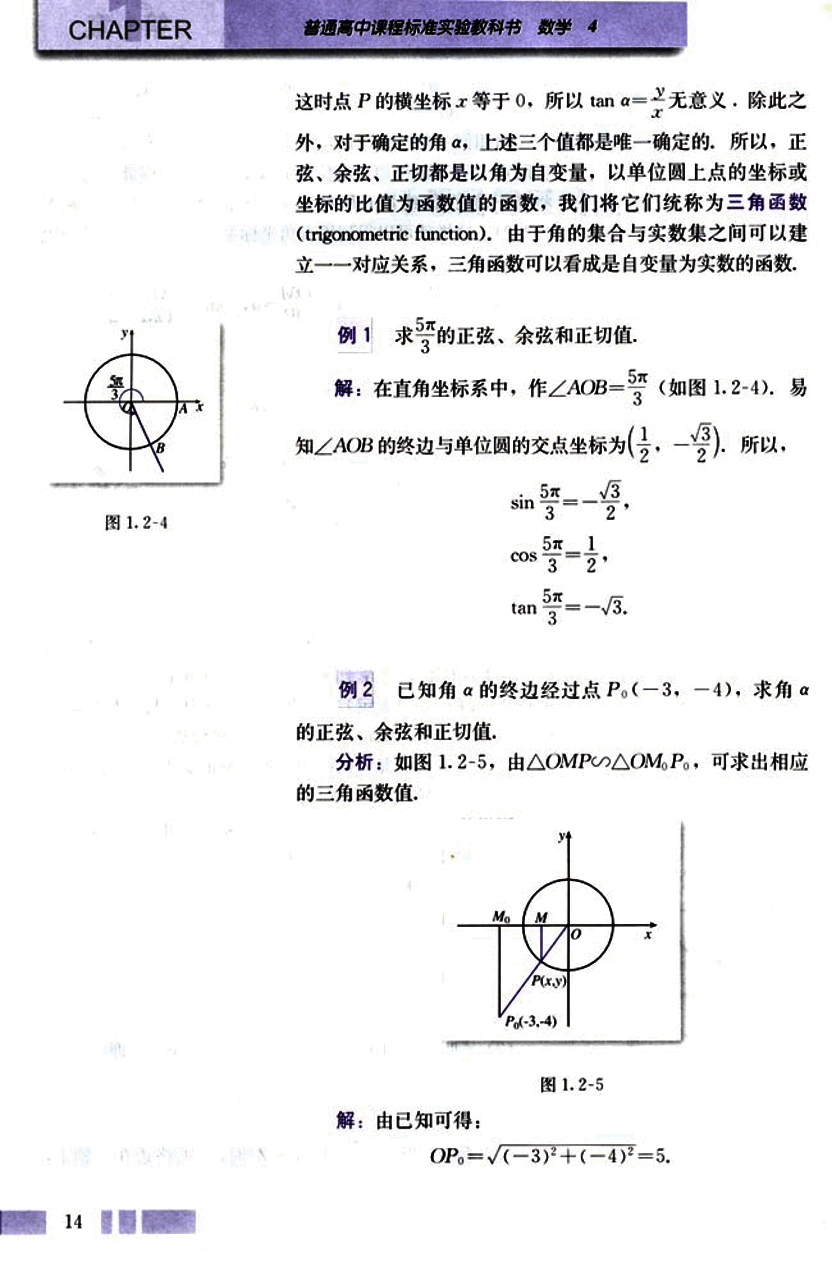
求5 π 3 \frac{5\pi}{3} 3 5 π
解:在直角坐标系中,作∠AOB=5 π 3 \frac{5\pi}{3} 3 5 π 1 2 \frac{1}{2} 2 1 − 3 2 -\frac{\sqrt{3}}{2} − 2 3
sin5 π 3 \frac{5\pi}{3} 3 5 π − 3 2 -\frac{\sqrt{3}}{2} − 2 3
cos5 π 3 \frac{5\pi}{3} 3 5 π 1 2 \frac{1}{2} 2 1
tan5 π 3 \frac{5\pi}{3} 3 5 π − 3 -\sqrt{3} − 3
图1.2-4
已知角α的终边经过点P 0 P_0 P 0
分析:如图1.2-5,由△OMP ∽ △OMP0 _0 0
图1.2-5
解:由已知可得:
O P 0 OP_0 O P 0 ( − 3 ) 2 + ( − 4 ) 2 \sqrt{(-3)^2+(-4)^2} ( − 3 ) 2 + ( − 4 ) 2
14
如图1.2-5,设角α的终边与单位圆交于点P(x, y)。分别过点P、P0 作x轴的垂线MP、M0 P0 ,则
|M0 P0 | = 4,|MP| = -y,
|OM| = 3,|OM| = -x,
△OMP ≅ △OM0 P0 。
于是,
sin α = y = -M P O P \frac{MP}{OP} OP MP ∣ M 0 P 0 ∣ ∣ O P 0 ∣ \frac{|M_0P_0|}{|OP_0|} ∣ O P 0 ∣ ∣ M 0 P 0 ∣ 4 5 \frac{4}{5} 5 4
cos α = x = -O M O P \frac{OM}{OP} OP OM ∣ O M 0 ∣ ∣ O P 0 ∣ \frac{|OM_0|}{|OP_0|} ∣ O P 0 ∣ ∣ O M 0 ∣ 3 5 \frac{3}{5} 5 3
tan α = y x \frac{y}{x} x y s i n α c o s α \frac{sin α}{cos α} cos α s in α 4 3 \frac{4}{3} 3 4
请根据上述任意角的三角函数定义,先将正弦、余弦、正切函数在弧度制下的定义域填入下表1.2-1,再将这三种函数的值在各象限的符号填入图1.2-6中的括号。
图1.2-6
求证:当且仅当下列不等式组成立时,角θ为第三象限角。
{ s i n θ < 0 t a n θ > 0 \begin{cases} sin θ < 0 \\ tan θ > 0 \end{cases} { s in θ < 0 t an θ > 0
**证明:**我们证明如果①②式都成立,那么θ为第三象限角。
因为①式 sin θ < 0 成立,所以θ角的终边可能位于第三或第四象限,也可能位于y轴的非正半轴上;
又因为②式 tan θ > 0 成立,所以θ角的终边可能位于第一或第三象限。
15
普通高中课程标准实验教科书 数学 4
因为①,②式都成立,所以角的终边只能位于第三象限,于是角为第三象限角。
由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等,由此得到一组公式(公式一):
sin(α+k•2π) = sin α, cos(α+k•2π) = cos α, tan(α+k•2π) = tan α, 其中k∈Z. 利用公式一,可以把求任意角的三角函数值,转化为求0到2π(或0°到360°)角的三角函数值。
(1) cos 250°;− π 4 -\frac{\pi}{4} − 4 π
解:(1)因为250°是第三象限角,所以 cos 250°<0;
(2)因为− π 4 -\frac{\pi}{4} − 4 π − π 4 -\frac{\pi}{4} − 4 π
(3)因为tan(-672°)=tan(48°-2×360°)=tan 48°,而48°是第一象限角,所以 tan(-672°)>0;
(4)因为 tan 3π=tan(π+2π)=tan π,而π的终边在x轴上,所以 tan π=0.
用计算器验证请同学们自己完成。
(1) sin 1 480°10′; (2) cos 9 π 4 \frac{9\pi}{4} 4 9 π − 11 π 6 -\frac{11\pi}{6} − 6 11 π
16
利用三角函数的定义求7 π 6 \frac{7\pi}{6} 6 7 π
已知角θ \theta θ P ( − 12 , 5 ) P(-12, 5) P ( − 12 , 5 ) θ \theta θ
填表:
角α \alpha α 0° 90° 180° 270° 360° 角α \alpha α sin α \sin\alpha sin α cos α \cos\alpha cos α tan α \tan\alpha tan α
(口答)设α \alpha α sin α \sin\alpha sin α cos α \cos\alpha cos α tan α \tan\alpha tan α tan α 2 \tan\frac{\alpha}{2} tan 2 α
确定下列三角函数值的符号:
(1) sin 156 ∘ \sin 156^\circ sin 15 6 ∘ cos 16 5 π \cos\frac{16}{5}\pi cos 5 16 π cos ( − 450 ∘ ) \cos(-450^\circ) cos ( − 45 0 ∘ )
(4) tan ( − 17 8 π ) \tan(-\frac{17}{8}\pi) tan ( − 8 17 π ) sin ( − 4 π 3 ) \sin(-\frac{4\pi}{3}) sin ( − 3 4 π ) tan 556 ∘ \tan 556^\circ tan 55 6 ∘
选择 ①sin θ > 0 \sin\theta>0 sin θ > 0 sin θ < 0 \sin\theta<0 sin θ < 0 cos θ > 0 \cos\theta>0 cos θ > 0 cos θ < 0 \cos\theta<0 cos θ < 0 tan θ > 0 \tan\theta>0 tan θ > 0 tan θ < 0 \tan\theta<0 tan θ < 0 (1) 角θ \theta θ
(2) 角θ \theta θ
(3) 角θ \theta θ
(4) 角θ \theta θ
求下列三角函数值(可用计算器): (1) cos 1109 ∘ \cos 1109^\circ cos 110 9 ∘ tan 19 π 3 \tan\frac{19\pi}{3} tan 3 19 π
(3) sin ( − 1050 ∘ ) \sin(-1050^\circ) sin ( − 105 0 ∘ ) tan ( − 31 π 4 ) \tan(-\frac{31\pi}{4}) tan ( − 4 31 π )
普通高中课程标准实验教科书 数学 4
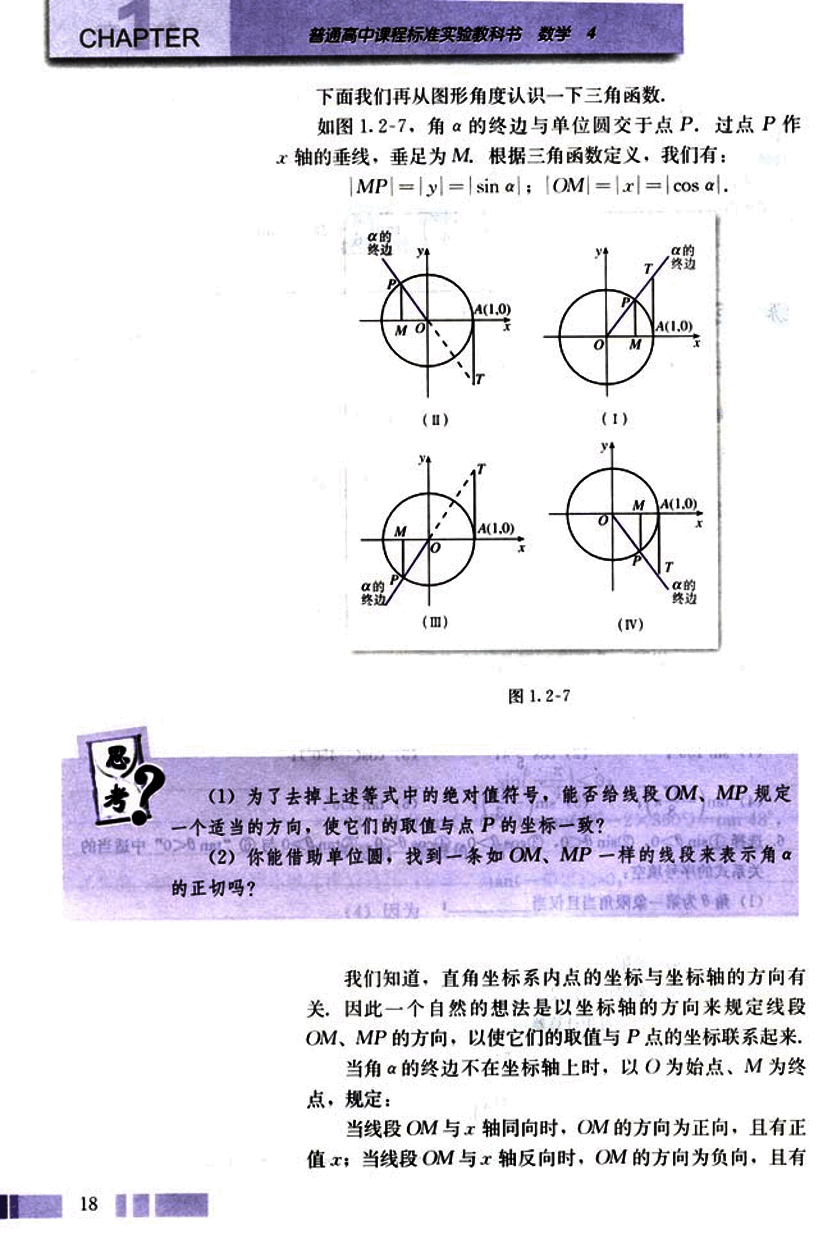
下面我们再从图形角度认识一下三角函数.
如图1.2-7. 角 α \alpha α
∣ M P ∣ = ∣ y ∣ = ∣ sin α ∣ |MP| = |y| = |\sin \alpha| ∣ MP ∣ = ∣ y ∣ = ∣ sin α ∣ ∣ O M ∣ = ∣ x ∣ = ∣ cos α ∣ |OM| = |x| = |\cos \alpha| ∣ OM ∣ = ∣ x ∣ = ∣ cos α ∣
image 图 1.2-7
思考?
(1) 为了去掉上述等式中的绝对值符号, 能否给线段 OM, MP 规定一个适当的方向, 使它们的取值与点 P 的坐标一致?
(2) 你能借助单位圆, 找到一条如 OM, MP 一样的线段来表示角 α \alpha α
我们知道, 直角坐标系内点的坐标与坐标轴的方向有关. 因此一个自然的想法是以坐标轴的方向来规定线段 OM, MP 的方向, 以使它们的取值与 P 点的坐标联系起来. 当角 α \alpha α
当线段 OM 与 x 轴同向时, OM 的方向为正向, 且有正值 x; 当线段 OM 与 x 轴反向时, OM 的方向为负向, 且有
负值x. 其中x为P点的横坐标,这样,无论哪一种情况都有
O M = x = cos α OM = x = \cos α OM = x = cos α
同理,当角α的终边不在坐标轴上时,以M为始点、P为终点,规定:
当线段MP与y轴同向时,MP的方向为正向,且有正值y;当线段MP与y轴反向时,MP的方向为负向,且有负值y.其中y为P点的纵坐标,这样,无论哪一种情况都有
M P = y = sin α MP = y = \sin α MP = y = sin α
像OM、OP这种被看作带有方向的线段,叫做有向线段(directed line segment).
那么,如何用有向线段来表示角α的正切呢?
如图 1.2-7, 过点A(1,0)作单位圆的切线,这条切线必然平行于y轴(为什么?),设它与α的终边(当α为第一、四象限角时)或其反向延长线(当α为第二、三象限角时)相交于点T.根据正切函数的定义与相似三角形的知识,借助有向线段OA、AT,我们有
tan α = A T O A = y x \tan α = \frac{AT}{OA} = \frac{y}{x} tan α = O A A T = x y
我们把这三条与单位圆有关的有向线段MP、OM、AT,分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线.
当角α的终边与x轴重合时,正弦线、正切线分别变成一个点,此时角α的正弦值和正切值都为0;当角α的终边与y轴重合时,余弦线变成一个点,正切线不存在,此时角α的正切值不存在.
你能从单位圆中的三角函数线出发得出三角函数的哪些性质? 作出下列各角的正弦线、余弦线、正切线:π 3 \frac{\pi}{3} 3 π 5 π 6 \frac{5\pi}{6} 6 5 π − 2 π 3 -\frac{2\pi}{3} − 3 2 π − 13 π 6 -\frac{13\pi}{6} − 6 13 π 作一个以5为单位长度的圆,然后分别作出225°, 330°角的正弦线、余弦线、正切线,量出它们的长度,从而写出这些角的正弦值、余弦值、正切值. 你认为三角函数线对认识三角函数概念有哪些作用? 19
三角学的起源、发展与天文学密不可分,它是天文观察结果推算的一种方法。在1450年以前的三角学主要是球面三角,这不但是因为航海、历法推算以及天文观测等人类实践活动的需要,而且也因为宇宙的奥秘对人类的巨大吸引力,这种“量天的学问”确实太诱人了。后来,由于间接测量、测绘工作的需要而出现了平面三角。
在欧洲,最早将三角学从天文学中独立出来的数学家是德国人雷格蒙塔努斯 (J. Regiomontanus, 1436–1476),他在1464年完成的5卷本的著作《论各种三角形》,是欧洲第一部独立于天文学的三角学著作。这部著作首次对三角学做出了完整、独立的阐述,前2卷论述平面三角学,后3卷讨论球面三角学。前2卷中,他采用印度人的正弦,即弧的半弦,明确使用了正弦函数,讨论了一般三角形的正弦定理,提出了求三角形边长的代数解法;后3卷中,给出了球面三角的正弦定理和关于边的余弦定理。他的工作为三角学在平面与球面几何中的应用奠定了牢固基础,对16世纪的数学家产生了极大影响,也对哥白尼等一批天文学家产生了很大影响。
由于雷格蒙塔努斯仅仅采用正弦函数和余弦函数,而且函数值也限定在正数范围内,因而不能推出应有的三角公式,导致计算的困难。后来,哥白尼的学生雷提库斯 (G. J. Rhaeticus, 1514–1576) 将传统的弧与弦的关系改进为角的三角函数关系,把三角函数定义为直角三角形的边长之比,从而使平面三角学从球面三角学中独立出来。他还采用了六个函数(正弦、余弦、正切、余切、正割、余割),制定了更为精确的正弦、正切、正割表。这些工作都极大推进了三角学的发展。实际上,由于天文学研究的需要,制定更加精确的三角函数表一直是数学家奋斗的目标,这不但大大推动了三角学的发展,而且在某种程度上还导致了对数的发明。
法国数学家韦达 (F. Vieta, 1540–1603) 所做的平面三角与球面三角系统化工作,使得三角学得到进一步发展。他总结了前人的三角学研究成果,将解平面直角三角形和斜三角形的公式汇集在一起,还补充了自己发现的新公式,如正切公式、和差化积公式等。他将解斜三角形的问题转化为解直角三角形的问题,对球面直角三角形,他给出了计算的方法和一套完整的公式及其记忆法则,并将这套公式表示成了代数形式,这是非常重要的工作。
16世纪,三角学从天文学中分离出来,成为数学的一个独立分支。后来,在微积分、物理学的研究和应用(如对振动、声音传播等的研究)中,三角学又找到了新的用武之地。
20
探
三角函数是以单位圆上点的坐标来定义的,你能从圆的几何性质出发,讨论一下同一个角的不同三角函数之间的关系吗?
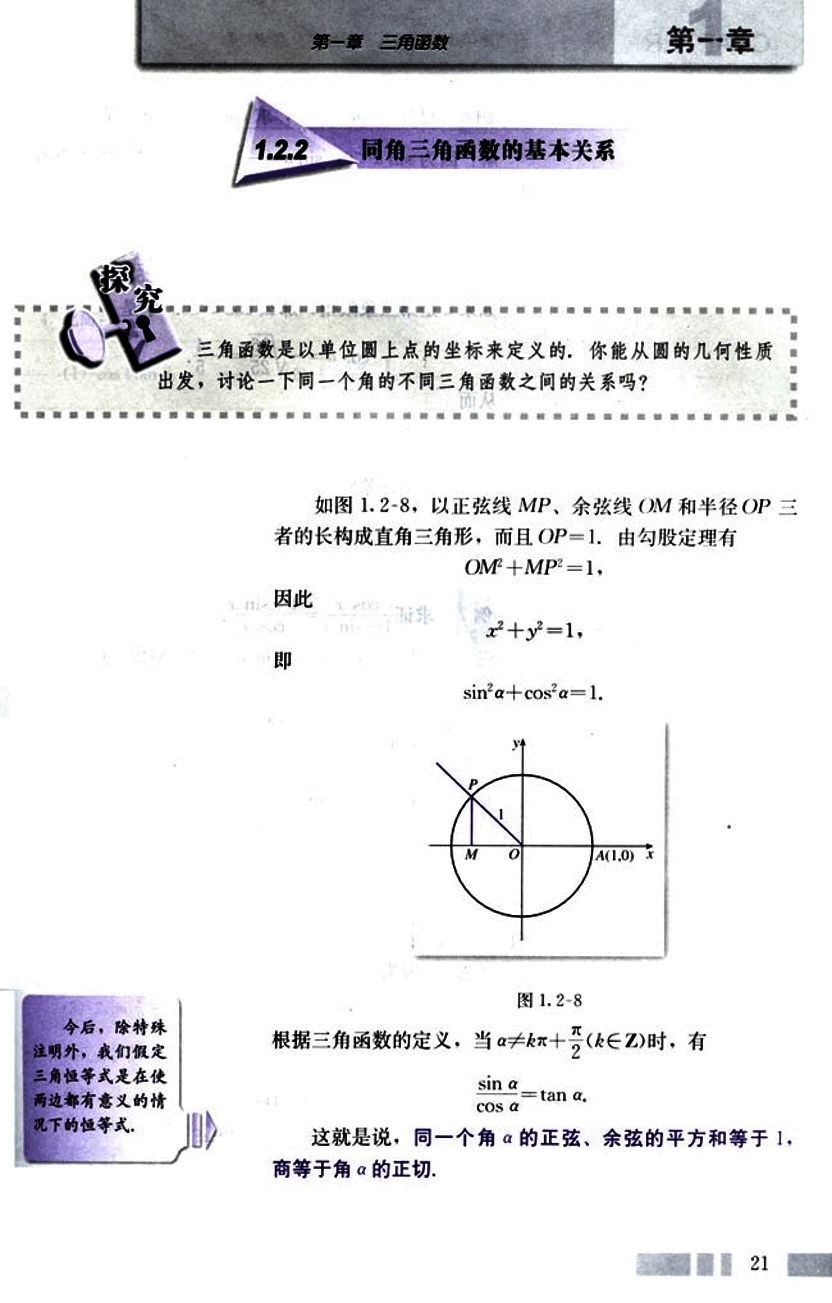
如图1.2-8,以正弦线MP、余弦线OM和半径OP三者的长构成直角三角形,而且OP=1. 由勾股定理有
因此
即
OM² + MP² = 1,
x² + y² = 1,
sin²α + cos²α = 1.
图1.2-8
今后,除特殊注明外,我们假定三角恒等式是在使两边都有意义的情况下的恒等式。
根据三角函数的定义,当α≠kπ + π/2 (k∈Z)时,有
sin α / cos α = tan α.
这就是说,同一个角α的正弦、余弦的平方和等于1,商等于α的正切。
21
普通高中课程标准实验教科书 数学 4
已知 sin a = 3 5 \sin a = \frac{3}{5} sin a = 5 3 cos a \cos a cos a tan a \tan a tan a
解:因为 sin a < 0 \sin a < 0 sin a < 0 sin a ≠ − 1 \sin a \ne -1 sin a = − 1 a a a
由 sin 2 a + cos 2 a = 1 \sin^2 a + \cos^2 a = 1 sin 2 a + cos 2 a = 1
cos 2 a = 1 − sin 2 a = 1 − ( − 3 5 ) 2 = 16 25 \cos^2 a = 1 - \sin^2 a = 1 - (-\frac{3}{5})^2 = \frac{16}{25} cos 2 a = 1 − sin 2 a = 1 − ( − 5 3 ) 2 = 25 16
如果 a a a cos a < 0 \cos a < 0 cos a < 0
cos a = − 16 25 = − 4 5 \cos a = -\sqrt{\frac{16}{25}} = -\frac{4}{5} cos a = − 25 16 = − 5 4
从而
tan a = sin a cos a = ( − 3 5 ) × ( − 5 4 ) = 3 4 \tan a = \frac{\sin a}{\cos a} = (-\frac{3}{5}) \times (-\frac{5}{4}) = \frac{3}{4} tan a = c o s a s i n a = ( − 5 3 ) × ( − 4 5 ) = 4 3
如果 a a a
cos a = 4 5 \cos a = \frac{4}{5} cos a = 5 4 tan a = − 3 4 \tan a = -\frac{3}{4} tan a = − 4 3
求证 cos x 1 − sin x = 1 + sin x cos x \frac{\cos x}{1 - \sin x} = \frac{1 + \sin x}{\cos x} 1 − s i n x c o s x = c o s x 1 + s i n x
证法 1:由 cos x ≠ 0 \cos x \ne 0 cos x = 0 sin x ≠ − 1 \sin x \ne -1 sin x = − 1 1 + sin x ≠ 0 1 + \sin x \ne 0 1 + sin x = 0
左边 = cos x ( 1 + sin x ) ( 1 − sin x ) ( 1 + sin x ) = cos x ( 1 + sin x ) 1 − sin 2 x = cos x ( 1 + sin x ) cos 2 x = 1 + sin x cos x \frac{\cos x (1 + \sin x)}{(1 - \sin x)(1 + \sin x)} = \frac{\cos x (1 + \sin x)}{1 - \sin^2 x} = \frac{\cos x (1 + \sin x)}{\cos^2 x} = \frac{1 + \sin x}{\cos x} ( 1 − s i n x ) ( 1 + s i n x ) c o s x ( 1 + s i n x ) = 1 − s i n 2 x c o s x ( 1 + s i n x ) = c o s 2 x c o s x ( 1 + s i n x ) = c o s x 1 + s i n x
所以原式成立.
证法 2:因为
( 1 − sin x ) ( 1 + sin x ) = 1 − sin 2 x = cos 2 x (1 - \sin x)(1 + \sin x) = 1 - \sin^2 x = \cos^2 x ( 1 − sin x ) ( 1 + sin x ) = 1 − sin 2 x = cos 2 x
= cos x cos x = \cos x \cos x = cos x cos x
且 1 − sin x ≠ 0 1 - \sin x \ne 0 1 − sin x = 0 cos x ≠ 0 \cos x \ne 0 cos x = 0
cos x 1 − sin x = 1 + sin x cos x \frac{\cos x}{1 - \sin x} = \frac{1 + \sin x}{\cos x} 1 − s i n x c o s x = c o s x 1 + s i n x
从例 6 可以看出,证明一个三角恒等式的方法多种多样,你能总结一下吗?
22
已知 c o s a = − 4 5 cos\ a = -\frac{4}{5} cos a = − 5 4 α \alpha α s i n α sin\ \alpha s in α t a n α tan\ \alpha t an α
已知 t a n φ = 3 tan\ \varphi = \sqrt{3} t an φ = 3 s i n φ sin\ \varphi s in φ c o s φ cos\ \varphi cos φ
已知 s i n θ = 0.35 sin\ \theta = 0.35 s in θ = 0.35 c o s θ cos\ \theta cos θ t a n θ tan\ \theta t an θ
化简:
(1) c o s θ t a n θ cos\ \theta tan\ \theta cos θt an θ
(2) 2 c o s 2 α − 1 1 − 2 s i n 2 α \frac{2cos^2\alpha - 1}{1 - 2sin^2\alpha} 1 − 2 s i n 2 α 2 co s 2 α − 1
求证: (1) s i n 4 α − c o s 4 α = s i n 2 α − c o s 2 α sin^4\alpha - cos^4\alpha = sin^2\alpha - cos^2\alpha s i n 4 α − co s 4 α = s i n 2 α − co s 2 α
(2) s i n 4 α + s i n 2 α c o s 2 α + c o s 4 α = 1 sin^4\alpha + sin^2\alpha cos^2\alpha + cos^4\alpha = 1 s i n 4 α + s i n 2 α co s 2 α + co s 4 α = 1
用定义法、公式以及计算器等求下列角的三个三角函数值: (1) − 17 π 3 -\frac{17\pi}{3} − 3 17 π 21 π 4 \frac{21\pi}{4} 4 21 π 23 π 6 \frac{23\pi}{6} 6 23 π 1500 ∘ 1500^\circ 150 0 ∘
已知角 α \alpha α s i n α sin\ \alpha s in α c o s α cos\ \alpha cos α t a n α tan\ \alpha t an α
计算:
(1) 6 s i n ( − 90 ∘ ) + 3 s i n 0 ∘ − 8 s i n 270 ∘ + 12 c o s 180 ∘ 6sin(-90^\circ) + 3sin\ 0^\circ - 8sin\ 270^\circ + 12cos\ 180^\circ 6 s in ( − 9 0 ∘ ) + 3 s in 0 ∘ − 8 s in 27 0 ∘ + 12 cos 18 0 ∘
(2) 10 c o s 270 ∘ + 4 s i n 0 ∘ + 9 t a n 0 ∘ + 15 c o s 360 ∘ 10cos\ 270^\circ + 4sin\ 0^\circ + 9tan\ 0^\circ + 15cos\ 360^\circ 10 cos 27 0 ∘ + 4 s in 0 ∘ + 9 t an 0 ∘ + 15 cos 36 0 ∘
(3) 2 c o s π 2 − t a n π 4 + 3 4 t a n 2 π 6 − s i n π 6 + c o s π 6 + s i n 3 π 2 2cos\frac{\pi}{2} - tan\frac{\pi}{4} + \frac{3}{4}tan^2\frac{\pi}{6} - sin\frac{\pi}{6} + cos\frac{\pi}{6} + sin\frac{3\pi}{2} 2 cos 2 π − t an 4 π + 4 3 t a n 2 6 π − s in 6 π + cos 6 π + s in 2 3 π
(4) s i n 2 3 π 2 + c o s 2 π 2 − t a n 2 π 3 sin^2\frac{3\pi}{2} + cos^2\frac{\pi}{2} - tan^2\frac{\pi}{3} s i n 2 2 3 π + co s 2 2 π − t a n 2 3 π
化简: (1) a s i n 0 ∘ + b c o s 90 ∘ + c t a n 180 ∘ asin\ 0^\circ + bcos\ 90^\circ + ctan\ 180^\circ a s in 0 ∘ + b cos 9 0 ∘ + c t an 18 0 ∘
23
普通高中课程标准实验教科书 数学 4
(2) − p cos 180 ∘ + q sin 90 ∘ − 2 p q cos 0 ∘ -p\cos180^\circ + q\sin90^\circ - 2pq\cos0^\circ − p cos 18 0 ∘ + q sin 9 0 ∘ − 2 pq cos 0 ∘
(3) a 2 cos 2 x − b 2 sin 2 3 π 2 + a b cos x − a b sin π 2 sin x a^2\cos2x - b^2\sin^2\frac{3\pi}{2} + ab\cos x - ab\sin\frac{\pi}{2}\sin x a 2 cos 2 x − b 2 sin 2 2 3 π + ab cos x − ab sin 2 π sin x
(4) m tan θ + n cos π 2 − p sin π − q cos 3 π 2 − r sin 2 π m\tan\theta + n\cos\frac{\pi}{2} - p\sin\pi - q\cos\frac{3\pi}{2} - r\sin2\pi m tan θ + n cos 2 π − p sin π − q cos 2 3 π − r sin 2 π
根据下列条件求函数f ( x ) = sin ( x + π 4 ) + 2 sin ( x − π 4 ) − 4 cos 2 x + 3 cos ( x + 3 π 4 ) f(x) = \sin(x + \frac{\pi}{4}) + 2\sin(x - \frac{\pi}{4}) - 4\cos2x + 3\cos(x + \frac{3\pi}{4}) f ( x ) = sin ( x + 4 π ) + 2 sin ( x − 4 π ) − 4 cos 2 x + 3 cos ( x + 4 3 π ) (1) x = π 4 x = \frac{\pi}{4} x = 4 π
(2) x = 3 π 4 x = \frac{3\pi}{4} x = 4 3 π
确定下列三角函数值的符号: (1) sin 186 ∘ \sin186^\circ sin 18 6 ∘
(2) tan 505 ∘ \tan505^\circ tan 50 5 ∘
(3) sin 7.6 π \sin7.6\pi sin 7.6 π
(4) tan ( − 23 π 4 ) \tan(-\frac{23\pi}{4}) tan ( − 4 23 π )
(5) cos 940 ∘ \cos940^\circ cos 94 0 ∘
(6) cos ( − 59 17 π ) \cos(-\frac{59}{17}\pi) cos ( − 17 59 π )
确定下列式子的符号: (1) tan 125 ∘ ⋅ sin 273 ∘ \tan125^\circ \cdot \sin273^\circ tan 12 5 ∘ ⋅ sin 27 3 ∘
(2) tan 108 ∘ \tan108^\circ tan 10 8 ∘
(3) sin 5 π 4 ⋅ cos 4 π 11 ⋅ tan 11 π 6 \sin\frac{5\pi}{4} \cdot \cos\frac{4\pi}{11} \cdot \tan\frac{11\pi}{6} sin 4 5 π ⋅ cos 11 4 π ⋅ tan 6 11 π
(4) cos 5 π 6 ⋅ tan 11 π 6 sin π 3 \frac{\cos\frac{5\pi}{6} \cdot \tan\frac{11\pi}{6}}{\sin\frac{\pi}{3}} s i n 3 π c o s 6 5 π ⋅ t a n 6 11 π
求下列三角函数值(可用计算器): (1) sin ( − 67 12 π ) \sin(-\frac{67}{12}\pi) sin ( − 12 67 π )
(2) tan ( − 15 4 π ) \tan(-\frac{15}{4}\pi) tan ( − 4 15 π )
(3) cos 398 ∘ 13 ′ \cos398^\circ13' cos 39 8 ∘ 1 3 ′
(4) tan 766 ∘ 15 ′ \tan766^\circ15' tan 76 6 ∘ 1 5 ′
求证: (1) θ \theta θ sin θ ⋅ tan θ < 0 \sin\theta \cdot \tan\theta < 0 sin θ ⋅ tan θ < 0
(2) θ \theta θ cos θ ⋅ tan θ < 0 \cos\theta \cdot \tan\theta < 0 cos θ ⋅ tan θ < 0
(3) θ \theta θ sin θ tan θ > 0 \frac{\sin\theta}{\tan\theta} > 0 t a n θ s i n θ > 0
(4) θ \theta θ sin θ ⋅ cos θ > 0 \sin\theta \cdot \cos\theta > 0 sin θ ⋅ cos θ > 0
(1) 已知sin α = − 3 2 \sin\alpha = -\frac{\sqrt{3}}{2} sin α = − 2 3 α \alpha α cos α \cos\alpha cos α tan α \tan\alpha tan α (2) 已知cos α = − 5 13 \cos\alpha = -\frac{5}{13} cos α = − 13 5 α \alpha α sin α \sin\alpha sin α tan α \tan\alpha tan α
(3) 已知tan α = − 4 3 \tan\alpha = -\frac{4}{3} tan α = − 3 4 sin α \sin\alpha sin α cos α \cos\alpha cos α
(4) 已知cos α = 0.68 \cos\alpha = 0.68 cos α = 0.68 sin α \sin\alpha sin α tan α \tan\alpha tan α
已知sin x = − 1 3 \sin x = -\frac{1}{3} sin x = − 3 1 cos x \cos x cos x tan x \tan x tan x 24
已知 tan α = √3, π < α < 3 π 2 \frac{3π}{2} 2 3 π
求证:
(1) 1 − 2 s i n x c o s x c o s 2 x − s i n 2 x = 1 − t a n x 1 + t a n x \frac{1-2sin x cos x}{cos^2 x - sin^2 x} = \frac{1-tan x}{1+tan x} co s 2 x − s i n 2 x 1 − 2 s in x cos x = 1 + t an x 1 − t an x
(2) tan²α - sin²α = tan²α sin²α;
(3) (cos β - 1)² + sin²β = 2 - 2cos β;
(4) sin²x + cos²x = 1 - 2sin x cos²x.
B 组
化简 (1 + tan²α)cos²α.
化简 1 + s i n α 1 − s i n α ⋅ 1 − s i n α 1 + s i n α \frac{\sqrt{1+sin α} }{\sqrt{1-sin α}} \cdot \frac{\sqrt{1-sin α}}{\sqrt{1+sin α}} 1 − s in α 1 + s in α ⋅ 1 + s in α 1 − s in α
已知 tan α = 2, 求 s i n α + c o s α s i n α − c o s α \frac{sin α + cos α}{sin α - cos α} s in α − cos α s in α + cos α
设 α ∈ (0, π 2 \frac{π}{2} 2 π
当 α ∈ (0, 2π) 时, 你能借助单位圆讨论一下 α 的正弦线、余弦线的数量以及长度的大小关系吗?
你能利用单位圆中的函数线, 讨论一下关系式 s i n α c o s α \frac{sin α}{cos α} cos α s in α
从本节的例 6 可以看出, c o s x 1 − s i n x = 1 + s i n x c o s x \frac{cos x}{1-sin x} = \frac{1+sin x}{cos x} 1 − s in x cos x = cos x 1 + s in x 25
37