Skip to main content

2.4　平面向量的数量积

Tong LiJanuary 23, 2025About 8 min

2.4　平面向量的数量积

128

CHAPTER 2.4 平面向量的数量积

2.4.1 平面向量数量积的物理背景及其含义

我们知道，如果一个物体在力 F\bm{F} 的作用下产生位移 s\bm{s} (图 2.4-1)，那么力 F\bm{F} 所做的功
W=∣F∣∣s∣cos⁡θ,W = |\bm{F}| |\bm{s}| \cos \theta,

其中 θ\theta 是 F\bm{F} 与 s\bm{s} 的夹角。

功是一个标量，它由力和位移两个向量来确定，这给我们一种启示，能否把“功”看成是这两个向量的一种运算的结果呢？

为此，我们引入向量“数量积”的概念，

已知两个非零向量 a\bm{a} 与 b\bm{b}，我们把数量 ∣a∣∣b∣cos⁡θ|\bm{a}| |\bm{b}| \cos \theta 叫做 a\bm{a} 与 b\bm{b} 的数量积 (inner product) (或内积)，记作 a⋅b\bm{a} \cdot \bm{b}，即

a⋅b=∣a∣∣b∣cos⁡θ,\bm{a} \cdot \bm{b} = |\bm{a}| |\bm{b}| \cos \theta,

其中 θ\theta 是 a\bm{a} 与 b\bm{b} 的夹角。∣a∣cos⁡θ|\bm{a}| \cos \theta (∣b∣cos⁡θ|\bm{b}| \cos \theta) 叫做向量 a\bm{a} 在 b\bm{b} 方向上 (b\bm{b} 在 a\bm{a} 方向上) 的投影 (projection)。如图 2.4-2，OB=∣a∣cos⁡θOB = |\bm{a}| \cos \theta。我们规定，零向量与任一向量的数量积为 0。

向量的数量积是一个数量，那么它什么时候为正？什么时候为负？

对比向量的线性运算，我们发现，向量线性运算的结果是一个向量，而两个向量的数量积是一个数量，而且这个数量的大小与两个向量的长度及其夹角有关，

图2.4-1
图2.4-2
128
129

第二章 平面向量

探究

由向量数量积的定义，你能否得到下面的结论？

设a⃗\vec{a}和b⃗\vec{b}都是非零向量，则

(1) a⃗⊥b⃗⇔a⃗⋅b⃗=0\vec{a} \perp \vec{b} \Leftrightarrow \vec{a} \cdot \vec{b} = 0

(2) 当a⃗\vec{a}与b⃗\vec{b}同向时，a⃗⋅b⃗=∣a⃗∣∣b⃗∣\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}|；当a⃗\vec{a}与b⃗\vec{b}反向时，a⃗⋅b⃗=−∣a⃗∣∣b⃗∣\vec{a} \cdot \vec{b} = -|\vec{a}| |\vec{b}|。特别地，a⃗⋅a⃗=∣a⃗∣2\vec{a} \cdot \vec{a} = |\vec{a}|^2或∣a⃗∣=a⃗⋅a⃗|\vec{a}| = \sqrt{\vec{a} \cdot \vec{a}}

(3) ∣a⃗⋅b⃗∣≤∣a⃗∣∣b⃗∣|\vec{a} \cdot \vec{b}| \le |\vec{a}| |\vec{b}|

例1

已知∣a⃗∣=5|\vec{a}| = 5，∣b⃗∣=4|\vec{b}| = 4，a⃗\vec{a}与b⃗\vec{b}的夹角θ=120∘\theta = 120^\circ，求a⃗⋅b⃗\vec{a} \cdot \vec{b}。

解：a⃗⋅b⃗=∣a⃗∣∣b⃗∣cos⁡θ\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta

=5×4×cos⁡120∘= 5 \times 4 \times \cos 120^\circ

=5×4×(−12)= 5 \times 4 \times (-\frac{1}{2})

=−10= -10

由向量投影的定义，我们可以得到a⃗⋅b⃗\vec{a} \cdot \vec{b}的几何意义：数量积a⃗⋅b⃗\vec{a} \cdot \vec{b}等于a⃗\vec{a}的长度∣a⃗∣|\vec{a}|与b⃗\vec{b}在a⃗\vec{a}的方向上的投影∣b⃗∣cos⁡θ|\vec{b}| \cos \theta的乘积。

探究

运算律和运算紧密相连，引进向量数量积后，自然要看一看它满足怎样的运算律。你能推导向量数量积的下列运算律吗？

已知向量a⃗\vec{a}，b⃗\vec{b}，c⃗\vec{c}和实数λ\lambda，则：

(1) a⃗⋅b⃗=b⃗⋅a⃗\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}；

(2) (λa⃗)⋅b⃗=λ(a⃗⋅b⃗)=a⃗⋅(λb⃗)(\lambda \vec{a}) \cdot \vec{b} = \lambda (\vec{a} \cdot \vec{b}) = \vec{a} \cdot (\lambda \vec{b})；

(3) (a⃗+b⃗)⋅c⃗=a⃗⋅c⃗+b⃗⋅c⃗(\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c}

117

129
130

CHAPTER 2

普通高中课程标准实验教科书 数学 4

下面我们证明运算律(3).

证明:如图 2.4-3, 任取一点 O, 作 OA = a, AB = b, OC = c. 因为 a + b (即 OB) 在 c 方向上的投影等于 a, b 在 c 方向上的投影的和, 即

|a + b| cos θ = |a| cos θ₁ + |b| cos θ₂ ,

|c||a + b| cos θ = |c||a| cos θ₁ + |c||b| cos θ₂ .

∴ c · (a + b) = c · a + c · b .

∴ (a + b) · c = a · c + b · c .

例 2

我们知道, 对任意 a, b ∈ R, 恒有

(a + b)² = a² + 2ab + b², (a + b)(a - b) = a² - b².

对任意向量 a, b, 是否也有下面类似的结论?

(1) (a + b)² = a² + 2a · b + b²;

(2) (a + b) · (a - b) = a² - b².

解: (1) (a + b)² = (a + b) · (a + b)

= a · a + a · b + b · a + b · b

= a² + 2a · b + b²;

(2) (a + b) · (a - b) = a · a - a · b + b · a - b · b

= a² - b².

因此, 结论是成立的.

例 3

已知 |a| = 6, |b| = 4, a 与 b 的夹角为 60°, 求

(a + 2b) · (a - 3b).

解: (a + 2b) · (a - 3b)

= a · a - a · b - 6b · b

= |a|² - a · b - 6|b|²

= |a|² - |a||b| cos θ - 6|b|²

= 6² - 6 × 4 × cos 60° - 6 × 4²

= -72.

例 4

已知 |a| = 3, |b| = 4, 且 a 与 b 不共线. k 为何值时, 向量 a + kb 与 a - kb 互相垂直?

解: a + kb 与 a - kb 互相垂直的条件是

(a + kb) · (a - kb) = 0.

130
131

第二章 平面向量

即

a2−k2b2=0.a^2 - k^2b^2 = 0.
a2=32=9,b2=42=16,a^2 = 3^2 = 9, b^2 = 4^2 = 16,
9−16k2=0.9 - 16k^2 = 0.
k=±34k = \pm \frac{3}{4}

也就是说，当k=±34k = \pm \frac{3}{4}时，a+kba + kb与a−kba - kb互相垂直.

练习

  1. 已知∣p∣=8|p| = 8, ∣q∣=6|q| = 6, pp和qq的夹角是60∘60^\circ，求p⋅qp \cdot q.
  2. 已知△ABC\triangle ABC中，AB=aAB = a，AC=bAC = b。当a⋅b<0a \cdot b < 0或a⋅b=0a \cdot b = 0时，试判断△ABC\triangle ABC的形状.
  3. 已知∣a∣=6|a| = 6, ee为单位向量，当aa，ee之间的夹角θ\theta分别等于45∘45^\circ，90∘90^\circ，135∘135^\circ时，画图表示aa在ee方向上的投影，并求其值.

2.4.2 平面向量数量积的坐标表示、模、夹角

已知两个非零向量a=(x1,y1)a = (x_1, y_1)，b=(x2,y2)b = (x_2, y_2)，怎样用aa与bb的坐标表示a⋅ba \cdot b呢？

a=x1i+y1ja = x_1i + y_1j, b=x2i+y2jb = x_2i + y_2j,
a⋅b=(x1i+y1j)⋅(x2i+y2j)a \cdot b = (x_1i + y_1j) \cdot (x_2i + y_2j)
=x1x2i⋅i+x1y2i⋅j+x2y1j⋅i+y1y2j⋅j= x_1x_2i \cdot i + x_1y_2i \cdot j + x_2y_1j \cdot i + y_1y_2j \cdot j.

又∵i⋅i=1i \cdot i = 1, j⋅j=1j \cdot j = 1,
i⋅j=j⋅i=0i \cdot j = j \cdot i = 0,

a⋅b=x1x2+y1y2a \cdot b = x_1x_2 + y_1y_2.

这就是说，两个向量的数量积等于它们对应坐标的乘积的和.

由此可得：

119

131
132

CHAPTER 2

(1)

若 a=(x,y)a=(x, y)，则 ∣a∣2=x2+y2|a|^2 = x^2 + y^2，或 ∣a∣=x2+y2|a| = \sqrt{x^2 + y^2}。

如果表示向量 a⃗\vec{a} 的有向线段的起点和终点的坐标分别为 (x1,y1)(x_1, y_1)、(x2,y2)(x_2, y_2)，那么

a⃗=(x2−x1,y2−y1)\vec{a} = (x_2 - x_1, y_2 - y_1)，

∣a∣=(x2−x1)2+(y2−y1)2|a| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}。

(2)

设 a=(x1,y1)a = (x_1, y_1)，b=(x2,y2)b = (x_2, y_2)，则

a⊥b⇔x1x2+y1y2=0a \perp b \Leftrightarrow x_1x_2 + y_1y_2 = 0。

例 5

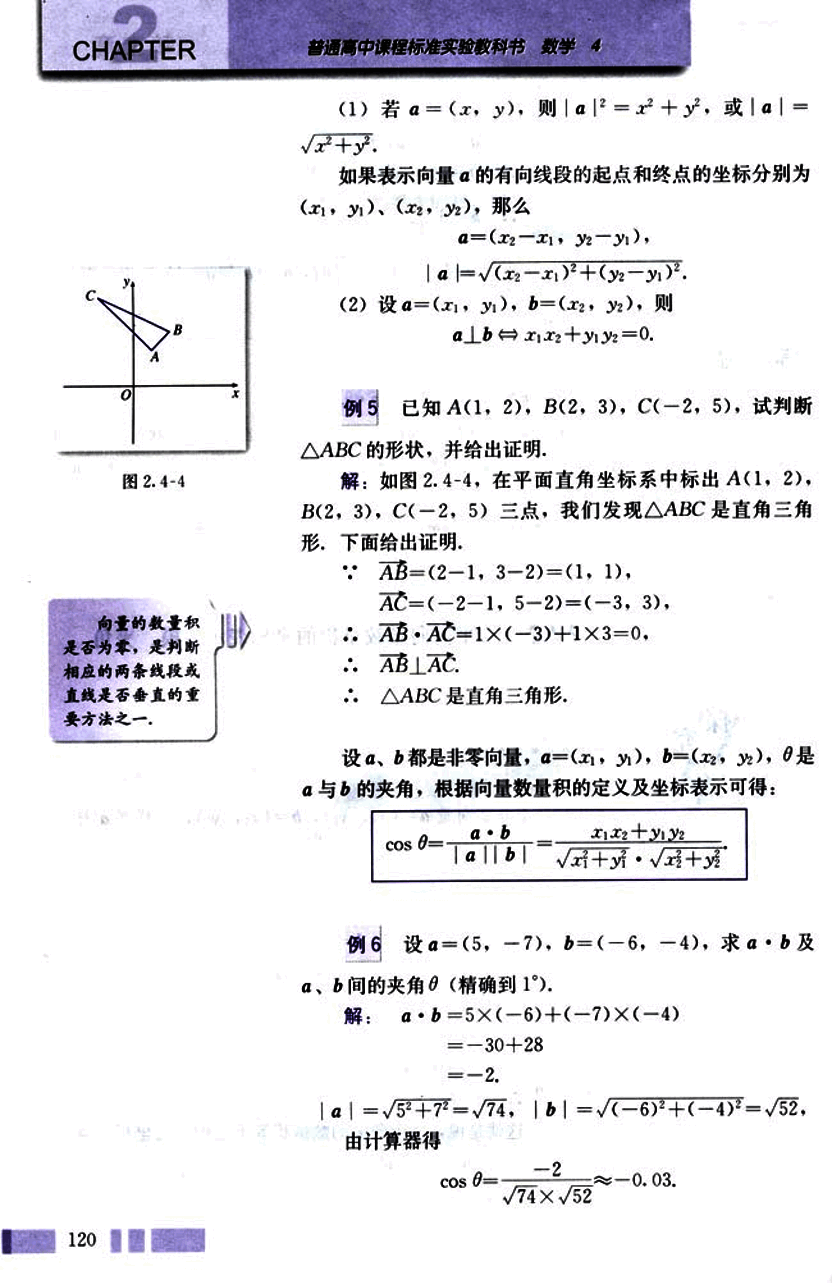
已知 A(1, 2), B(2, 3), C(-2, 5), 试判断 △ABC 的形状，并给出证明。

解：如图 2.4-4，在平面直角坐标系中标出 A(1, 2), B(2, 3), C(-2, 5) 三点，我们发现 △ABC 是直角三角形，下面给出证明。

AB⃗=(2−1,3−2)=(1,1)\vec{AB} = (2 - 1, 3 - 2) = (1, 1)，

AC⃗=(−2−1,5−2)=(−3,3)\vec{AC} = (-2 - 1, 5 - 2) = (-3, 3)，

AB⃗⋅AC⃗=1×(−3)+1×3=0\vec{AB} \cdot \vec{AC} = 1 \times (-3) + 1 \times 3 = 0，

∴AB⃗⊥AC⃗\therefore \vec{AB} \perp \vec{AC}。

∴\therefore △ABC 是直角三角形。

设 aa、bb 都是非零向量，a=(x1,y1)a = (x_1, y_1)，b=(x2,y2)b = (x_2, y_2)，θ\theta 是 aa 与 bb 的夹角，根据向量数量积的定义及坐标表示可得：

cos⁡θ=a⋅b∣a∣∣b∣=x1x2+y1y2x12+y12⋅x22+y22\cos \theta = \frac{a \cdot b}{|a||b|} = \frac{x_1x_2 + y_1y_2}{\sqrt{x_1^2 + y_1^2} \cdot \sqrt{x_2^2 + y_2^2}}

例 6

设 a=(5,−7)a = (5, -7)，b=(−6,−4)b = (-6, -4)，求 a⋅ba \cdot b 及 aa、bb 的夹角 θ\theta(精确到 1°)。

解：

a⋅b=5×(−6)+(−7)×(−4)a \cdot b = 5 \times (-6) + (-7) \times (-4)

=−30+28= -30 + 28

=−2= -2。

∣a∣=52+(−7)2=74|a| = \sqrt{5^2 + (-7)^2} = \sqrt{74}，∣b∣=(−6)2+(−4)2=52|b| = \sqrt{(-6)^2 + (-4)^2} = \sqrt{52}。

由计算器得

cos⁡θ=−274×52≈−0.03\cos \theta = \frac{-2}{\sqrt{74} \times \sqrt{52}} \approx -0.03。

120

132
133

第二章 平面向量

利用计算器中的cos⁻¹键得
θ≈1.6 rad = 92°.

练习

  1. 已知a = (-3, 4), b = (5, 2), 求|a|, |b|, a·b.
  2. 已知a = (2, 3), b = (-2, 4), c = (-1, -2), 求a·b, (a+b)·(a-b), a·(b+c), (a+b)².
  3. 已知a = (3, 2), b = (5, -7), 利用计算器, 求a与b的夹角θ(精确到1°).

习题 2.4

  1. 已知|a| = 3, |b| = 4, 且a与b的夹角θ = 150°, 求a·b, (a+b)², |a+b|.

  2. 已知△ABC中, |a| = 5, |b| = 8, C = 60°, 求BC·CA.

  3. 已知|a| = 2, |b| = 5, a·b = -3, 求|a+b|, |a-b|.

  4. 求证:
    (λα)·b = λ(a·b) = a·(λb).

  5. 先作图, 观察以A, B, C为顶点的三角形的形状, 然后给出证明:
    (1) A(-1, -4), B(5, 2), C(3, 4);
    (2) A(-2, -3), B(19, 4), C(-1, -6);
    (3) A(2, 5), B(5, 2), C(10, 7).

  6. 已知|a| = 4, |b| = 3, (2a - 3b)·(2a + b) = 61, 求a与b的夹角θ.(可用计算器)

  7. 已知|a| = 8, |b| = 10, |a + b| = 16, 求a与b的夹角θ(精确到1°).(可用计算器)

  8. 求证: A(1, 0), B(5, -2), C(8, 4), D(4, 6)为顶点的四边形是一个矩形.

  9. 已知|a| = 3, b = (1, 2), 且a//b, 求a的坐标.

  10. 已知a = (4, 2), 求与a垂直的单位向量的坐标.

  11. 设|a| = 12, |b| = 9, a·b = -54√2, 求a与b的夹角θ.(可用计算器)

121

133
134

CHAPTER

普通高中课程标准实验教科书 数学 4

B组

  1. 已知a⃗\vec{a}是非零向量，且b⃗≠c⃗\vec{b} \ne \vec{c}，求证：
    a⃗⋅b⃗=a⃗⋅c⃗⇔a⃗∥(b⃗−c⃗)\vec{a} \cdot \vec{b} = \vec{a} \cdot \vec{c} \Leftrightarrow \vec{a} \parallel (\vec{b} - \vec{c})

  2. 如图，在平面直角坐标系中，以原点为圆心，单位长度为半径的圆上有两点A(cos α, sin α), B(cos β, sin β)，试用A、B两点的坐标表示∠AOB的余弦值。

  3. 证明：对于任意的a，b，c，d∈R，恒有不等式
    (ac+bd)2≤(a2+b2)(c2+d2)(ac+bd)^2 \le (a^2+b^2)(c^2+d^2).

图1

(第2题)

(第4题)

  1. 如图，在圆C中，是不是只需知道圆C的半径或弦AB的长度，就可以求∠ABC·AC的值？

  2. 平面向量的数量积a⃗⋅b⃗\vec{a} \cdot \vec{b}是一个非常重要的概念，利用它可以容易地证明平面几何的许多命题，例如勾股定理、菱形的对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等。请你给出具体证明。

你能利用向量运算自己推导关于三角形、四边形、圆等平面图形的一些性质吗？

122

134
134
Default footer
Copyright © 2025 Tong Li