150
在章头图中,给出了这样一个问题:
某城市的电视发射塔建在市郊的一座小山上,如图 3.1-1 所示,小山高 BC 约为 30 米,在地平面上有一点 A,测得 A、C 两点间距离约为 67 米,从 A 观测电视发射塔的视角(∠CAD)约为 45°。求这座电视发射塔的高度。
设电视发射塔高 CD = x 米,∠CAB = α,则 sin α = 30 67 \sin \alpha = \frac{30}{67} sin α = 67 30
在 Rt△ABD 中,
tan ( 45 ° + α ) ≈ x + 30 60 \tan(45° + \alpha) \approx \frac{x + 30}{60} tan ( 45° + α ) ≈ 60 x + 30
如果能由 sin α = 30 67 \sin \alpha = \frac{30}{67} sin α = 67 30 tan ( 45 ° + α ) \tan(45° + \alpha) tan ( 45° + α )
能不能由 sin α = 30 67 \sin \alpha = \frac{30}{67} sin α = 67 30 tan ( 45 ° + α ) \tan(45° + \alpha) tan ( 45° + α ) sin α \sin \alpha sin α tan ( 45 ° + α ) \tan(45° + \alpha) tan ( 45° + α )
更一般地说,对于任意角 α,β,能不能用 α,β 的三角函数值把 α + β 或 α - β 的三角函数值表示出来呢?
下面我们来研究如何用任意角 α,β 的正弦、余弦值来表示 cos ( α − β ) \cos(\alpha - \beta) cos ( α − β )
图3.1-1
有兴趣的同学也可以研究用任意角 α,β 的正弦、余弦值来表示 sin ( α + β ) \sin(\alpha + \beta) sin ( α + β ) cos ( α + β ) \cos(\alpha + \beta) cos ( α + β )
138
探究
探究的过程可以分两个步骤,第一步探求表示结果,第二步对结果的正确性加以证明。
你探究得到的结果是什么呢?你认为会是cos(α-β) = cosα-cosβ吗?
不妨以特例作验证,例如,当α=60°,β=30°时,动手算一算cos 60°-cos30°的值,再与cos30°的值作比较,
容易发现cos(60°-30°)≠cos 60°-cos 30°,因此,对任意角α,β,cos(α-β)=cosα-cosβ不成立。
显然,要得到正确的结果,需要联系已学过的其他知识。
思考
由于这里涉及的是三角函数的问题,是α-β这个角的余弦问题,所以可以考虑联系单位圆上的三角函数线或向量的知识。
如图 3.1-2 ,设α的终边与单位圆的交点为P,∠POP₁=β,则∠POx=α-β。
过点P作PM垂直于x轴,垂足为M,那么OM就是角α-β的余弦线,这里就是要用角α,β的正弦线、余弦线来表示OM。
过点P作PA垂直于OP,垂足为A。过点A作AB垂直于x轴,垂足为B。过点P作PC垂直于AB,垂足为C。
139
图3.1-3
运用向量工具
那么
OA表示 cos β, AP表示 sinβ,并且∠PAC=∠POr=α,
OM = OB + BM
值得注意的是,以上结果是在α,β,α-β都是锐角,
下面再运用向量的知识进行探究,
如图3.1-3,在平面直角坐标系xOy内作单位圆,以
则 OA = (cos α, sin α), OB = (cos β, sin β).
OA · OB = |OA| · |OB| cos(α-β) = cos(α-β).
由向量数量积的坐标表示,有
OA · OB = (cos α, sin α) · (cos β, sin β)
于是
cos(α-β) = cos αcos β + sin αsin β.
思考
?
以上推导是否有不严谨之处?若有,请作出补充。
依据向量数量积的概念,角α-β必须符合条件 0 ≤ α-β ≤ π,即在此条件下,以上推导才是正确的。
由于α,β都是任意角,α-β也是任意角,因此就要研究当α-β是任意角时,以上推导是否正确的问题。
当α-β是任意角时,由诱导公式,总可以找到一个角
若θ∈[0, π],则OA·OB = cos θ = cos(α-β);
140
又由 cos β = − 5 13 \cos\beta = -\frac{5}{13} cos β = − 13 5 β \beta β
sin β = − 1 − cos 2 β = − 1 − ( − 5 13 ) 2 = − 12 13 \sin\beta = -\sqrt{1-\cos^2\beta} = -\sqrt{1-(-\frac{5}{13})^2} = -\frac{12}{13} sin β = − 1 − cos 2 β = − 1 − ( − 13 5 ) 2 = − 13 12
所以
cos ( α − β ) = cos α cos β + sin α sin β \cos(\alpha-\beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta cos ( α − β ) = cos α cos β + sin α sin β
= ( − 3 5 ) ( − 5 13 ) + ( 4 5 ) ( − 12 13 ) = (-\frac{3}{5})(-\frac{5}{13}) + (\frac{4}{5})(-\frac{12}{13}) = ( − 5 3 ) ( − 13 5 ) + ( 5 4 ) ( − 13 12 )
= 33 65 = \frac{33}{65} = 65 33
利用公式 C α − β C_{\alpha-\beta} C α − β (1) cos ( π 2 − α ) = sin α \cos(\frac{\pi}{2}-\alpha) = \sin\alpha cos ( 2 π − α ) = sin α
(2) cos ( 2 π − α ) = cos α \cos(2\pi-\alpha) = \cos\alpha cos ( 2 π − α ) = cos α
已知 cos α = − 3 5 \cos\alpha = -\frac{3}{5} cos α = − 5 3 α ∈ ( π 2 , π ) \alpha\in(\frac{\pi}{2},\pi) α ∈ ( 2 π , π ) cos ( π 4 − α ) \cos(\frac{\pi}{4}-\alpha) cos ( 4 π − α )
已知 sin θ = 15 17 \sin\theta = \frac{15}{17} sin θ = 17 15 θ \theta θ cos ( θ − π 3 ) \cos(\theta-\frac{\pi}{3}) cos ( θ − 3 π )
已知 sin α = − 2 3 \sin\alpha = -\frac{2}{3} sin α = − 3 2 α ∈ ( π , 3 π 2 ) \alpha\in(\pi, \frac{3\pi}{2}) α ∈ ( π , 2 3 π ) cos β = 3 4 \cos\beta = \frac{3}{4} cos β = 4 3 β ∈ ( 3 π 2 , 2 π ) \beta\in(\frac{3\pi}{2},2\pi) β ∈ ( 2 3 π , 2 π ) cos ( β − α ) \cos(\beta-\alpha) cos ( β − α )
由公式 C α − β C_{\alpha-\beta} C α − β
下面以公式 C α − β C_{\alpha-\beta} C α − β
142
cos ( α + β ) = cos [ α − ( − β ) ] \cos(\alpha+\beta) = \cos[\alpha-(-\beta)] cos ( α + β ) = cos [ α − ( − β )] = cos α cos ( − β ) + sin α sin ( − β ) = \cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta) = cos α cos ( − β ) + sin α sin ( − β ) = cos α cos β − sin α sin β = \cos\alpha\cos\beta - \sin\alpha\sin\beta = cos α cos β − sin α sin β C ( α + β ) C_{(\alpha+\beta)} C ( α + β ) cos ( α + β ) = cos α cos β − sin α sin β \cos(\alpha+\beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta cos ( α + β ) = cos α cos β − sin α sin β C ( α + β ) C_{(\alpha+\beta)} C ( α + β )
上面我们得到了两角和与差的余弦公式,我们知道,用诱导公式五(或六)可以实现正弦、余弦的互化,你能根据 C ( α + β ) C_{(\alpha+\beta)} C ( α + β ) C ( α − β ) C_{(\alpha-\beta)} C ( α − β ) α \alpha α β \beta β sin ( α + β ) \sin(\alpha+\beta) sin ( α + β ) sin ( α − β ) \sin(\alpha-\beta) sin ( α − β )
把结果填入下面框中:sin ( α + β ) = \sin(\alpha+\beta)= sin ( α + β ) = S ( α + β ) S_{(\alpha+\beta)} S ( α + β ) sin ( α − β ) = \sin(\alpha-\beta)= sin ( α − β ) = S ( α − β ) S_{(\alpha-\beta)} S ( α − β )
你能根据正切函数与正弦、余弦函数的关系,从 C ( ± ) C_{(\pm)} C ( ± ) S ( ± ) S_{(\pm)} S ( ± ) α \alpha α β \beta β tan ( α + β ) \tan(\alpha+\beta) tan ( α + β ) tan ( α − β ) \tan(\alpha-\beta) tan ( α − β )
143
普通高中课程标准实验教科书 数学 4
把探究的结果填入下面框中.
tan(α+β)=
tan(α-β)=
(T(α+β) )(α-β) )
公式S(α+β) ,C(α+β) ,T(α+β) 给出了任意角α,β的三角函数数值与其和角α+β的三角函数值之间的关系,为方便起见,我们把这三个公式都叫做和角公式。
类似地,S(α-β) ,C(α-β) ,T(α-β) 都叫做差角公式。
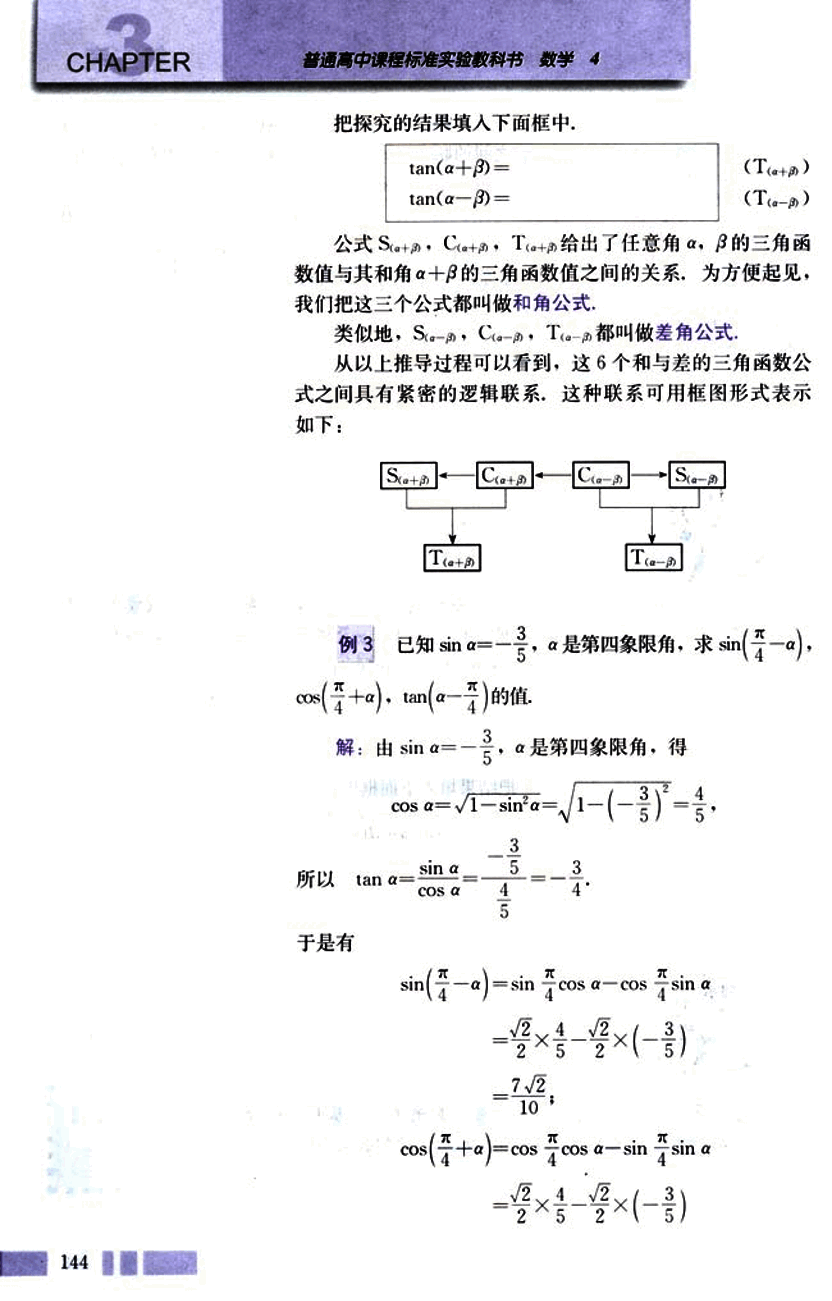
从以上推导过程可以看到,这6个和与差的三角函数公式之间具有紧密的逻辑联系,这种联系可用框图形式表示如下:
S<sub>(α+β)</sub> --> C<sub>(α+β)</sub> --> C<sub>(α-β)</sub> --> S<sub>(α-β)</sub> ↓ T<sub>(α+β)</sub> ↑ T<sub>(α-β)</sub> 例3 已知 sin α =− 3 5 -\frac{3}{5} − 5 3 π 4 \frac{\pi}{4} 4 π π 4 \frac{\pi}{4} 4 π π 4 \frac{\pi}{4} 4 π
解:由 sin α =− 3 5 -\frac{3}{5} − 5 3
cos α =1 − s i n 2 α \sqrt{1-sin^2α} 1 − s i n 2 α 1 − ( − 3 5 ) 2 \sqrt{1-(-\frac{3}{5})^2} 1 − ( − 5 3 ) 2 4 5 \frac{4}{5} 5 4
所以 tan α =s i n α c o s α \frac{sin α}{cos α} cos α s in α − 3 5 4 5 \frac{-\frac{3}{5}}{\frac{4}{5}} 5 4 − 5 3 − 3 4 -\frac{3}{4} − 4 3
于是有
sin(π 4 \frac{\pi}{4} 4 π π 4 \frac{\pi}{4} 4 π π 4 \frac{\pi}{4} 4 π
=2 2 \frac{\sqrt{2}}{2} 2 2 4 5 \frac{4}{5} 5 4 2 2 \frac{\sqrt{2}}{2} 2 2 − 3 5 -\frac{3}{5} − 5 3
=7 2 10 \frac{7\sqrt{2}}{10} 10 7 2
cos(π 4 \frac{\pi}{4} 4 π π 4 \frac{\pi}{4} 4 π π 4 \frac{\pi}{4} 4 π
=2 2 \frac{\sqrt{2}}{2} 2 2 4 5 \frac{4}{5} 5 4 2 2 \frac{\sqrt{2}}{2} 2 2 − 3 5 -\frac{3}{5} − 5 3
− 7 2 10 ; \frac{-7\sqrt{2}}{10}; 10 − 7 2 ;
tan ( a − π 4 ) = tan a − tan π 4 1 + tan a tan π 4 = tan a − 1 1 + tan a \tan(a - \frac{\pi}{4}) = \frac{\tan a - \tan \frac{\pi}{4}}{1 + \tan a \tan \frac{\pi}{4}} = \frac{\tan a - 1}{1 + \tan a} tan ( a − 4 π ) = 1 + t a n a t a n 4 π t a n a − t a n 4 π = 1 + t a n a t a n a − 1
= − 3 4 − 1 1 + ( − 3 4 ) = − 7. = \frac{-\frac{3}{4} - 1}{1 + (-\frac{3}{4})} = -7. = 1 + ( − 4 3 ) − 4 3 − 1 = − 7.
思考?
由以上解答可以看到,在本题条件下有sin ( π 4 − a ) = cos ( π 4 + a ) \sin(\frac{\pi}{4} - a) = \cos(\frac{\pi}{4} + a) sin ( 4 π − a ) = cos ( 4 π + a ) a a a
例4 利用和(差)角公式计算下列各式的值:
(1) sin 72 ∘ cos 42 ∘ − cos 72 ∘ sin 42 ∘ \sin 72^\circ \cos 42^\circ - \cos 72^\circ \sin 42^\circ sin 7 2 ∘ cos 4 2 ∘ − cos 7 2 ∘ sin 4 2 ∘
(2) cos 20 ∘ cos 70 ∘ − sin 20 ∘ sin 70 ∘ \cos 20^\circ \cos 70^\circ - \sin 20^\circ \sin 70^\circ cos 2 0 ∘ cos 7 0 ∘ − sin 2 0 ∘ sin 7 0 ∘
(3) 1 + tan 15 ∘ 1 − tan 15 ∘ \frac{1 + \tan 15^\circ}{1 - \tan 15^\circ} 1 − t a n 1 5 ∘ 1 + t a n 1 5 ∘
分析:和角与差角公式把a ± β a \pm \beta a ± β a a a β \beta β
解:(1) 由公式S a − β S_{a - \beta} S a − β
sin 72 ∘ cos 42 ∘ − cos 72 ∘ sin 42 ∘ \sin 72^\circ \cos 42^\circ - \cos 72^\circ \sin 42^\circ sin 7 2 ∘ cos 4 2 ∘ − cos 7 2 ∘ sin 4 2 ∘
= sin ( 72 ∘ − 42 ∘ ) = \sin(72^\circ - 42^\circ) = sin ( 7 2 ∘ − 4 2 ∘ )
= sin 30 ∘ = \sin 30^\circ = sin 3 0 ∘
= 1 2 = \frac{1}{2} = 2 1
(2) 由公式C a + β C_{a + \beta} C a + β
cos 20 ∘ cos 70 ∘ − sin 20 ∘ sin 70 ∘ \cos 20^\circ \cos 70^\circ - \sin 20^\circ \sin 70^\circ cos 2 0 ∘ cos 7 0 ∘ − sin 2 0 ∘ sin 7 0 ∘
= cos ( 20 ∘ + 70 ∘ ) = \cos(20^\circ + 70^\circ) = cos ( 2 0 ∘ + 7 0 ∘ )
= cos 90 ∘ = \cos 90^\circ = cos 9 0 ∘
145
普通高中课程标准实验教科书 数学 4
(3) 由公式 T ( α + β ) T_{(\alpha+\beta)} T ( α + β ) tan 45 ∘ = 1 \tan 45^\circ = 1 tan 4 5 ∘ = 1 1 + tan 15 ∘ 1 − tan 15 ∘ = tan 45 ∘ + tan 15 ∘ 1 − tan 45 ∘ tan 15 ∘ \frac{1 + \tan 15^\circ}{1 - \tan 15^\circ} = \frac{\tan 45^\circ + \tan 15^\circ}{1 - \tan 45^\circ \tan 15^\circ} 1 − t a n 1 5 ∘ 1 + t a n 1 5 ∘ = 1 − t a n 4 5 ∘ t a n 1 5 ∘ t a n 4 5 ∘ + t a n 1 5 ∘ = tan ( 45 ∘ + 15 ∘ ) = \tan (45^\circ + 15^\circ) = tan ( 4 5 ∘ + 1 5 ∘ ) = tan 60 ∘ = \tan 60^\circ = tan 6 0 ∘ = 3 = \sqrt{3} = 3
有了两角和与差的三角函数公式,我们就可以解决本章开头提出的问题了。
由 sin α = 30 67 \sin \alpha = \frac{30}{67} sin α = 67 30 cos α ≈ 60 67 \cos \alpha \approx \frac{60}{67} cos α ≈ 67 60 tan α ≈ 1 2 \tan \alpha \approx \frac{1}{2} tan α ≈ 2 1 tan ( 45 ∘ + α ) = tan 45 ∘ + tan α 1 − tan 45 ∘ tan α \tan (45^\circ + \alpha) = \frac{\tan 45^\circ + \tan \alpha}{1 - \tan 45^\circ \tan \alpha} tan ( 4 5 ∘ + α ) = 1 − t a n 4 5 ∘ t a n α t a n 4 5 ∘ + t a n α = 1 + tan α 1 − tan α = \frac{1 + \tan \alpha}{1 - \tan \alpha} = 1 − t a n α 1 + t a n α ≈ 1 + 1 2 1 − 1 2 = 3 \approx \frac{1 + \frac{1}{2}}{1 - \frac{1}{2}} = 3 ≈ 1 − 2 1 1 + 2 1 = 3
解方程 x + 30 60 = 3 \frac{x + 30}{60} = 3 60 x + 30 = 3 x = 150 x = 150 x = 150
因此这座电视发射塔的高度大约为 150 米.
利用和(差)角公式, 求下列各式的值: (1) sin 15 ∘ \sin 15^\circ sin 1 5 ∘
(3) sin 75 ∘ \sin 75^\circ sin 7 5 ∘
(2) cos 75 ∘ \cos 75^\circ cos 7 5 ∘
(4) tan 15 ∘ \tan 15^\circ tan 1 5 ∘
已知 cos θ = − 3 5 , θ ∈ ( π 2 , π ) \cos \theta = -\frac{3}{5}, \theta \in (\frac{\pi}{2}, \pi) cos θ = − 5 3 , θ ∈ ( 2 π , π ) sin ( θ + π 3 ) \sin (\theta + \frac{\pi}{3}) sin ( θ + 3 π )
已知 sin θ = − 12 13 \sin \theta = -\frac{12}{13} sin θ = − 13 12 θ \theta θ cos ( π 6 + θ ) \cos (\frac{\pi}{6} + \theta) cos ( 6 π + θ )
已知 tan α = 3 \tan \alpha = 3 tan α = 3 tan ( π 4 + α ) \tan (\frac{\pi}{4} + \alpha) tan ( 4 π + α )
146
求下列各式的值: (1) sin 72°cos 18°+cos 72°sin 18°;
(2) cos 72°cos 12°+sin 72°sin 12°;
(3) t a n 12 ° + t a n 33 ° 1 − t a n 12 ° t a n 33 ° \frac{tan 12°+tan 33°}{1-tan 12°tan 33°} 1 − t an 12° t an 33° t an 12° + t an 33°
(4) cos 74°sin 14°-sin 74°cos 14°;
(5) sin 34°sin 26°-cos 34°cos 26°;
(6) sin 20°cos 110°+cos 160°sin 70°.
化简: (1) 1 2 c o s x − 3 2 s i n x \frac{1}{2}cos x - \frac{\sqrt{3}}{2}sin x 2 1 cos x − 2 3 s in x
(2) 3 s i n x + c o s x \sqrt{3}sin x + cos x 3 s in x + cos x
(3) 2 ( s i n x − c o s x ) \sqrt{2}(sin x - cos x) 2 ( s in x − cos x )
(4) 2 c o s x − 6 s i n x \sqrt{2}cos x - \sqrt{6}sin x 2 cos x − 6 s in x
已知 sin(α-β)cos α-cos(β-α)sin α=3 5 \frac{3}{5} 5 3 β 4 + 5 π 4 \frac{\beta}{4} + \frac{5\pi}{4} 4 β + 4 5 π 以公式 C(α-β)为基础,我们已经得到六个和(差)角公式,下面将以和(差)角公式为基础来推导倍角公式。
你能利用 S i n ( α ± β ) Sin(α ± β) S in ( α ± β ) C o s ( α ± β ) Cos(α ± β) C os ( α ± β ) T a n ( α ± β ) Tan(α ± β) T an ( α ± β )
147
普通高中课程标准实验教科书 数学 4
把推导出的结果填入下列方框中:
sin 2a= (S2α )2α )2α )
在以上得到的二倍角的余弦公式 (C 2 α C_{2α} C 2 α
cos 2a=
以上这些公式都叫做倍角公式。倍角公式给出了 a 的三角函数与 2a 的三角函数之间的关系。
已知 s i n 2 a = 5 13 sin 2a = \frac{5}{13} s in 2 a = 13 5 π 4 < a < π 2 \frac{\pi}{4} < a < \frac{\pi}{2} 4 π < a < 2 π
分析: 已知条件给出了 2a 的正弦值,由于 4a 是 2a 的二倍角,因此可以考虑用倍角公式。
解: 由 π 4 < a < π 2 \frac{\pi}{4} < a < \frac{\pi}{2} 4 π < a < 2 π π 2 < 2 a < π \frac{\pi}{2} < 2a < \pi 2 π < 2 a < π
又 s i n 2 a = 5 13 sin 2a = \frac{5}{13} s in 2 a = 13 5
所以 c o s 2 a = − 1 − s i n 2 2 a = − 1 − ( 5 13 ) 2 = − 12 13 cos 2a = -\sqrt{1 - sin^2 2a} = -\sqrt{1 - (\frac{5}{13})^2} = -\frac{12}{13} cos 2 a = − 1 − s i n 2 2 a = − 1 − ( 13 5 ) 2 = − 13 12
于是
s i n 4 a = s i n [ 2 × ( 2 a ) ] sin 4a = sin[2 \times (2a)] s in 4 a = s in [ 2 × ( 2 a )] = 2 s i n 2 a c o s 2 a = 2sin 2acos 2a = 2 s in 2 a cos 2 a = 2 × 5 13 × ( − 12 13 ) = − 120 169 = 2 \times \frac{5}{13} \times (-\frac{12}{13}) = -\frac{120}{169} = 2 × 13 5 × ( − 13 12 ) = − 169 120
c o s 4 a = c o s [ 2 × ( 2 a ) ] cos 4a = cos[2 \times (2a)] cos 4 a = cos [ 2 × ( 2 a )] = 1 − 2 s i n 2 2 a = 1 - 2sin^2 2a = 1 − 2 s i n 2 2 a = 1 − 2 × ( 5 13 ) 2 = 119 169 = 1 - 2 \times (\frac{5}{13})^2 = \frac{119}{169} = 1 − 2 × ( 13 5 ) 2 = 169 119
t a n 4 a = s i n 4 a c o s 4 a tan 4a = \frac{sin 4a}{cos 4a} t an 4 a = cos 4 a s in 4 a
148
在△ABC中,cos A = 4 5 \frac{4}{5} 5 4
在△ABC中,4 5 \frac{4}{5} 5 4 1 − c o s 2 A = 1 − ( 4 5 ) 2 = 3 5 \sqrt{1 - cos^2A} = \sqrt{1 - (\frac{4}{5})^2} = \frac{3}{5} 1 − co s 2 A = 1 − ( 5 4 ) 2 = 5 3
所以 tan A = s i n A c o s A = 3 5 × 5 4 = 3 4 \frac{sin A}{cos A} = \frac{3}{5} \times \frac{5}{4} = \frac{3}{4} cos A s in A = 5 3 × 4 5 = 4 3
tan 2A = 2 t a n A 1 − t a n 2 A = 2 × 3 4 1 − ( 3 4 ) 2 = 24 7 \frac{2tan A}{1 - tan^2A} = \frac{2 \times \frac{3}{4}}{1 - (\frac{3}{4})^2} = \frac{24}{7} 1 − t a n 2 A 2 t an A = 1 − ( 4 3 ) 2 2 × 4 3 = 7 24
又 tan B = 2,
所以 tan 2B = 2 t a n B 1 − t a n 2 B = 2 × 2 1 − 2 2 = 4 − 3 \frac{2tan B}{1 - tan^2B} = \frac{2 \times 2}{1 - 2^2} = \frac{4}{-3} 1 − t a n 2 B 2 t an B = 1 − 2 2 2 × 2 = − 3 4
于是 tan(2A + 2B) = t a n 2 A + t a n 2 B 1 − t a n 2 A t a n 2 B = 24 7 + 4 − 3 1 − 24 7 × − 4 3 = 44 117 \frac{tan 2A + tan 2B}{1 - tan 2A tan 2B} = \frac{\frac{24}{7} + \frac{4}{-3}}{1 - \frac{24}{7} \times \frac{-4}{3}} = \frac{44}{117} 1 − t an 2 A t an 2 B t an 2 A + t an 2 B = 1 − 7 24 × 3 − 4 7 24 + − 3 4 = 117 44
在△ABC中,4 5 \frac{4}{5} 5 4 1 − c o s 2 A = 1 − ( 4 5 ) 2 = 3 5 \sqrt{1 - cos^2A} = \sqrt{1 - (\frac{4}{5})^2} = \frac{3}{5} 1 − co s 2 A = 1 − ( 5 4 ) 2 = 5 3
所以 tan A = s i n A c o s A = 3 5 × 5 4 = 3 4 \frac{sin A}{cos A} = \frac{3}{5} \times \frac{5}{4} = \frac{3}{4} cos A s in A = 5 3 × 4 5 = 4 3
又 tan B = 2,
所以 tan(A + B) = t a n A + t a n B 1 − t a n A t a n B = 3 4 + 2 1 − 3 4 × 2 = 11 − 2 \frac{tan A + tan B}{1 - tan A tan B} = \frac{\frac{3}{4} + 2}{1 - \frac{3}{4} \times 2} = \frac{11}{-2} 1 − t an A t an B t an A + t an B = 1 − 4 3 × 2 4 3 + 2 = − 2 11
149
− 11 2 \frac{-11}{2} 2 − 11
于是 tan ( 2 A + 2 B ) = tan [ 2 ( A + B ) ] \tan(2A+2B) = \tan[2(A+B)] tan ( 2 A + 2 B ) = tan [ 2 ( A + B )]
= tan ( A + B ) 1 − tan 2 ( A + B ) = \frac{\tan(A+B)}{1-\tan^2(A+B)} = 1 − t a n 2 ( A + B ) t a n ( A + B )
= 2 × ( − 11 2 ) 1 − ( − 11 2 ) 2 = \frac{2 \times (-\frac{11}{2})}{1-(-\frac{11}{2})^2} = 1 − ( − 2 11 ) 2 2 × ( − 2 11 )
= − 44 117 = \frac{-44}{117} = 117 − 44
已知 cos α 8 = − 4 5 \cos \frac{\alpha}{8} = -\frac{4}{5} cos 8 α = − 5 4 8 π < α < 12 π 8\pi < \alpha < 12\pi 8 π < α < 12 π sin α 4 \sin \frac{\alpha}{4} sin 4 α cos α 4 \cos \frac{\alpha}{4} cos 4 α tan α 4 \tan \frac{\alpha}{4} tan 4 α
已知 sin ( α − π ) = 3 5 \sin(\alpha - \pi) = \frac{3}{5} sin ( α − π ) = 5 3 cos 2 α \cos 2\alpha cos 2 α
已知 sin 2 α = − sin α \sin 2\alpha = -\sin \alpha sin 2 α = − sin α α ∈ ( π 2 , π ) \alpha \in (\frac{\pi}{2}, \pi) α ∈ ( 2 π , π ) tan α \tan \alpha tan α
已知 tan 2 α = 1 \tan 2\alpha = 1 tan 2 α = 1 tan α \tan \alpha tan α
求下列各式的值:
(1) sin 15 ∘ cos 15 ∘ \sin 15^\circ \cos 15^\circ sin 1 5 ∘ cos 1 5 ∘
(2) cos π 8 − sin π 8 \cos \frac{\pi}{8} - \sin \frac{\pi}{8} cos 8 π − sin 8 π
(3) tan 22.5 ∘ 1 − tan 2 22.5 ∘ \frac{\tan 22.5^\circ}{1 - \tan^2 22.5^\circ} 1 − t a n 2 22. 5 ∘ t a n 22. 5 ∘
(4) 3 tan 22.5 ∘ 2 − 2 tan 2 22.5 ∘ \frac{3 \tan 22.5^\circ}{2 - 2 \tan^2 22.5^\circ} 2 − 2 t a n 2 22. 5 ∘ 3 t a n 22. 5 ∘
150
在《数学1》的阅读与思考“对数的发明”中曾经谈到,纳皮尔利用对数制作了0°~90°每隔1′的八位三角函数表。应当说,纳皮尔仅仅凭借手工运算得到这个三角函数表的工作量是非常大的,这也显示出他超人的毅力和为科学献身的精神。今天,我们可以利用已经学会的三角函数知识以及算法知识,借助计算机,容易地制作出非常精确的三角函数表。
用科学计算器可得:
以此作为初始值,利用
cos 1′=√1-sin²1′;
就可以写出一个算法(如右图所示),然后通过计算机而得到一个正弦函数的三角函数表。
请同学们根据上述思路,自己编写程序,得出一个三角函数表。
graph TD A[开始] --> B{输入sin 1′的近似值s0}; B --> C{c0=√1-s0²}; C --> D{输出s0}; D --> E{s=s0}; E --> F{c=c0}; F --> G{n=2}; G --> H{s=s*c0+c*s0}; H --> I{c=√1-s²}; I --> J{输出s}; J --> K{n=n+1}; K --> L{n>5400?}; L -- 是 --> M[结束]; L -- 否 --> H; 151
习题 3.1
A 组
利用公式 C α C_\alpha C α S α S_\alpha S α (1) cos ( − α ) = cos α \cos(-\alpha) = \cos\alpha cos ( − α ) = cos α sin ( − α ) = − sin α \sin(-\alpha) = -\sin\alpha sin ( − α ) = − sin α
(3) cos ( π + α ) = − cos α \cos(\pi + \alpha) = -\cos\alpha cos ( π + α ) = − cos α sin ( π − α ) = sin α \sin(\pi - \alpha) = \sin\alpha sin ( π − α ) = sin α
已知 cos α = 3 5 \cos\alpha = \frac{3}{5} cos α = 5 3 0 < α < π 2 0 < \alpha < \frac{\pi}{2} 0 < α < 2 π cos ( π 6 − α ) \cos(\frac{\pi}{6} - \alpha) cos ( 6 π − α )
已知 sin α = 2 3 \sin\alpha = \frac{2}{3} sin α = 3 2 cos β = − 3 4 \cos\beta = -\frac{3}{4} cos β = − 4 3 α ∈ ( π 2 , π ) \alpha \in (\frac{\pi}{2}, \pi) α ∈ ( 2 π , π ) β ∈ ( 3 π 2 , 2 π ) \beta \in (\frac{3\pi}{2}, 2\pi) β ∈ ( 2 3 π , 2 π ) cos ( α − β ) \cos(\alpha - \beta) cos ( α − β )
已知 α \alpha α β \beta β cos α = 1 7 \cos\alpha = \frac{1}{7} cos α = 7 1 cos ( α + β ) = 11 14 \cos(\alpha + \beta) = \frac{11}{14} cos ( α + β ) = 14 11 cos β \cos\beta cos β β = ( α + β ) − α \beta = (\alpha + \beta) - \alpha β = ( α + β ) − α
已知 sin ( 30 ∘ + α ) = 3 5 \sin(30^\circ + \alpha) = \frac{3}{5} sin ( 3 0 ∘ + α ) = 5 3 60 ∘ < α < 150 ∘ 60^\circ < \alpha < 150^\circ 6 0 ∘ < α < 15 0 ∘ cos α \cos\alpha cos α
利用和(差)角公式求下列各三角函数的值:
(1) sin ( − 7 π 12 ) \sin(-\frac{7\pi}{12}) sin ( − 12 7 π ) cos ( − 61 π 12 ) \cos(-\frac{61\pi}{12}) cos ( − 12 61 π ) tan 35 π 12 \tan\frac{35\pi}{12} tan 12 35 π
已知 sin α = 2 3 \sin\alpha = \frac{2}{3} sin α = 3 2 cos β = − 3 4 \cos\beta = -\frac{3}{4} cos β = − 4 3 α ∈ ( π 2 , π ) \alpha \in (\frac{\pi}{2}, \pi) α ∈ ( 2 π , π ) β \beta β cos ( α + β ) \cos(\alpha + \beta) cos ( α + β ) sin ( α − β ) \sin(\alpha - \beta) sin ( α − β )
在 △ A B C \triangle ABC △ A BC cos A = − 12 13 \cos A = -\frac{12}{13} cos A = − 13 12 cos B = 3 5 \cos B = \frac{3}{5} cos B = 5 3 cos C \cos C cos C
已知 sin θ = 3 5 \sin\theta = \frac{3}{5} sin θ = 5 3 θ ∈ ( 0 , π 2 ) \theta \in (0, \frac{\pi}{2}) θ ∈ ( 0 , 2 π ) tan φ = 1 2 \tan\varphi = \frac{1}{2} tan φ = 2 1 tan ( θ + φ ) \tan(\theta + \varphi) tan ( θ + φ ) tan ( θ − φ ) \tan(\theta - \varphi) tan ( θ − φ )
已知 tan α \tan\alpha tan α tan β \tan\beta tan β 2 x 2 + 3 x − 7 = 0 2x^2 + 3x - 7 = 0 2 x 2 + 3 x − 7 = 0 tan ( α + β ) \tan(\alpha + \beta) tan ( α + β )
已知 tan ( α + β ) = 3 \tan(\alpha + \beta) = 3 tan ( α + β ) = 3 tan ( α − β ) = 5 \tan(\alpha - \beta) = 5 tan ( α − β ) = 5 tan 2 α \tan2\alpha tan 2 α tan 2 β \tan2\beta tan 2 β
已知 sin α = 2 3 \sin\alpha = \frac{2}{3} sin α = 3 2 cos β = − 3 4 \cos\beta = -\frac{3}{4} cos β = − 4 3 α \alpha α sin ( α + β ) \sin(\alpha + \beta) sin ( α + β )
在 △ A B C \triangle ABC △ A BC A D ⊥ B C AD \perp BC A D ⊥ BC D D D B D : D C : A D = 2 : 3 : 6 BD:DC:AD = 2:3:6 B D : D C : A D = 2 : 3 : 6 ∠ B A C \angle BAC ∠ B A C
化简:
(1) 3 15 sin x + 3 5 cos x 3\sqrt{15}\sin x + 3\sqrt{5}\cos x 3 15 sin x + 3 5 cos x
(2) 2 cos x − sin x \frac{2}{\cos x - \sin x} c o s x − s i n x 2
(3) 3 sin x + cos x \sqrt{3}\sin x + \cos x 3 sin x + cos x
(4) 2 4 sin ( π 4 − x ) + 6 4 cos ( π 4 − x ) \frac{\sqrt{2}}{4}\sin(\frac{\pi}{4} - x) + \frac{\sqrt{6}}{4}\cos(\frac{\pi}{4} - x) 4 2 sin ( 4 π − x ) + 4 6 cos ( 4 π − x )
152
(5) sin 347°cos 148°+sin 77°cos 58°
(6) sin 164°sin 224°+sin 254°sin 314°
(7) sin(α+β)cos(γ-β)-cos(γ+α)sin(β-γ)
(8) sin(α-β)sin(β-γ)-cos(α-β)cos(γ-β)
(9) tan 5 π 12 + tan 5 π 12 1 − tan 5 π 12 tan 5 π 12 \frac{\tan\frac{5\pi}{12}+\tan\frac{5\pi}{12}}{1-\tan\frac{5\pi}{12}\tan\frac{5\pi}{12}} 1 − t a n 12 5 π t a n 12 5 π t a n 12 5 π + t a n 12 5 π
(10) sin ( α + β ) − 2 sin α cos β 2 sin α sin β + cos ( α + β ) \frac{\sin(\alpha+\beta)-2\sin\alpha\cos\beta}{2\sin\alpha\sin\beta+\cos(\alpha+\beta)} 2 s i n α s i n β + c o s ( α + β ) s i n ( α + β ) − 2 s i n α c o s β
已知 sin α=0.80,α∈(0, π 2 \frac{\pi}{2} 2 π
已知 cos φ=− 3 3 -\frac{\sqrt{3}}{3} − 3 3
已知等腰三角形一个底角的正弦值为5 13 \frac{5}{13} 13 5
已知 tan α=1 7 \frac{1}{7} 7 1 1 3 \frac{1}{3} 3 1
已知 cos(α+β)cos β+sin(α+β)sin β=1 3 \frac{1}{3} 3 1 3 π 2 \frac{3\pi}{2} 2 3 π 2 α + π 4 2\alpha+\frac{\pi}{4} 2 α + 4 π
化简:
(1) (sin α+cos α)2 ^2 2
(2) cos2 ^2 2 2 ^2 2
(3) sin xcos xcos 2x
(4) 1 − tan θ 1 + tan θ \frac{1-\tan\theta}{1+\tan\theta} 1 + t a n θ 1 − t a n θ
证明: (1) sin 3α=3sin α-4sin3 ^3 3
(2) cos 3α=4cos3 ^3 3
在△ABC中,已知 tan A,tan B 是 x 的方程 x2 ^2 2
观察以下各等式:
sin$2$30°+cos$ 260 ° + s i n 30 ° c o s 60 ° = 60°+sin 30°cos 60°= 60° + s in 30° cos 60° =
sin$2$20°+cos$ 250 ° + s i n 20 ° c o s 50 ° = 50°+sin 20°cos 50°= 50° + s in 20° cos 50° =
sin$2$15°+cos$ 245 ° + s i n 15 ° c o s 45 ° = 45°+sin 15°cos 45°= 45° + s in 15° cos 45° =
分析上述各式的共同特点,写出能反映一般规律的等式,并对等式的正确性作出证明.
153
165