2.4 等比数列
2.4 等比数列
67
CHAPTER 2
2.4 等比数列
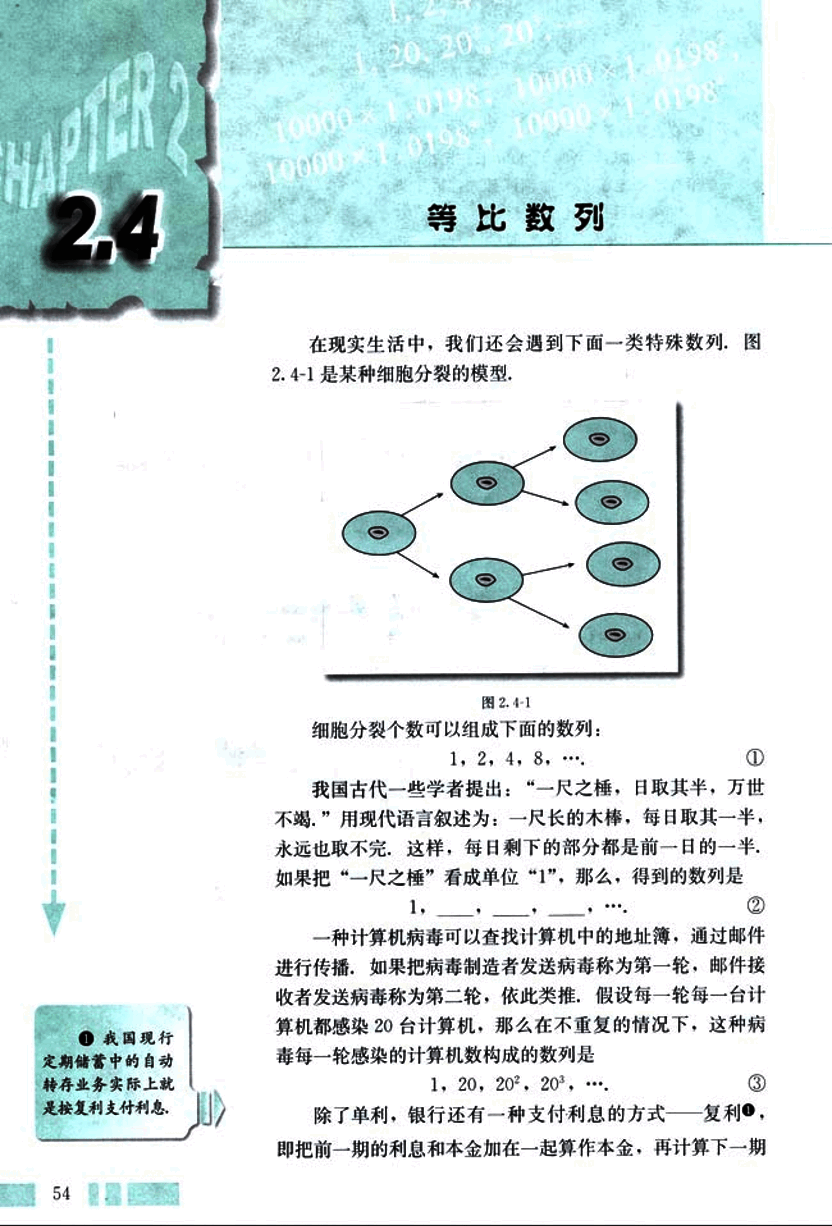
在现实生活中,我们还会遇到下面一类特殊数列,图 2.4-1 是某种细胞分裂的模型。
细胞分裂个数可以组成下面的数列:
1, 2, 4, 8, … ①
我国古代一些学者提出:“一尺之棰,日取其半,万世不竭,”用现代语言叙述为:一尺长的木棒,每日取其一半,永远也取不完,这样,每日剩下的部分都是前一日的一半,如果把“一尺之棰”看成单位“1”,那么,得到的数列是
1, ②
一种计算机病毒可以查找计算机中的地址簿,通过邮件进行传播,如果把病毒制造者发送病毒称为第一轮,邮件接收者发送病毒称为第二轮,依此类推,假设每一轮每一台计算机都感染20台计算机,那么在不重复的情况下,这种病毒每一轮感染的计算机数构成的数列是
1, 20, 202, 203, … ③
除了单利,银行还有一种支付利息的方式——复利,即把前一期的利息和本金加在一起算作本金,再计算下一期
68
第二章 数列
利滚利
的利息,也就是通常说的“利滚利”,按照复利计算本利和的公式是:
本利和=本金×(1+利率)
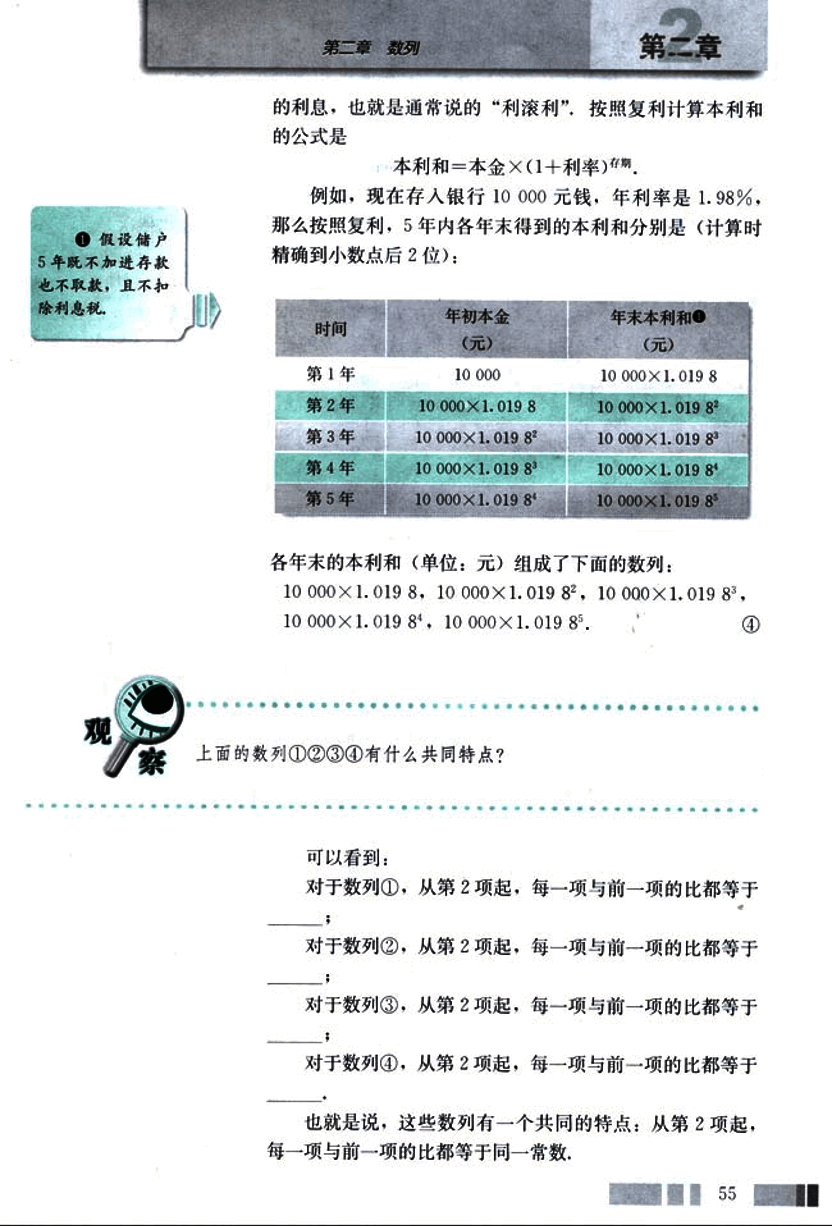
例如,现在存入银行10 000元钱,年利率是1.98%,那么按照复利,5年内各年末得到的本利和分别是(计算时精确到小数点后2位):
| 时间 | 年初本金 (元) | 年末本利和 (元) |
|---|---|---|
| 第1年 | 10 000 | 10 000×1.019 8 |
| 第2年 | 10 000×1.019 8 | 10 000×1.019 82 |
| 第3年 | 10 000×1.019 82 | 10 000×1.019 83 |
| 第4年 | 10 000×1.019 83 | 10 000×1.019 84 |
| 第5年 | 10 000×1.019 84 | 10 000×1.019 85 |
各年末的本利和(单位:元)组成了下面的数列:
10 000×1.019 8,10 000×1.019 82,10 000×1.019 83,10 000×1.019 84,10 000×1.019 85
上面的数列①②③④有什么共同特点?
可以看到:
对于数列①,从第2项起,每一项与前一项的比都等于___;
对于数列②,从第2项起,每一项与前一项的比都等于___;
对于数列③,从第2项起,每一项与前一项的比都等于___;
对于数列④,从第2项起,每一项与前一项的比都等于___;
也就是说,这些数列有一个共同的特点:从第2项起,每一项与前一项的比都等于同一个常数,
55
69
CHAPTER 2
● 一些书籍把等比数列的英文缩写记作 G. P. (Geometric Progression).
既是等差数列又是等比数列的数列存在吗?如果存在,你能举出例子吗?
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一常数,那么这个数列叫做等比数列 (geometric sequence),这个常数叫做等比数列的公比 (common ratio),公比通常用字母 表示 ().
上面的四个数列都是等比数列,公比依次是 ,,,。
与等差中项的概念类似,如果在 与 中间插入一个数 ,使 ,, 成等比数列,那么 叫做 与 的等比中项。想一想,这时 、 的符号有什么特点?你能用 与 表示 吗?
现在,我们来研究等比数列的通项公式。
(1) 写出上面四个等比数列的通项公式,类比等差数列的通项公式的推导过程,请你补全首项是 ,公比是 的等比数列 的通项公式
(2) 在右面的直角坐标系中,画出通项公式为 的数列的图象和函数 的图象,你发现了什么?
(3) 类似地,在同一直角坐标系中,画出通项公式为 的数列的图象和函数 的图象,并观察它们之间的关系。
56

70
第二章 数列
例1
●放射性物质
质衰变到原来的一
半所需时间称为这
种物质的半衰期,
某种放射性物质不断变化为其他物质,每经过一年剩留的这种物质是原来的84%。这种物质的半衰期为多长(精确到1年)?
解:设这种物质最初的质量是1,经过年,剩留量是。由条件可得,数列{}是一个等比数列,其中=0.84, =0.84.
设=0.5,则 =0.5.
两边取对数,得 0.84 = 0.5.
用计算器算得 ≈4.
答:这种物质的半衰期大约为4年。
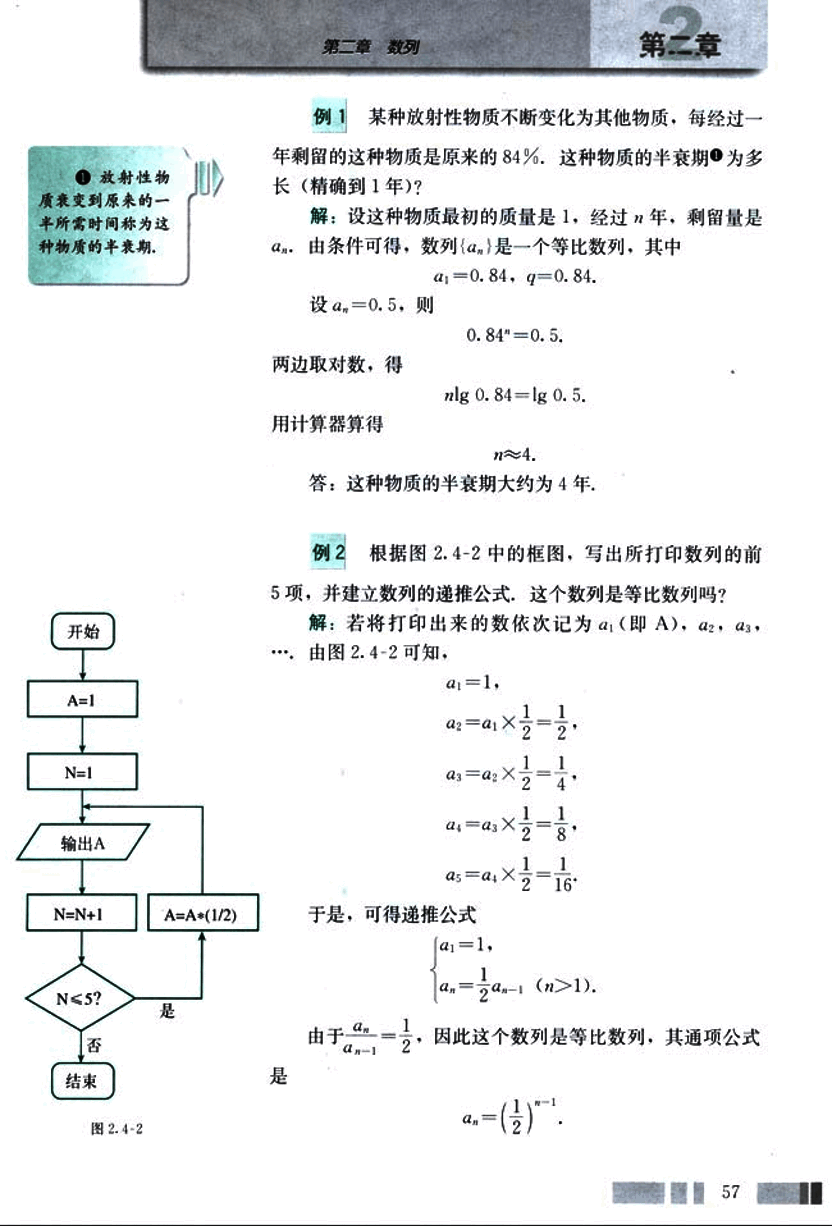
例2
根据图2.4-2中的框图,写出所打印数列的前5项,并建立数列的递推公式,这个数列是等比数列吗?
解:若将打印出来的数依次记为(即A),, ,……由图2.4-2可知,
=1,
=×=,
=×=,
=×=,
=×=.
于是,可得递推公式
=1,
(>1).
由于=,因此这个数列是等比数列,其通项公式是
=().
57
71
CHAPTER 2
例 3
一个等比数列的第 3 项和第 4 项分别是 12 和 18,求它的第 1 项和第 2 项。
解:设这个等比数列的第 1 项是 ,公比是 q,那么
①
②
② ÷ ①,得
③
把 ③ 代入 ①,得
因此,
答:这个数列的第 1 项和第 2 项分别是 与 8。
例 4
已知 , 是项数相同的等比数列,仿照下表中的例子填写表格,从中你能得出什么结论?证明你的结论。
| 判断数列 是否等比数列 | |||
|---|---|---|---|
| 例 | 是 | ||
| 自选 1 | |||
| 自选 2 |
解:填表请同学们自己完成。
根据这个表格,我们可以得到:如果 , 是项数相同的等比数列,那么 也是等比数列。
证明如下:
设数列 的公比为 p, 的公比为 q,那么数列
58

72
第二章 数列
{an•bn}的第 n 项与第 n+1 项分别为 a1pn-1•b1qn-1 与 a1pn•b1qn, 因为
,
它是一个与 n 无关的常数,所以 {anbn} 是一个以 pq 为公比的等比数列。
特别地,如果 {an} 是等比数列,c 是不等于 0 的常数,那么数列 {can} 也是等比数列。
练习
- 已知 {an} 是一个等比数列,在下表中填入适当的数:
| a1 | a3 | a5 | a7 | q |
|---|---|---|---|---|
| 2 | 2 | 8 | 0.2 |
在利用电子邮件传播病毒的例子中,如果第一轮感染的计算机数是 80 台,并且从第一轮起,以后各轮的每一台计算机都可以感染下一轮的 20 台计算机,到第 5 轮可以感染到多少台计算机?
已知 {an} 是一个无穷等比数列,公比为 q。
(1) 将数列 {an} 中的前 m 项去掉,剩余各项组成一个新的数列,这个新数列是等比数列吗?如果是,它的首项与公比分别是多少?
(2) 取出数列 {an} 中的所有奇数项,组成一个新的数列,这个新数列是等比数列吗?如果是,它的首项与公比分别是多少?
(3) 在数列 {an} 中,每隔 10 项取出一项,组成一个新的数列,这个新数列是等比数列吗?如果是,它的公比是多少?你能根据得到的结论作出一个猜想吗?
- 已知 {an} 是等比数列。
(1) 是否成立? 成立吗?为什么?
59

73
CHAPTER 2
普通高中课程标准实验教科书 数学 5
(2) (n>1) 是否成立?你据此能得到什么结论?
(n>k>0) 是否成立?你又能得到什么结论?
- 某人买了一辆价值 13.5 万元的新车,专家预测这种车每年按 10% 的速度折旧。
(1) 用一个式子表示 n (n∈N*) 年后这辆车的价值。
(2) 如果他打算用满 4 年时卖掉这辆车,他大概能得到多少钱?
习题 2.4
A 组
- 在等比数列 {an} 中,
(1) a1 = 27, q = 3, 求 a6;
(2) a5 - a1 = 15, a4 - a2 = 6, 求 a5.
某地为了保持水土资源,实行退耕还林,如果 2000 年退耕 8 万公顷,以后每年增加 10%,那么 2005 年需退耕多少公顷?(结果保留到个位)
已知 {an} 是各项均为正数的等比数列,{} 是等比数列吗?为什么?
如果能将一张厚度为 0.05 mm 的报纸对折,再对折,再对折……对折 50 次后,报纸的厚度是多少?你相信这时报纸的厚度可以在地球和月球之间建一座桥吗?
某城市今年空气质量为“良”的天数共为 105 天,力争 2 年后使空气质量为“良”的天数达到 240 天,这个城市空气质量为“良”的天数的年平均增长率为多少?(精确到小数点后 2 位)
已知 a, b 是互异的正数,A 是 a, b 的等差中项,G 是 a, b 的正的等比中项,A 与 G 有无确定的大小关系?
60

74
第二章 数列
B组
已知等比数列{}的公比为q,求证
考古学中常利用死亡的生物体中碳14元素稳定持续衰变的现象测定遗址的年代,假定碳14每年的衰变率不变,已知它的半衰期为5730年,那么:
(1) 碳14的衰变率为多少?
(2) 某动物标本中碳14的含量为正常大气中碳14含量的60%(即衰变了40%),该动物大约在距今多少年前死亡?
(第2题)
- 设任一等差数列{},计算+和+,+和+,你发现了什么一般规律,能把你发现的规律作一般化的推广吗?从等差数列和函数之间的联系角度来分析这个问题,在等比数列中会有怎样的类似结论?
61
